Введение
Многие задачи анализа геномных и протеомных данных требуют быстрой обработки большого количества длинных строк. К ним относятся, например, обнаружение мотивов (повторяющихся фрагментов в наборе последовательностей), поиск известных и предсказание новых регуляторных сайтов в последовательностях ДНК, сбор и анализ статистики по составу и расположению фрагментов в геноме или в аминокислотных последовательностях.
В Южном федеральном университете в рамках проекта «Создание биоинформационной технологии поиска взаимосвязанных сценариев организации в геномах животных и человека некодирующей ДНК и кодирующей белок ДНК» разработаны программные модули для решения ряда важный задач биоинформатики [1]. Для повышения скорости расчётов некоторые из процедур были реализованы на основе особой структуры данных – «суффиксных деревьев».
В данной статье представлено краткое описание использованных структур и результаты вычислительных экспериментов. Анализ результатов показывает, что для ряда задач применение суффиксных деревьев позволяет достичь значительного ускорения, а суффиксные деревья с ограничением глубины позволяют получить дополнительное ускорение. Однако есть задачи, для которых более эффективными оказываются «наивные» алгоритмы, не использующие суффиксные деревья.
Работа проводилась при финансовой поддержке Министерства образования и науки Российской Федерации.
Суффиксные деревья
Суффиксное дерево [1] – это структура, предназначенная для быстрой обработки больших строк (последовательностей символов в некотором алфавите). «Физически» суффиксное дерево для m-символьной строки S – это ориентированное дерево с корнем, имеющее ровно m листьев, занумерованных от 1 до m. Каждая внутренняя вершина, отличная от корня, имеет не меньше двух детей, а каждая дуга помечена непустой подстрокой строки S (дуговой меткой). Никакие две дуги, выходящие из одной и той же вершины, не могут иметь пометок, начинающихся с одного и того же символа. Главная особенность суффиксного дерева заключается в том, что для каждого листа i конкатенация меток дуг на пути от корня к листу i в точности составляет суффикс строки S, начинающийся в позиции i. Например, суффиксное дерево для строки «gatgac» имеет следующий вид (рис. 1):
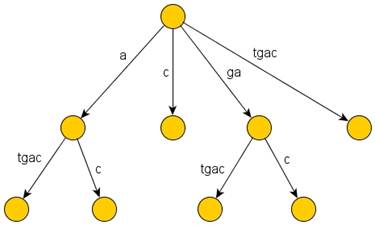
Рис. 1. Суффиксное дерево для строки «gatgac»
Для построения суффиксного дерева требуется выполнить предварительную обработку (препроцессинг) одной или нескольких обрабатываемых строк; после этого суффиксное дерево позволяет решать многие задачи очень быстро – за время, линейное от длины строки. К числу таких эффективно решаемых задач относятся задачи нахождения подстроки по заданному шаблону, наибольшей общей подстроки для нескольких строк, наибольших повторяющихся подстрок, уникальных подстрок и многие другие.
Для решения задач, связанных с поиском в наборе строк, применяются т.н. «обобщённые» суффиксные деревья, представляющие суффиксы всех строк из заданного набора.
Наиболее известные применения суффиксных деревьев связаны с исследовательскими проектами (например, проект Arabidopsis thaliana в Мичиганском университете и Университете Миннесоты и проект Saccharomyces cerevisiae (пивные дрожжи), выполняемом в Институте Макса Планка) или для решения отдельных вычислительных задач [1, 5].
Помимо перечисленных выше достоинств, применение суффиксных деревьев в процедурах обработки строк обладает и недостатками, связанными с затратами времени на препроцессинг и затратами памяти для хранения суффиксного дерева. В некоторых случаях эти дополнительные затраты могут быть сокращены за счёт применения суффиксных деревьев ограниченной глубины [5].
Дополнительные издержки на построение и хранение суффиксных деревьев приводят к тому, что в некоторых ситуациях алгоритмы, основанные на суффиксных деревьях, могут проигрывать по производительности более простым по структуре алгоритмам. Для практического применения процедур обработки длинных строк необходимо знать, для каких задач применение суффиксных деревьев действительно эффективно, а для каких задач они не дают эффекта. Результаты экспериментов вместе с описанием решаемых задач приведены в следующем разделе.
Оценка быстродействия
Для оценки выигрыша в скорости в решении биоинформационных задач при использовании суффиксных деревьев была проведена серия экспериментов. Эксперименты проводились на компьютере со следующими параметрами: процессор AMD Athlon II Neo K125, 1.70 ГГц; ОЗУ 2 Гб; ОС: Windows 7. В качестве входных данных взяты наборы случайных нуклеотидных последовательностей, сгенерированные с помощью сервиса “Random DNA sequence” на сайте “The Sequence Manipulation Suite” [6]. В качестве «модельных» были выбраны следующие задачи биоинформатики:
1) Обнаружение мотивов в наборе нуклеотидных или аминокислотных последовательностей (строк в алфавите {A, C, G, T}) с помощью частотного анализа коротких строк.
2) Картирование биологических паттернов (в т.ч. факторов транскрипции) для заданного набора последовательностей. Алгоритмически задача сводится к поиску вхождений коротких строк (паттернов) из заданного набора в длинных строках из другого набора.
3) Поиск потенциальных «шпилек» (палиндромов).
Каждая из задач решалась тремя способами:
· «Наивным» алгоритмом, основанном на сканировании длинных строк и проверки всех подстрок на соответствие критериям поиска.
· Поиск по полному суффиксному дереву.
· Поиск по суффиксному дереву ограниченной глубины.
Обнаружение мотивов
Входные данные:
· Набор последовательностей (строк в алфавите {A,C,G,T}) S = {S1, …, Sn}, объединённых функционально или эволюционно.
· Контрольный набор последовательностей: C = {C1, …, Cm}.
Задача заключается в том, чтобы найти мотивы – строки длины от Lmin до Lmax, каждая из которых входит как минимум в QS последовательностей из S и не более чем в QC последовательностей из C. Вхождение мотива в строку определяется с точностью до K замен символов.
Результаты численных экспериментов продемонстрированы на рис. 2 и рис.3. Формат диаграмм: ось абсцисс – количество последовательностей, ось ординат – время выполнения процедуры, в миллисекундах.
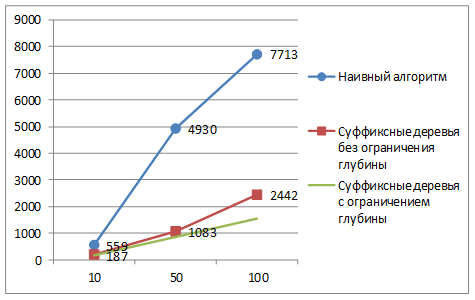
Рис. 2. Время обнаружения мотивов. Длина каждой последовательности: 1 000
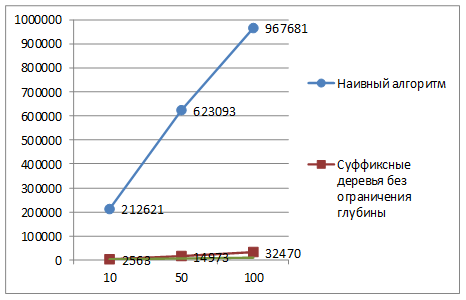
Рис. 3. Время обнаружения мотивов. Длина каждой последовательности: 10 000
Анализ показывает, что наибольший выигрыш от применения суффиксных деревьев достигается при обработке большого количества последовательностей (чем больше последовательностей, тем больше выигрыш).
Поиск набора паттернов
Дано:
· Набор последовательностей (строк) S = {S1, …, Sn}.
· Набор паттернов P = {P1, …, Pm}.
Задача: для каждого паттерна найти все его вхождения во все заданные последовательности, с точностью до K замен символов.
Результаты численных экспериментов для набора паттернов длины 6 продемонстрированы на рис. 4. Формат диаграмм: ось абсцисс – количество паттернов, ось ординат – время выполнения процедуры, в миллисекундах.
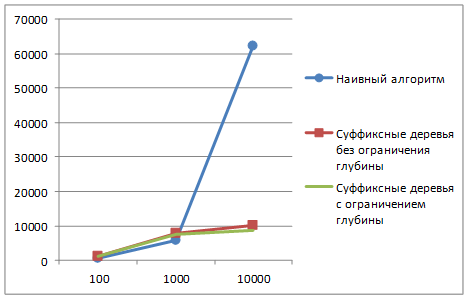
Рис. 4. Время на поиск паттернов длины 6
Вывод: наибольший выигрыш от применения суффиксных деревьев достигается при поиске большого набора относительно коротких паттернов.
Обнаружение палиндромов
Определение: палиндромом (более точное название – «комплементарный палиндром») называется фрагмент последовательности ДНК, который совпадает со своим обратным комплементарным фрагментом. Пример палиндрома: “TTTTAAAA”.
Задача: для заданной строки найти все палиндромы длины от Lmin до Lmax с точностью до K замен.
Обнаружение палиндромов представляет важную задачу анализа ДНК, поскольку такие участки способны образовывать «шпильки» (англ. hairpin), участвующие в регуляции транскрипции ДНК.
В программный модуль была включена процедура, находящая все максимальные палиндромы с помощью суффиксных деревьев [1].
Численные эксперименты показали, что для данной задачи применение суффиксных деревьев не даёт выигрыша в скорости счёта (рис. 5). Формат диаграммы на рис. 5: ось абсцисс – длина строки, ось ординат – время выполнения процедуры, в миллисекундах
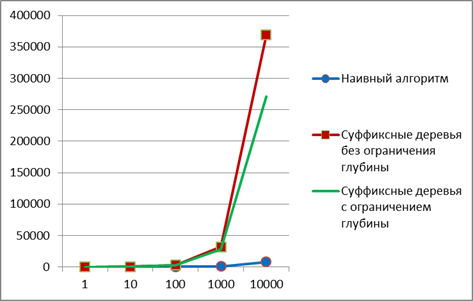
Рис. 5. Время на поиск палиндромов
Более детальный анализ показал, что причина этого в том, что при решении данной задачи каждая строка обрабатывается отдельно, а длина палиндромов обычно невелика. Поэтому применение «наивного» алгоритма даёт в среднем достаточную скорость вычислений, а алгоритмы, построенные на основе суффиксного дерева, вынуждены тратить много времени на построение дерева для каждой анализируемой последовательности.
Заключение
Результаты анализа показывают, что суффиксные деревья позволяют достичь значительного ускорения при решении задач, в которых требуется выполнять многочисленные сравнения различных строк с одной и той же строкой – такова ситуация с обнаружением мотивов и поиском паттернов. Вместе с тем для анализа одной строки (задача обнаружения палиндромов) более эффективен «наивный» подход, не требующий дополнительных затрат на построение вспомогательных структур данных.
Рецензенты:
Ильичев Виталий Григорьевич, докт. техн. наук, главный научный сотрудник, Учреждение Российской академии наук, Институт аридных зон Южного научного центра, г. Ростов-на-Дону.
Чернов Андрей Владимирович, заведующий кафедрой «Прикладной математики и вычислительной техники», докт. техн. наук, доцент, ФГБОУ ВПО «Ростовский государственный строительный университет» (РГСУ), г. Ростов-на-Дону.



