Введение
Проблема оптимизации формирования информационного базиса (ИБ) в интерактивных адаптивно-обучающих системах, проектируемых на основе современных принципов построения моделей курсов, позволяющих унифицировать требования к их блочно-модульной структуре, последовательности представления компонентов ИБ учебно-методических материалов (УММ), упаковке курсов в уникальные оболочки и среды, является в настоящее время актуальной [3; 4]. В данной работе исследуется зависимость общей трудоемкости прохождения курса от степени дробления его ИБ УММ на блоки и сборки их в модули УММ. Целью работы является синтез оптимальной по трудоемкости освоения структуры ИБ для интерактивных систем обучения.
Материал и методы
Следуя часто используемой дидактической модели процесса интерактивного освоения ИБ УММ, можно принять гипотезу об экспоненциальном характере зависимости вероятности успешного прохождения контрольных мероприятий от объема базиса. Если объем информационного материала некоторого базиса составляет Q часов, то вероятность успешного выполнения контрольных мероприятий может быть представлена в виде:
, (1)
где l (1/час) – константа, показывающая скорость снижения вероятности успешного завершения процесса освоения материала информационного базиса УММ в зависимости от его объема.
Зависимость (1) соответствует интуитивному представлению об успешности процесса прохождения интерактивного курса. Если объем информационного базиса мал (Q®0), то вероятность освоения этого базиса стремится к единице, а если он весьма велик (Q®¥), то вероятность его освоения стремится к нулю. Величина l зависит от вида (содержательного, структурного и т.п.) базиса, она может быть оценена экспертно или экспериментально на основе опыта работы с определенным видом информационно-терминологических базисов.
Рассмотрим цепь Маркова [5], описывающую вероятностный процесс изучения отдельного модуля информационного базиса УММ (рис. 1).
В данной модели выделены следующие состояния: S1 – изучение теоретического материала ИБ УММ; S2 – получение справок и консультаций при изучении теоретического материала; S3 – выполнение контрольных мероприятий; S4 – завершение изучения модуля ИБ УММ.
Зададим вероятности переходов из одного состояния в другое: r – вероятность обращения за справками или консультациями при изучении УММ интерактивного курса; s – вероятность перехода к контрольным мероприятиям; p – вероятность успешного выполнения контрольных мероприятий и завершения освоения модуля курса; q – вероятность неудачи при выполнении контрольных мероприятий и повторного изучения модуля.
В рассматриваемой схеме выполняются очевидные соотношения:
r+s=1, p+q=1. (2)
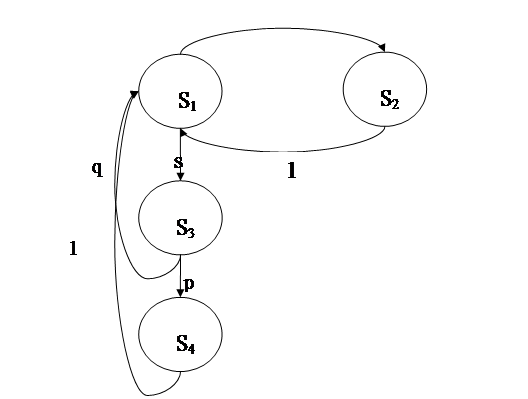
Рис. 1. Модель вероятностного процесса изучения отдельного модуля ИБ УММ
Матрица вероятностей переходов между состояниями:
s1 s2 s3 s4
P= 
.
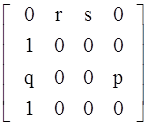Выделим в P матрицу вероятностей переходов между состояниями невозвратного множества и обозначим Q.
s1 s2 s3
Q=
.
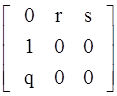Тогда матрица среднего числа пребываний процесса в состояниях невозвратного множества определяется по формуле:
,
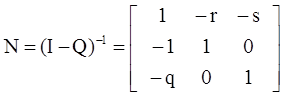где I – единичная матрица размерности 3´3.
Поскольку процесс всегда стартует из состояния Si, нам достаточно определить только первую строчку матрицы N; ее элементы обозначим n1,…,n4. Проделав вычисления обратной матрицы 
, получим оценки среднего числа попыток изучения всех компонентов информационного базиса УММ – среднее число пребываний процесса соответственно в состояниях {S1,…,S4} при старте из состояния S1:
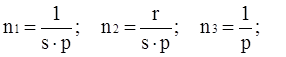(3)
при этом здесь n1 – среднее число попыток изучения информационного материала; n2 – среднее число обращений за справками и консультациями при изучении информационного материала; n3 – среднее число попыток выполнения контрольных мероприятий.
Обозначим трудоемкости изучения всех компонентов информационного базиса УММ (в часах): Q – трудоемкость изучения информационного материала; Q1 – трудоемкость получения справок и консультаций при изучении информационного материала (состояние S2); Q2 – трудоемкость выполнения контрольных мероприятий (состояние S3).
Суммарная трудоемкость прохождения информационного базиса УММ с учетом (3) определяется выражением:
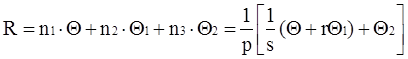. (4)
Рассмотрим оценки параметров, входящих в формулу (4). Вероятность r определяются экспертно или на основе обработки протоколов прохождения интерактивных учебных курсов. Вероятность p определяется формулой (2). Трудоемкость Q определяется объемом учебного курса, для которого формируется ИБ УММ, трудоемкость Q1 может быть взята как некоторая доля величины Q:
Q1=k1Q, (5)
где k1<1 – доля затрат на получение справок и консультаций, определяемая экспертно или на основе статистики. Трудоемкость Q2 может быть представлена как сумма постоянной и переменной составляющих:
Q2=m+k2Q, (6)
где m (часов) – трудоемкость работы по выполнению контрольных мероприятий, не зависит от размеров ИБ УММ; k2<1 – доля затрат на выполнение контрольных мероприятий.
В результате подстановки значений параметров (5), (6) формула (4) приобретет вид:
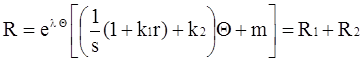, (7)
причем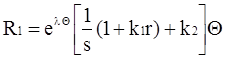 
– затраты на изучение ИБ УММ;
– затраты времени на выполнение контрольных мероприятий. Обозначим:
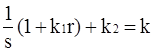. (8)
С учетом (8) выражение для суммарной трудоемкости (7) упростится
. (9)
Рассмотрим задачу разбивки некоторого информационного базиса УММ с общим объемом материала Q часов на n модулей [1], каждый из которых имеет объем Qi часов:
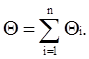(10)
Трудоемкость изучения каждого модуля в соответствии с (9) составит:
, (11)
а общая трудоемкость освоения базиса:
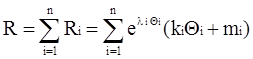. (12)
Рассмотрим предельные случаи. При n = 1 получаем формулу (9). При n®¥ Qi®0, exp(liQi)®1, и из (12) следует, что R®¥. Таким образом, функция R имеет, по крайней мере, один минимум.
Выбирая количество модулей n и их объем Qi, можно добиться наименьшей общей трудоемкости освоения модульной структуры ИБ УММ. Математически эта задача формулируется следующим образом: задан критерий (12) при условиях (10). Требуется найти такие n и {Q1,…,Qn}, чтобы обеспечить оптимальные значения критерия (12):
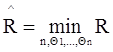. (13)
Задача (13) представляет собой задачу оптимизации нелинейного критерия при ограничениях на переменные. В аналитическом виде эта задача решается достаточно сложно, а численно может быть решена путем перебора вариантов разбивки базиса УММ на модули.
Результаты
Наличие экспоненциальных множителей в выражении (12) говорит о том, что лучших результатов можно ожидать, если величины li и Qi будут равны между собой. Рассмотрим задачу о разбивке базиса на модули, равновеликие по объему изучаемого материала.
Положим, что Qi=Q/n, i=1,…,n, т.е., что все модули имеют одинаковый объем, кроме того, они все имеют одинаковые параметры li=l, ki=k, mi=m. Тогда критерий (12) примет вид:
(14)
и единственным параметром оптимизации становится n.
Для получения оптимального значения n необходимо решить относительно n уравнение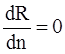 
или, с учетом (14),
.
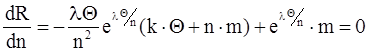Отсюда после некоторых преобразований получаем квадратное уравнение относительно n:
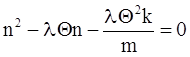. (15)
Оптимальное значение 
определяется положительным корнем уравнения (15):
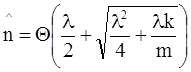. Величина 
определяет оптимальный размер модуля ИБ УММ.
Рассмотрим еще одну практически важную разновидность задачи синтеза структуры информационного базиса для интерактивных систем обучения. Пусть информационно терминологический базис состоит из множества априори заданных блоков 
Каждый блок Si характеризуется параметрами: Qi – объем информационного материала блока ИБ, час; mi – трудоемкость организации контрольных мероприятий, час; li – коэффициент сложности, 1/час; ki – коэффициент увеличения трудоемкости. Кроме того, для каждой пары блоков 
установлен порядок их изучения: отношение Si®Sj означает, что блок Si должен быть изучен раньше блока Sj, а отношение Si=Sj означает, что эти блоки могут изучаться в произвольном порядке.
Задача заключается в следующем: указанные блоки должны быть скомплектованы в модули таким образом, чтобы трудоемкость освоения интерактивного курса в целом была бы минимальной. Каждый модуль может включать один или несколько блоков, причем упорядоченность блоков должна сохраняться как внутри каждого модуля, так и в целом по базису. Требуется сформировать т модулей (т априори неизвестно), каждый из которых содержит множество блоков 
причем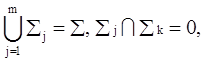 
при j≠k. Первое равенство в этом выражении означает, что должны быть использованы все блоки, а второе – что разные модули не должны содержать одинаковые блоки.
Характеристики каждого модуля определяются на основе характеристик, вошедших в него блоков:
.
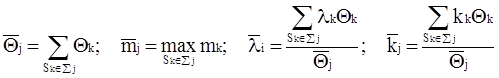Трудоемкость изучения j-го модуля определяется ранее полученной формулой (11):
, а общая трудоемкость в соответствии с (12) равна:
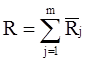. Этот показатель должен быть минимизирован за счет числа и состава модулей, т.е.
.
Данную задачу с помощью компьютера можно решить полным перебором, однако, на задачах с количеством блоков, большим 8, время решения становится очень большим. Решение данной задачи аналитическим путем является крайне сложным, поэтому для нахождения псевдо-оптимального решения используются алгоритмы случайного поиска [2].
Выводы
В результате данной работы сформулированы задачи определения оптимальной структуры информационного базиса, получено их решение для случаев равномерной разбивки базиса и его синтеза из заданных блоков. Предложены алгоритмы решения задач определения оптимальной по трудоемкости освоения блочно-модульной структуры информационного базиса для случаев равномерной разбивки базиса и его синтеза из заданных блоков.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Антамошкин Александр Николаевич, д-р техн. наук, профессор, профессор кафедры системного анализа и исследования операций СибГАУ, г. Красноярск.
Ходос Дмитрий Васильевич, д-р экон. наук, доцент, профессор кафедры экономики и информационных технологий менеджмента СФУ, г. Красноярск.
Кирьянов Борис Фёдорович, д.т.н., профессор, профессор кафедры прикладной математики и информатики, ФГБОУ ВПО Новгородский государственный университет им. Ярослава Мудрого, г. Великий Новгород.