Ю.С. Осиповым и А.В. Кряжимским в [4] предложен динамический подход, позволяющий в режиме реального времени восстанавливать неизвестное управление 
в системе вида
(1)
по неточной информации 
о движении системы 
(
– евклидова норма,
), доступной в узлах
временного промежутка
.
Предполагается, что 
и 
– отображения: 
в 
и в пространство матриц размерности 
со спектральной нормой (
), соответственно; при 
значения измеримой функции u(t) принадлежат выпуклому компакту 
каждое значение x(t) является внутренней точкой компакта 
Известно, что в общем случае эта задача является некорректной, поскольку множество управлений, порождающих конкретное движение, вообще говоря, неодноэлементно. Упомянутый выше подход основан на идее стабилизации аналога функционала А.Н. Тихонова с помощью процедуры экстремального прицеливания, введенной Н.Н. Красовским в теории позиционных дифференциальных игр, и его специфика состоит в том, что он позволяет восстанавливать нормальное управление 
– управление, обладающее минимальной нормой в 
, среди всех управлений, порождающих наблюдаемое движение, в режиме реального времени.
Формально реализация алгоритма состоит из следующих этапов.
1. До начала работы задается разбиение промежутка и выбираются величины: 
, 
(далее для простоты полагаем 
), 
, 
, и значение 
, полагается равным проекции нуля на компакт Q.
2. На каждом шаге 
вычисляется:
а) состояние 
системы модели, функционирующей по правилу
;
б) значение 
– результат проекции на Q вектора 
.
Таким образом, формируется приближение в виде кусочно-постоянной функции 
при 
. Описанный выше алгоритм 
получил название метода динамической регуляризации. В цитируемой работе доказано следующее.
Утверждение 1. Пусть 
удовлетворяют условию Липшица по совокупности переменных с общей константой L; 
согласуются так, что величина 
стремится к нулю вместе с h. Тогда 
является 
нормально регуляризирующим, то есть 
Введем вспомогательные понятия.
Определение 1. Функция 
называется нижней (верхней) оценкой точности
алгоритма в функциональном пространстве F, если существует 
такое, что для всех
имеет место неравенство 
.
Определение 2 . Функцию 
назовем порядком точности при уровне погрешности 
, если существуют 
такие, что 
, а число 
– асимптотическим порядком точности.
В работе [3] получены верхние и нижние оценки точности 
– модификации исходного алгоритма , позволяющей отказаться от трудоемкой процедуры проектирования на компакт при построении 
, в метрике пространства 
.
Утверждение 2. Пусть: 1) ранг матрицы 
постоянен, вариация 
ограничена при 
; 2) значения являются внутренними точками соответствующего компакта 
; 3) компакт содержит 0; 4) существует 
такое, что для всех 
величины 
, 
ограничены. Тогда при выборе параметров 
, 
асимптотический порядок точности в пространстве 
равен ½.
Возможность получения асимптотического порядка точности в равномерной метрике (
) для 
рассматривалась в [5].
Утверждение 3. Пусть: 1) выполнены условия утверждения 2; 2) 
удовлетворяет условию Липшица на ; 3) известно 
такое, что 
, 
. Тогда при выборе параметров , , 
асимптотический порядок точности в равномерной метрике равен ½, то есть порядок точности данного алгоритма является асимптотически оптимальным.
Поскольку известно, что нижняя оценка точности в равномерной метрике удовлетворяет условию 
, то цель работы состоит в получении верхней оценки точности в равномерной метрике на промежутке 
. Пусть задано точное начальное условие 
, тогда согласно подходу, предложенному в [5], система (1) при выборе 
,
может быть приведена к виду
(2)
Выполнение условий утверждения 3 гарантирует существование положительных констант Mf, Mg, Mv таких, что 
, 
. Через Lv обозначим константу Липшица нормального управления 
. При отказе от проектирования на компакт, постоянное приближение 
управления 
на каждом шаге определяется следующим образом: 
Зафиксируем . Управление 
и систему – модель
(3)
где 
назовем виртуальными. Для получения асимптотического порядка точности оценим сначала 
, а затем норму разности 
. Если предположить невырожденность матрицы коэффициентов при управлении вдоль наблюдаемой траектории, то подход, предложенный в [2] для получения оценки первой из указанных норм, может быть использован и в случае бесконечного временного промежутка:
решение задачи Коши (3) представим в виде
(4)
где 
– решение дифференциального уравнения
(5)
с начальным условием 
(E – единичная матрица). Интегрирование по частям от a до t второго слагаемого из правой части (4), с учетом (2) и (5), приводит к равенству
В силу свойств обратной матрицы, с учетом дифференциального уравнения (5), имеем:
(6)
Обозначим 
. Введем понятие оператора восстановления значения F(t). Пусть 
, 
, 
и 
.
Рассмотрим представление 
Интегральный оператор в левой части последнего равенства назовем оператором восстановления значения 
, 
– погрешностью, а 
его ядром.
Утверждение 4. [3] Пусть выполнены условия утверждения 3. Тогда существует h1>0 такое, что для всех 
, 
, 
имеет место оценка 
, где 
точная нижняя грань на минимального собственного числа
матрицы 
.
Несложно убедиться в результатах лемм 1, 2.
Лемма 1. Если матрица 
, отображение 
удовлетворяет условию Липшица с константой Lp и для всех 
справедливы оценки 
,
, то 
.
Лемма 2. Пусть выполнены условия утверждения 3, матрица 
обратима на промежутке 
. Тогда F(t) удовлетворяет условию Липшица с константой 
, равной 
.
Лемма 3. Пусть выполнены условия утверждения 3; 
стремятся к нулю вместе с h, 
при 
, и 
. Тогда существуют 
такие, что для всех 
погрешность оператора восстановления значения F(t) удовлетворяет оценке: 
где 
выписываются конструктивно.
Доказательство. Пусть 
при 
, определим
, 
,
.
Оценим каждую из указанных величин. В силу утверждения 4, дифференциального уравнения (5) для 
справедливо:
Для получения оценки 
воспользуемся результатами лемм 1, 2:
Для 
, с учетом начального условия:
Тогда 
где 
, 
.
Заметим, что для любого
можно указать 
такое, что для всех справедливо 
из которого следует требуемый результат.
Следствие. В силу (6), ограниченности 
и утверждения 4 существует 
такая, что для всех имеет место неравенство 
.
Лемма 4. Пусть выполнены условия леммы 3. Тогда существуют 
, 
такие, что для всех справедлива оценка 
Доказательство. В силу леммы 3 и равенства (6):
,
из этого следует существование 
, по норме меньшего единицы такого, что
.
Разрешая последнее уравнение относительно 
, получаем:
,
поэтому 
, последнее влечет справедливость леммы.
Далее займемся оценкой нормы разности 
и 
. Заметим, что при 
,
является реализацией метода Эйлера для уравнения (3) с неточно заданной правой частью.
Отметим, что 
(7)
Теперь, для получения окончательного результата требуется оценить 
и 
.
Введем вспомогательную систему, которую можно трактовать как метод Эйлера, для решения дифференциального уравнения (3) с точно известной правой частью:
(8)
при и 
.
Лемма 5. Пусть выполнены условия леммы 3, тогда существуют 
, 
такие, что всех 
и имеет место неравенство: 
Доказательство. В силу (3) и (8)
.
Из последнего следует оценка сверху для нормы разности 
и 
:
(9)
Рассмотрим 
. Согласно [1] для симметричной матрицы 
имеет место представление 
, где 
- диагональная матрица с элементами 
. Поэтому существует 
такое, что всех 
тогда 
В силу полученной оценки неравенство (9) при 
, 
принимает вид:
из которого, с учетом начальных условий для 
и 
, по индукции получаем
полагая 
, приходим к требуемой оценке.
Рассуждения, аналогичные приведенным в лемме 5, с учетом полученного в ней результата, позволяют сформулировать:
Лемма 6. Пусть выполнены условия леммы 3, тогда существуют 
, 
, 
такие, что всех 
и 
справедливо неравенство: 
,
где 
, 
.
Из лемм 5, 6 непосредственно следует:
Лемма 7. Пусть выполнены условия леммы 3. Тогда для всех
.
Следствие 1. Из ограниченности 
и леммы 7 следует ограниченность 
на 
, при этом существует 
такая, что для всех
имеет место:
Лемма 8. Пусть выполнены условия леммы 3. Тогда существуют 
, 
, 
такие, что всех имеет место неравенство 
.
Доказательство. На основании (7) имеем:
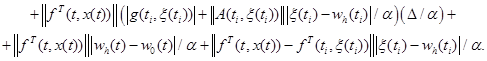
Тогда с учетом следствия 1 из леммы 3, леммы 7, при выборе
,приходим к требуемому результату. Лемма доказана.
На основании лемм 4, 8 справедлива
Теорема (верхняя оценка точности). Пусть выполнены условия леммы 3, 
, тогда верхняя оценка точности в равномерной метрике на имеет вид
Замечание 1. Оптимизация асимптотического порядка верхней оценки точности реализуется выбором 
, , , при этом 
.
Замечание 2. Приближение искомого неизвестного управления из системы (1) будет иметь вид 
.
Рецензенты:
Короткий А.И, д. физ.-мат. н., профессор, зав. отделом ИММ УрОРАН, г. Екатеринбург,
Ким А.В., д. физ.-мат. н., профессор, руководитель группы ИММ УрОРАН, г. Екатеринбург.
Бичурин Мирза Имамович, д.ф.м.н., профессор, заведующий кафедрой проектирования и технологии радиоаппаратуры, Новгородский государственный университет, г. Великий Новгород.