Современная социальная ситуация привела к тому, что в обществе проходит интенсивный процесс изменения социальных ориентиров. Этот процесс получил свое отражение в системе среднего профессионального образования. В настоящее время ССУзы находятся на стадии динамического обновления, при этом в основу образовательного процесса кладется осознание каждым учащимся целей изучения учебного материала, форм и методов своей учебной деятельности, условий успешности процесса обучения; заметно увеличивается степень самостоятельности и ответственности студентов за результаты своего учебного труда.
Современные концепции образования исходят из приоритета цели воспитания и развития личности студента на основе формирования учебной деятельности. Важно создать условия для того, чтобы каждый студент в процессе диагностики своей математической подготовки мог полностью реализовать себя, стал подлинным субъектом учения, желающим и умеющим учиться. Контроль и оценивание знаний должны быть «вариативными к индивидуальным особенностям студентов».
Дифференцированный подход в организации процесса диагностики знаний студентов по математике решает задачи эффективной помощи студенту в совершенствовании его личности и мотивации обучения, занимает промежуточное положение между фронтальной работой со всем коллективом и индивидуальной работой с каждым учащимся [2]. Он облегчает и упорядочивает деятельность педагога, так как позволяет разработать методы диагностики математической подготовки не для каждого обучаемого в отдельности, а для определенной категории студентов.
Необходимость учета индивидуальных особенностей студентов в ходе диагностики их знаний и умений влечет за собой вопрос: как все это осуществить организационно? В современных ССУЗах, где один преподаватель одновременно занимается с большой группой студентов, где накопляемость в группе превышает 30 человек, где собраны студенты с различным уровнем обучаемости, это и является узловой проблемой обучения математике.
Проблема дифференцированного подхода в обучении математике исследуется давно, в педагогике и методике ей всегда уделялось значительное внимание. Однако выдвижение и развитие за последние годы новых концептуальных идей, в частности, идеи планирования обязательных результатов обучения математике, приводит к постепенной перестройке всей методической системы, в том числе позволяет по-новому взглянуть на проблему организации диагностики математической подготовки студентов в условиях дифференцированного обучения.
Предлагаемая ниже концепция организации диагностики математической подготовки студентов в условиях уровневой дифференциации учитывает современные результаты и достижения методической и психологической науки, требующие пересмотра традиционных взглядов, отказа от сложившихся стереотипов.
Термин “уровневая дифференциация” вошёл в методический лексикон недавно, взамен термина “внутренняя дифференциация”, что обусловлено некоторыми особенностями нового подхода. Традиционно дифференцированный подход в обучении, в частности, математике, основывался на психолого-педагогических различиях обучаемых, при этом конечные цели обучения остаются едиными для всех обучаемых, а для многих заведомо непосильными. Сущность дифференциации состояла в поиске приёмов и способов обучения математике, которые индивидуальными путями вели бы всех обучаемых к одинаковому овладению программой. А эта задача не всегда разрешима. Необходимо также отметить отсутствие адекватных механизмов дифференцированного подхода в обучении математике в традиционном его понимании, которые позволяли бы объективно формировать группы обучаемых в зависимости от особенностей их развития и психики. Поэтому оценка индивидуальных возможностей студентов целиком зависит от субъективного мнения преподавателя предметника, что часто ведёт к методическим ошибкам и снижает эффективность дифференцированной работы.
Принципиальное отличие нового подхода состоит в том, что уровневая дифференциация основывается на планировании результатов обучения: явном выделении уровня обязательной математической подготовки и формировании на этой основе повышенных уровней овладения материалом. Сообразуясь с ними и учитывая свои способности, интересы, потребности, студент получает право и возможность выбирать объём и глубину усвоения учебного материала, варьировать свою нагрузку при проверке своих знаний по математике после изучения определенной темы.
Достижение обязательных результатов обучения математике становится при таком подходе тем объективным критерием, на основе которого может видоизменяться ближайшая цель в обучении каждого студента и перестраиваться, в соответствии с этим, содержание его работы. Тогда усилия учащихся направляются на овладение материалом на более высоких уровнях, или продолжается работа по формированию важнейших опорных знаний и умений. Именно такой подход при организации диагностики математической подготовки студентов приводит к тому, что дифференцированная работа получает прочный фундамент, приобретает реальный, осязаемый и для преподавателя, и для студента смысл. Резко увеличиваются возможности работы с сильными студентами, отпадает необходимость постоянно разгружать программы и снижать общий уровень требований, оглядываясь на слабых студентов.
Перечислим ряд важных условий проведения диагностики знаний студентов по математике, выполнение которых необходимо для успешного и эффективного осуществления уровневой дифференциации по дисциплине.
Первое состоит в том, что выделенные уровни усвоения материала и, в первую очередь, обязательные результаты обучения математике должны быть открытыми для студентов. Успех дифференцированного подхода при контроле знаний студентов существенно зависит от их познавательной активности, от того, насколько они будут заинтересованы в своей деятельности. Ясное знание конкретных целей при условии их посильности, возможность выполнять требования преподавателя активизируют познавательные способности студентов, причем на разных условиях. Если цели известны и посильны студенту, а их достижение поощряется преподавателем, то для студента нет ничего естественнее, как стремиться к их выполнению. Поэтому открытость уровневой подготовки является механизмом формирования положительных мотивов учения, сознательного отношения студента к учебной работе.
Второе важнейшее условие – это наличие определённых “ножниц” между уровнем требований и уровнем предлагаемых проверочных заданий. Не следует отождествлять уровень, на котором ведётся преподавание, с обязательным уровнем усвоения материала. Первый должен быть в целом существенно выше, иначе и уровень обязательной математической подготовки не будет достигнут, а студенты, потенциально способные усвоить больше, не будут двигаться дальше.
Иными словами, уровневая дифференциация в ходе диагностики знаний осуществляется не за счет того, что одним студентам предлагают меньшее количество заданий, а другим большее, а в силу того, что, предлагая студентам одинаковый объём материала, мы устанавливаем различные уровни требований к его усвоению.
Третье важнейшее условие, дополняющее предыдущее, состоит в том, что в процессе диагностики математической подготовки студентов должна быть обеспечена последовательность в продвижении студента по уровням. Это означает, что в ходе контроля знаний и умений не следует предъявлять более высоких требований тем студентам, которые не достигли уровня обязательной подготовки. Надо, чтобы трудности в учебной работе были для таких студентов посильными, соответствующими индивидуальному темпу овладения материалом на каждом этапе диагностики их математической подготовки. В то же время, если для одних студентов необходимо продлить этап отработки основных, опорных знаний и умений, то других не следует необоснованно задерживать на этом этапе.
Содержание контроля и оценка должны отражать принятый уровневый подход. Контроль должен предусматривать проверку достижения всеми студентами обязательных результатов обучения математике [1]. Для каждого уровня необходимо разработать соответствующую шкалу оценивания.
И, наконец, четвертое условие, реализация которого в ходе диагностики знаний студентов существенно усиливает эффективность дифференцированного обучения математике, – добровольность в выборе уровня усвоения и отчётности. В соответствии с ним каждый студент имеет право добровольно и сознательно решать для себя, на каком уровне ему усваивать материал. Именно такой подход позволяет формировать у студентов познавательную потребность, навыки самооценки, планирования и регулирования своей деятельности.
Диагностику математической подготовки студентов в условиях уровневой дифференциации можно организовать в разнообразных формах, которые существенно зависят от индивидуальных подходов преподавателя, от особенностей группы студентов, от их возраста и т. д. В качестве основного пути осуществления дифференциации обучения математике предлагается формирование мобильных групп. Деление на уровни (группы) осуществляется, прежде всего, на основе критерия достижения уровня обязательной подготовки. Работа этих групп может проходить в рамках обычных занятий на этапе текущего контроля. Их можно также временно выделить для отдельных занятий на других этапах контроля.
В первом случае целесообразно не ограничиваться дифференцированным подходом в процессе самостоятельной деятельности студентов, а варьировать характер работы групп в зависимости от этапа изучения темы, от потребности в помощи преподавателя.
Во втором случае целесообразно предусмотреть работу и с группами выравнивания, и с группами повышенного уровня.
Организация диагностики математической подготовки студентов в условиях уровневой дифференциации предполагает не только дифференцированную работу в группах, но и подготовку разноуровневых заданий, то есть постоянном дополнении заданий “для всех” индивидуальными заданиями для каждого уровня. Базовый уровень определяется в форме образцов задач, которые студенты должны уметь решать; этот список должен быть открыт, то есть известен студентам [3].
Задания первого уровня предлагаются студентам первой группы, которые имеют пробелы в знаниях программного материала, искажают содержание теорем в применении их к решению задач, самостоятельно могут решить задачи в один-два шага, не умеют вести поиск решения. Эта общая характеристика не исключает различных индивидуальных особенностей учащихся, входящих в первую группу. Здесь могут быть учащиеся, имеющие пробелы в знаниях и отставание в развитии вследствие частых пропусков занятий, в силу плохой систематической подготовки к предмету. Вместе с тем эту группу составляют учащиеся, относящиеся к разным уровням обучаемости. Те из них, кто имеет высокий уровень обучаемости, после ликвидации пробелов в знаниях и при соответствующем обучении обычно быстро переходят на более высокий уровень развития.
Задания второго уровня для студентов второй группы, которые имеют достаточные знания программного материала, могут применять их при решении стандартных задач. Затрудняются при переходе к решению нового типа, но, овладев методами их решения, справляются с решением аналогичных задач. У этих учащихся не сформированы эвристические приемы мышления.
Задания третьего уровня предлагаем для третьей группы студентов, которые могут сводить сложную задачу к цепочке простых подзадач, выдвигать и обосновывать гипотезы в процессе поиска решения задач, переносить прежние знания в новые условия.
Приведем пример разноуровневых заданий, используемых в ходе диагностики знаний студентов по теме «Соотношения между тригонометрическими функциями одного и того же угла».
I уровень
1. Упростите выражение:
![]()
2. Преобразуйте выражение:
![]()
3. Может ли для какого–нибудь угла, выполняться условие:
![]() ,
,![]() ?
?
4. Найдите тригонометрические функции угла, если
![]()
5. Докажите тождество:
![]()
II уровень
1. Упростите выражение:
![]()
2. Преобразуйте выражение:
![]()
3. Могут ли синус и косинус одного и того числа быть равными соответственно:
![]() ?
?
4. Найдите значения других трех основных тригонометрических функций, если
![]()
5. Докажите тождество:
![]()
III уровень
1. Упростите выражение:
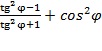
2. Преобразуйте выражение:
![]()
3. Могут ли синус и косинус одного и того числа быть равными соответственно:
![]() ?
?
4. Найдите значения других трех основных тригонометрических функций, если
![]()
5. Докажите тождество:
![]()
Предлагаемая организация диагностики математической подготовки студентов имеет целый ряд преимуществ: даёт преподавателю чёткие ориентиры для отбора содержания дифференцированной работы и позволяет сделать её целенаправленной. Важно, что студент может самостоятельно оценить свои возможности и выбрать для себя тот уровень целей, который соответствует его потребностям в данный момент времени. Ориентация на обязательные результаты обучения постоянно поддерживает подготовку студента на опорном уровне [5]. Это позволяет студенту при возникшем интересе перейти на более высокие уровни на любом этапе обучения. Всё это является гарантией оперативности, гибкости, мобильности дифференциации, создаёт в группе атмосферу взаимного доверия между преподавателем и студентами, способствует активному введению положительных мотивов учения для разных категорий студентов.
Заметим, что достижение уровня обязательной подготовки вовсе не исключает возможности учитывать такие качества студента, как самостоятельность, работоспособность, интерес к обучению, уровень мышления, внимательность и другие качества. Более того, диагностика математической подготовки студентов в условиях уровневой дифференциации позволяет учитывать эти индивидуальные качества в большей степени, не рассматривать их как уже заданные для деления студентов на уровни (группы), а развивать и формировать их у всех студентов в ходе дифференцированной работы.
Итак, основная особенность диагностики математической подготовки студентов ССУЗов в условиях уровневой дифференциации состоит в дифференциации требований к знаниям и умениям студентов: явно выделяется уровень обязательной подготовки, который задаёт достаточную нижнюю границу усвоения материала, он, безусловно, доступен и посилен всем студентам. На его основе формируются повышенные уровни овладения курсом. Студенты получают право и возможность, обучаясь в одной группе и по одной программе, выбирать тот уровень усвоения, который соответствует их потребностям, интересам, способностям.
Разноуровневый контроль, свобода вопросов дают студентам уверенность в знаниях даже сложных тем и разделов дисциплины. Расширяются задачи по определению уровня усвоения для самоконтроля – студент сам определяет, на каком этапе усвоения он находится и сколько баллов (оценку) он получит за правильный ответ. Адекватность самооценки позволяет обеспечить аргументированную оценку знаний студентов, имеющих разную подготовку по дисциплине.
Рецензенты:Найниш Лариса Алексеевна, доктор педагогических наук, профессор, заведующий кафедрой начертательной геометрии и графики, Пензенский государственный университет архитектуры и строительства Министерства образования и науки РФ, г. Пенза.
Мещеряков Анатолий Семенович, доктор педагогических наук, профессор, заведующий кафедрой профессиональной педагогики и психологии, член академии профессионального образования, Пензенский государственный университет Министерства образования и науки РФ, г. Пенза.



