Введение
В процессе цифровой обработки сигналов нередко возникает задача фильтрации сигнала в очень узком частотном диапазоне. Примером такой задачи может служить ситуация, когда сигнал содержит несколько составляющих на близких частотах, и требуется выделить одну из них. Для этого необходимо спроектировать цифровой фильтр с очень узкими относительными полосами пропускания и перехода. В зависимости от расположения составляющих сигнала, это может быть фильтр нижних, верхних частот, полосовой или заграждающий фильтр. Прямое проектирование таких устройств часто приводит к фильтрам очень высоких порядков, практическая реализация которых либо нерациональна, либо невозможна. Использование одного обычного фильтра с конечной импульсной характеристикой (КИХ) для вышеописанных задач нецелесообразно с точки зрения производительности системы и количества выполняемых арифметических операций, необходимых для получения одного отсчёта выходного сигнала. Альтернативный путь решения такой задачи заключается в использовании идей многочастотной дискретизации – последовательном прохождении сигнала через каскады фильтров с изменением частоты дискретизации.
КИХ-фильтр и децимация
КИХ-фильтр, структура которого изображена на рис.1, должен работать в соответствии с уравнением, задающим свертку [3]:
![]() , (1)
, (1)
где h(k) – массив коэффициентов фильтра и x(n-k) – входной массив данных фильтра.
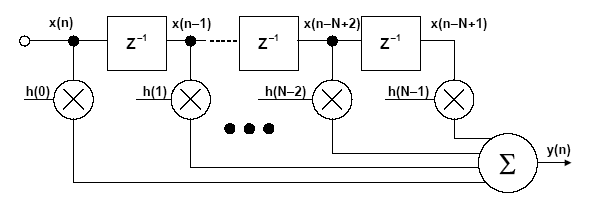
Рис. 1. Фильтр с конечной импульсной характеристикой порядка N
Число N в уравнении представляет собой число звеньев и определяет эффективность фильтра. КИХ-фильтр с числом звеньев N требует N циклов (операций) умножения с накоплением.
Для уменьшения количества выполняемых операций используются 2 подхода: каскадная фильтрация с изменением частоты дискретизации на выходе каждого каскада, когда каждый каскад представляет собой КИХ-фильтр и дециматор, и фильтрация, совмещённая с децимацией.
Децимация, как правило, используется в высокоскоростных системах для понижения частоты дискретизации входного сигнала [4]. Концепция децимации проиллюстрирована на рис.2. Верхняя диаграмма показывает исходный сигнал с полосой fa, который дискретизирован с частотой fs. Диаграмма, содержащая соответствующий спектр, показывает, что частота дискретизации значительно превышает частоту, требуемую для сохранения информации, содержащейся в полосе fa, то есть сигнал с полосой fa является избыточно дискретизированным сигналом. Полоса между частотами fa и fs-fa не содержит никакой полезной информации. Нижняя диаграмма показывает тот же самый сигнал, но частота дискретизации его уменьшена с коэффициентом М.
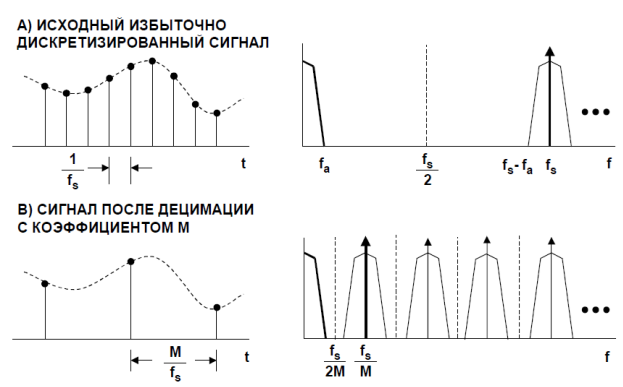
Рис. 2. Децимация дискретного сигнала с коэффициентом M
Реализация каскадной структуры фильтров
Каскадная структура фильтрации представлена на рис. 3.
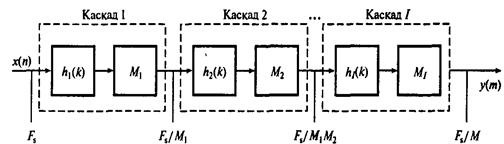
Рис. 3. Процесс многокаскадной децимации
Как уже говорилось выше, в данном случае каждый каскад представляет собой собственно фильтр (hi) и дециматор (Mi). В каскадной структуре частота преобразуется в несколько этапов. В процессе прохода через каскадный фильтр частота дискретизации понижается постепенно, что приводит к существенному понижению требований к фильтрам защиты от наложения спектров и подавления зеркальных частот каждого каскада.
Общий шаг децимации выражается как произведение меньших шагов [1]:
![]() , (2)
, (2)
где целое число Мi – шаг децимации N-го каскада. Каждый каскад – это независимый дециматор, обозначенный пунктирным прямоугольником. Если М»1, многокаскадный подход приводит к значительному снижению требований к вычислениям и памяти, ослаблению характеристик фильтров, используемых в дециматорах, а, следовательно, к использованию фильтров, менее чувствительных к эффектам конечной разрядности.
Названные преимущества возможны за счет увеличения сложности разработки и реализации системы.
Выбор коэффициента децимации и количества каскадов определяется в зависимости от условий конкретной задачи и параметров системы. Однако следует внимательно подходить к выбору коэффициента децимации. При децимации может наблюдаться эффект наложения – элайзинг (рис.4), который заключается в наложении спектров сигналов друг на друга.
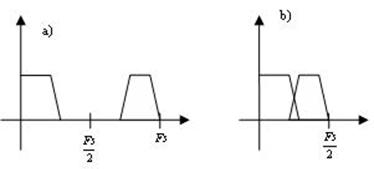
Рис. 4. Иллюстрация эффекта наложения при децимации:
а) дискретный спектр исходного сигнала, b) дискретный спектр сигнала после децимации
Реализуя систему каскадной фильтрации, необходимо получить оптимальное количество каскадов, при котором вычислительные затраты для достижения необходимой частоты дискретизации будут минимизированы. Для расчета необходимого количества каскадов разработан следующий алгоритм.
Например, для выделения узкополосного сигнала в 5 кГц из сигнала с частотой дискретизации 12,5 МГц необходимо провести прореживание в 2500 раз. Сначала определяется исходный коэффициент децимации (для частот 12,5 МГц и 5 кГц он будет равен, соответственно, 2500). Далее этот коэффициент разбивается на простые сомножители. Для этого реализован алгоритм нахождения простых сомножителей по методу Монте-Карло. В самом алгоритме для нахождения наименьшего общего делителя (НОД) использован алгоритм Евклида [2].
После этого достаточно найти такую комбинацию произведений сомножителей, сумма которых будет минимальна. Но так как все сомножители, полученные в результате работы алгоритма, простые, то сумма этих сомножителей и будет искомой.
![]() (3)
(3)
Исключение составляет случай, когда получается два простых сомножителя равных 2. В данном случае 2+2 = 2*2, т.е. с точки зрения сложности структуры каскадного фильтра оптимально использовать один каскад с коэффициентом децимации равным 4, чем два каскада с коэффициентами децимации равными 2.
Так как сумма полученных коэффициентов минимальна, то минимальным окажется и количество циклов умножения с накоплением, используемых в процессе фильтрации. Так, например, для используемого в комплексе коэффициента децимации 2500 получаем следующую комбинацию сомножителей:
![]() (4)
(4)
Однако при этом после каждого каскада децимация сигнала производится с малым коэффициентом децимации. Поэтому на каждый следующий каскад сигнал приходит всё ещё с большой частотой дискретизации, т.е. количество операций умножения с накоплением всё ещё остаётся достаточно большим.
Рассмотрим пример получения 1 отсчёта сигнала с частотой дискретизации 5 кГц из сигнала с частотой дискретизации 12,5 МГц при помощи описанного выше каскадного фильтра. Один отсчёт отфильтрованного сигнала можно получить из 2500 отсчётов исходного. Составим таблицу (табл. 1) количества операций на каждом каскаде.
Табл. 1. Количество операций на каждом каскаде
|
|
Каскад №1 |
Каскад №2 |
Каскад №3 |
Каскад №4 |
Каскад №5 |
|
Коэффициент децимации |
5 |
5 |
5 |
5 |
4 |
|
Размер сигнала на входе (отсчётов) |
2500 |
500 |
100 |
20 |
5 |
|
Длина фильтра |
20 |
20 |
20 |
20 |
16 |
|
Количество операций |
50000 |
10000 |
2000 |
400 |
80 |
Итого, для получения одного отсчёта сигнала понадобится 62480 операций умножения с накоплением (это без учёта операций, необходимых для собственно децимации).
Если использовать только один фильтр с такими же параметрами подавления вне полосы пропускания, нелинейностью АЧХ и т.п., то для получения одного отсчёта нам понадобится 25000000 операций умножения с накоплением. Т.е. без учёта децимации получается выигрыш по количеству операций фильтрации в 400 раз.
Совмещение фильтрации с децимацией
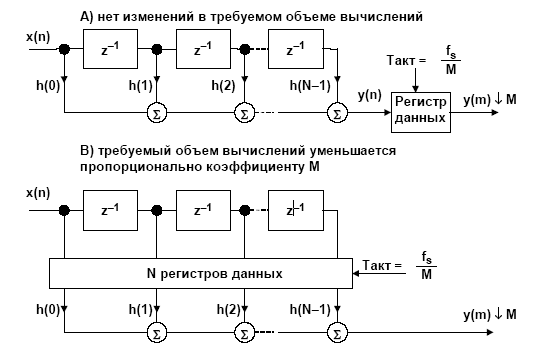
Рис. 5. Децимация, совмещённая с КИХ-фильтрацией
На рис. 5 показана структура системы, выполняющей процедуры фильтрации и децимации последовательно. Данные y(n) с выхода фильтра сохраняются в регистре данных, который стробируется с частотой fs/M, соответствующей частоте дискретизации после децимации. В данном случае децимация не изменяет объема вычислений, требуемых для реализации цифрового фильтра, то есть фильтр должен вычислять каждый выходной отсчет y(n). Как видно из рисунка, не все отсчёты сигнала, рассчитанные в фильтре, используются после процедуры децимации. Многие из них попросту отбрасываются. Следовательно, можно предложить структуру фильтра, в которой «ненужные» отсчёты сигнала не будут рассчитываться, т.е. на их расчет не будет тратиться дополнительное процессорное время.
На рис. 4 В представлен метод, который может использоваться для увеличения с коэффициентом М вычислительной эффективности КИХ-фильтра. Данные из регистров задержки сохраняются в N регистрах данных, которые стробируются частотой, соответствующей частоте дискретизации после децимации fs /M. Операции умножения с накоплением в КИХ-фильтре теперь должны выполняться только в каждом М-ом тактовом цикле. Этот выигрыш в эффективности может быть использован для реализации фильтра с большим количеством звеньев и для проведения дополнительных вычислений. С учётом этого модифицируем таблицу 1 (табл. 2).
Табл. 2. Количество операций на каждом каскаде
|
|
Каскад № 1 |
Каскад № 2 |
Каскад № 3 |
Каскад № 4 |
Каскад № 5 |
|
Коэффициент децимации |
5 |
5 |
5 |
5 |
4 |
|
Размер сигнала на входе (отсчётов) |
2500 |
500 |
100 |
20 |
5 |
|
Длина фильтра |
20 |
20 |
20 |
20 |
16 |
|
Количество операций |
10000 |
2000 |
400 |
80 |
20 |
Общее количество операций по получению 1 отсчёта сигнала получается равным 12500.
Если использовать один децимирующий КИХ-фильтр, то количество операций будет равно 25000000/2500 = 10000. Таким образом, при использовании децимирующих КИХ-фильтров использование каскадной фильтрации по критерию количества математических операций за единицу времени не целесообразно. Однако метод каскадной фильтрации позволяет экономить такой немаловажный ресурс, как память при реализации цифровой фильтрации на цифровых процессорах обработки сигналов [5], а для реализации в ПЛИС – количество используемых аппаратных умножителей и логических ячеек.
Из выше сказанного следует, что при выделении узкополосного сигнала в ПЭВМ целесообразней использовать один децимирующий КИХ-фильтр, а при реализации цифрового фильтра в ПЛИС с ограниченным числом логических ячеек или на сигнальном процессоре, память которого ограничена по объёму, лучше всего применять каскадную фильтрацию.
Работа выполнена при финансовой поддержке МИНОБРНАУКИ России и Российского фонда фундаментальных исследований.
Рецензенты:
Водяхо А. И., доктор технических наук, профессор, профессор кафедры ВТ ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Дмитревич Г. Д., доктор технических наук, профессор, профессор кафедры САПР ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.



