Введение
Одной из основных целей нейтронно-физических расчетов ядерных реакторов является оценка различных функционалов плотности потока нейтронов, описывающих стационарное состояние и временное поведение реактора. Однако многие параметры, характеризующие динамику поведения нейтронного поля в ядерном реакторе, являются дробно-билинейными функционалами плотности потока и ценности нейтронов (например, время жизни мгновенных нейтронов, эффективная доля запаздывающих нейтронов, коэффициенты реактивности). Данная статья посвящена изучению возможности применить теорию малых возмущений для оценки чувствительности дробно-билинейных функционалов к возмущениям изотопного состава реактора. Время жизни мгновенных нейтронов рассмотрено как пример такого функционала.
Формулы теории малых возмущений для дробно-билинейных функционалов
Уравнение для распределения плотности потока в реакторе ![]() можно записать в следующей операторной форме:
можно записать в следующей операторной форме:
![]() (1)
(1)
где ![]() оператор многогруппового диффузионного приближения, описывающий перенос, поглощение и замедление нейтронов,
оператор многогруппового диффузионного приближения, описывающий перенос, поглощение и замедление нейтронов, ![]() оператор, описывающий генерацию нейтронов деления, а
оператор, описывающий генерацию нейтронов деления, а ![]() эффективный коэффициент размножения нейтронов.
эффективный коэффициент размножения нейтронов.
Время жизни мгновенных нейтронов можно вычислить как функционал [2]:
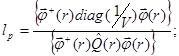 (2)
(2)
где ![]() векторные функции групповых плотностей потока и ценности нейтронов, соответственно;
векторные функции групповых плотностей потока и ценности нейтронов, соответственно;
![]() диагональная матрица обратных скоростей нейтронов; а фигурные скобки здесь и далее обозначают интегрирование по всей области определения пространственных и энергетических переменных. Если обозначить
диагональная матрица обратных скоростей нейтронов; а фигурные скобки здесь и далее обозначают интегрирование по всей области определения пространственных и энергетических переменных. Если обозначить ![]() концентрацию изотопа
концентрацию изотопа ![]() в зоне
в зоне ![]() , то коэффициент чувствительности реактивности к изменению изотопного состава можно вычислить как следующий дробно-билинейный функционал:
, то коэффициент чувствительности реактивности к изменению изотопного состава можно вычислить как следующий дробно-билинейный функционал:
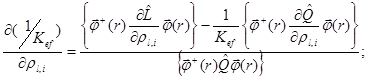
Уравнение, описывающее пространственно-энергетическое распределение ценности нейтронов, аналогично уравнению (1) и отличается от него лишь использованием сопряженных по Лагранжу операторов, т.е. ![]()
В общем виде дробно-билинейные функционалы плотности потока и ценности нейтронов можно записать так:
![]() (3)
(3)
где ![]() матрицы, называемые ядрами функционалов. Например, для времени жизни мгновенных нейтронов:
матрицы, называемые ядрами функционалов. Например, для времени жизни мгновенных нейтронов: ![]() а для коэффициента чувствительности реактивности:
а для коэффициента чувствительности реактивности: 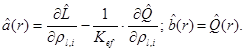
При слабых изменениях концентраций изотопов вариации дробно-билинейных функционалов можно оценивать по формулам теории малых возмущений [5]. Общий формализм теории возмущений предполагает построение расширенного функционала (лагранжиана), в котором к искомому функционалу с помощью множителей Лагранжа присоединяются уравнения, описывающие распределения функций. Затем из условия стационарности лагранжиана находятся уравнения для множителей Лагранжа и выводятся формулы теории возмущений.
В рассматриваемом случае лагранжиан имеет вид:
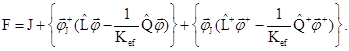 (4)
(4)
тогда
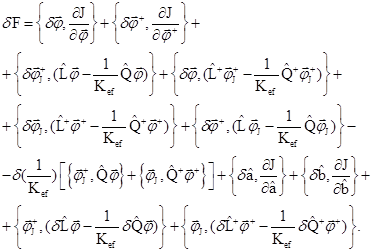
Перегруппируем члены этого выражения:
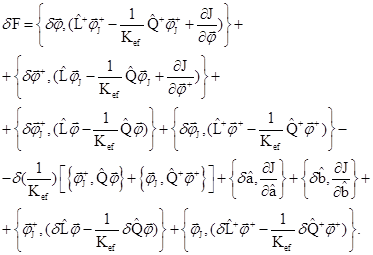 (5)
(5)
Функциональные производные по плотности потока и ценности нейтронов можно найти из следующих соотношений:
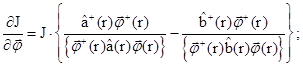
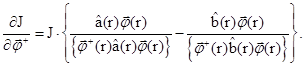 (6)
(6)
Члены с вариациями ядер искомого функционала можно записать так:
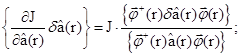
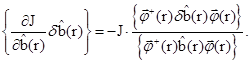
Для того чтобы исключить влияние вариации плотности потока нейтронов ![]() на вариацию лагранжиана, неоднородное сопряженное уравнение для множителя Лагранжа
на вариацию лагранжиана, неоднородное сопряженное уравнение для множителя Лагранжа ![]() запишем так:
запишем так:
![]() (7)
(7)
Аналогично, для того чтобы исключить влияние вариации ценности нейтронов ![]() на вариацию лагранжиана, неоднородное прямое уравнение для множителя Лагранжа
на вариацию лагранжиана, неоднородное прямое уравнение для множителя Лагранжа ![]() запишем так:
запишем так:
![]() (8)
(8)
Функциональные производные ![]() и
и ![]() , являющиеся членами неоднородных уравнений (7), (8), ортогональны к решениям соответствующих однородных уравнений. Это легко показать, используя вид этих производных (6), т.е.
, являющиеся членами неоднородных уравнений (7), (8), ортогональны к решениям соответствующих однородных уравнений. Это легко показать, используя вид этих производных (6), т.е. ![]()
![]()
Согласно альтернативе Фредгольма, из этого следует существование решений неоднородных уравнений (7) и (8). Из условия слабой чувствительности лагранжиана к погрешностям при вычислении множителей Лагранжа ![]() и
и ![]() могут быть получены однородные уравнения для плотности потока и ценности нейтронов:
могут быть получены однородные уравнения для плотности потока и ценности нейтронов:
![]()
![]() (9)
(9)
Очевидно, что системы (9) и (7, 8) должны решаться последовательно, поскольку только найдя решения системы (9), т.е. функции плотности потока ![]() и ценности нейтронов
и ценности нейтронов ![]() , можно определить функциональные производные, входящие в правую часть неоднородных уравнений системы (7, 8).
, можно определить функциональные производные, входящие в правую часть неоднородных уравнений системы (7, 8).
Известно, что общее решение неоднородного уравнения равно общему решению соответствующего однородного уравнения плюс любое частное решение самого неоднородного уравнения. Для того чтобы найти частное решение неоднородного уравнения из его общего решения, необходимо вычесть общее решение соответствующего однородного уравнения, т.е.:
![]()
![]() (10)
(10)
Будем искать такие частные решения уравнений (7, 8), которые были бы ортогональны источникам нейтронов деления в однородных уравнениях, т.е.:
![]()
![]() (11)
(11)
Константы ортогонализации можно вычислить следующим образом:

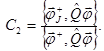
Выбор такого частного решения позволит избавиться от члена, учитывающего вариацию ![]() в выражении для вариации лагранжиана, поскольку
в выражении для вариации лагранжиана, поскольку ![]() в соответствии с условиями (11).
в соответствии с условиями (11).
В результате проведенных преобразований получаем, что вариация лагранжиана, вызванная, например, вариацией концентрации изотопа ![]() в зоне
в зоне ![]() , будет равна:
, будет равна:
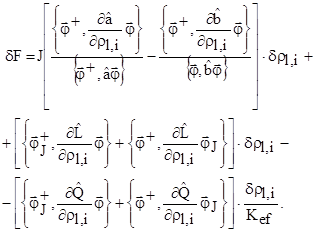 (12)
(12)
Первый член в правой части выражения (12) учитывает явную зависимость ядер искомого функционала от изотопного состава реактора, второй член учитывает влияние изменений изотопного состава на процессы переноса, поглощения и замедления нейтронов, а последний член – на процесс генерации нейтронов деления. Из теории функционального анализа [3] известно, что в точке стационарности ![]() тождественен искомому функционалу
тождественен искомому функционалу ![]() , вариация первого порядка лагранжиана
, вариация первого порядка лагранжиана![]() равна вариации первого порядка функционала
равна вариации первого порядка функционала ![]() , а погрешность в определении функционала
, а погрешность в определении функционала ![]() обладает вторым порядком малости по отношению к погрешностям в определении функций
обладает вторым порядком малости по отношению к погрешностям в определении функций ![]() и
и ![]()
Таким образом, выражение (12), связывающее возмущения ядер функционала и операторов уравнения переноса с возмущением лагранжиана, и есть формула теории малых возмущений для искомого дробно-билинейного функционала.
Использование формул теории малых возмущений
Применение формулы теории малых возмущений (12) для оценки изменения дробно-билинейного функционала можно продемонстрировать на следующем примере. Пусть искомый дробно-билинейный функционал имеет вид:
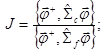
где ![]() диагональная матрица групповых макросечений радиационного захвата нейтронов, а
диагональная матрица групповых макросечений радиационного захвата нейтронов, а![]() диагональная матрица групповых макросечений деления.
диагональная матрица групповых макросечений деления.
Тогда чувствительность дробно-билинейного функционала к изменению концентрации изотопа ![]() в зоне
в зоне ![]() можно определить следующим образом.
можно определить следующим образом.
Первый член выражения (12), учитывающий явную зависимость ядер функционала от изотопного состава реактора, будет равен:
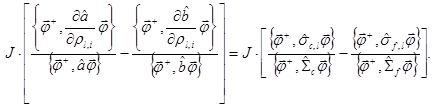
Второй член выражения (12) описывает вклад процессов переноса, поглощения и замедления нейтронов, а третий член выражения (12) описывает вклад процесса генерации нейтронов деления в чувствительность дробно-билинейного функционала к изменению изотопного состава реактора.
Изложенная выше методика расчета коэффициентов чувствительности дробно-билинейных функционалов была использована для расширения вычислительных возможностей программы TIME26 [1]. Тестовые расчеты проводились для одномерной сферической модели быстрого реактора БРЕСТ-ОД-300 [4] со свинцовым теплоносителем. Геометрическая модель включала три активные зоны с одинаковым содержанием плутониевой фракции в смешанном уран-плутониевом нитридном топливе, но с разными (малым, средним и большим) диаметрами твэлов, и свинцовый боковой экран. В качестве дробно-билинейного функционала выбрано время жизни мгновенных нейтронов:
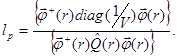
Характерной особенностью этого функционала является независимость его ядер от концентраций неделящихся изотопов. Поэтому вклад в изменение времени жизни мгновенных нейтронов дают не ядра функционала, а только члены выражения (12), описывающие процессы утечки, поглощения и замедления нейтронов. Если же изменяется содержание делящихся изотопов, то в оценке возмущения![]() участвуют все члены формулы теории малых возмущений. Формула (12) хороша еще и тем, что позволяет выявить вклад нейтронных процессов (радиальная и аксиальная утечка, поглощение нейтронов в
участвуют все члены формулы теории малых возмущений. Формула (12) хороша еще и тем, что позволяет выявить вклад нейтронных процессов (радиальная и аксиальная утечка, поглощение нейтронов в ![]() - и
- и ![]() -реакциях, замедление нейтронов при упругом и неупругом рассеянии, размножение нейтронов) в изменение функционала.
-реакциях, замедление нейтронов при упругом и неупругом рассеянии, размножение нейтронов) в изменение функционала.
Расчетные блоки, предназначенные для оценки возмущений дробно-билинейных функционалов, верифицировались следующим образом. С помощью формулы теории малых возмущений и прямых расчетов оценивалось возмущение времени жизни мгновенных нейтронов, вызванное уменьшением на 10% содержания 239Pu и свинца в разных зонах реактора, т.е. зонах малого, среднего и большого диаметра твэлов (ЗМД, ЗСД, ЗБД) и в боковом экране (БЭК). Результаты прямых расчетов и расчетов по формуле теории малых возмущений приведены в табл. 1. Видно их хорошее согласование. В таблице использованы следующие обозначения:
![]() – возмущенное значение
– возмущенное значение ![]() , связанное только с явной зависимостью его ядер от изотопного состава;
, связанное только с явной зависимостью его ядер от изотопного состава;
![]() – возмущенное значение
– возмущенное значение ![]() , рассчитанное по теории малых возмущений;
, рассчитанное по теории малых возмущений;
![]() – возмущенное значение функционала, полученное прямым расчетом.
– возмущенное значение функционала, полученное прямым расчетом.
Таблица 1 – Изменение времени жизни мгновенных нейтронов ![]() (10-7 сек) при уменьшении на 10% концентрации 239Pu и свинца. Невозмущенное значение
(10-7 сек) при уменьшении на 10% концентрации 239Pu и свинца. Невозмущенное значение ![]() = 4.720•10-7 сек.
= 4.720•10-7 сек.
|
Параметр/Зона |
ЗМД |
ЗСД |
ЗБД |
БЭК |
|
Изменяется концентрация 239Pu |
||||
|
|
4.876 |
4.827 |
4.760 |
- |
|
|
4.999 |
4.825 |
4.712 |
- |
|
|
5.001 |
4.812 |
4.714 |
- |
|
|
0.045 |
0.270 |
0.036 |
- |
|
|
Изменяется концентрация свинца |
|||
|
|
4.667 |
4.719 |
4.718 |
4.493 |
|
|
4.666 |
4.718 |
4.728 |
4.518 |
|
|
0.011 |
0.007 |
0.202 |
0.573 |
Выводы
Успешная апробация изложенных в предыдущем разделе итерационных алгоритмов проведена на простейших одномерных моделях. Однако общий характер предложенных методик вселяет уверенность, что и в случае их реализации на многомерных моделях результат будет положителен.
Рецензенты:
Загребаев Андрей Маркоянович, д.ф.-м.н., профессор ФГАОУ ВПО «Национальный исследовательский ядерный университет «МИФИ», г. Москва.
Точеный Лев Васильевич, д.т.н., ст. научный сотрудник МНТЦ, профессор МГТУ им. Н.Э. Баумана, г. Москва.




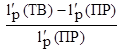 ,%
,%