В последнее время увеличилось количество нештатных ситуаций, происходящих из-за поломок техники, а также возникающих при её нестандартном поведении. Обычно причинами таких явлений становятся ошибки проектирования или износ. Таким образом, наряду с улучшением качества проектирования важной задачей является оценка и анализ процессов систем в реальном времени с целью поддержания ее работоспособности и прогнозирования возможных отказов.
Одной из используемых характеристик системы, оценивающих возможность будущего отказа системы, является первый показатель Ляпунова [5]. Данный показатель, за исключением некоторых случаев [1], является индикатором стремления системы к равновесию. Наличие в спектре характеристических показателей системы хотя бы одного положительного ляпуновского показателя означает неустойчивость фазовой траектории. Следовательно, одной из основных задач при оценке устойчивости является нахождение наибольшего ляпуновского показателя.
В статье приводятся и сопоставляются данные о проведенных исследованиях по существующим методам расчета первого показателя, а также по специальным методам, разработанным авторами данной статьи. В ходе исследования рассматривались такие существующие методы, как метод Вольфа [4], метод Розенштейна [3], МНК, в приложении к оценке первого показателя. Были разработаны интерполяционный метод, логарифмический метод и метод выделения логарифма, причем последний полностью реализован блоками пакета Matlab/Simulink. Была также разработана модификация сингулярного разложения (SVD), позволяющая оценивать значение первого показателя.
Каждый из рассмотренных методов дает возможность проанализировать произвольный временной ряд, характеризующий переходный процесс в системе. В результате анализа возможно определение значение первого показателя Ляпунова, который практически полностью характеризует переходный процесс в системе. Резкие изменения этого показателя сигнализируют о потенциальных проблемах или неполадках.
Далее приведено краткое описание трех разработанных методов: логарифмического, интерполяционного и метода выделения логарифма. Рассмотрена схема тестирования методов и представлены его результаты.
Первый метод (Логарифмический)
В методе исследуется временной ряд, представляющий собой численное решение некоторого дифференциального уравнения с постоянным шагом времени Δt и одним состоянием равновесия типа - фокус: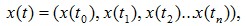 где
где 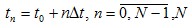 - количество точек решения. Элементы ряда преобразуются следующим образом:
- количество точек решения. Элементы ряда преобразуются следующим образом:
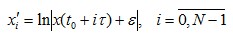
где 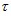 - шаг дискретизации. Модуль под знаком логарифма исключает влияние знака функции на значение логарифма. Относительное рассогласование с состоянием равновесия остается таким же, хотя и меняется знак производной. Введение малой величины исключает бесконечность логарифма в точках x(t) = 0. Для нового получившегося ряда производится реконструкция и составляется матрица χ вида:
- шаг дискретизации. Модуль под знаком логарифма исключает влияние знака функции на значение логарифма. Относительное рассогласование с состоянием равновесия остается таким же, хотя и меняется знак производной. Введение малой величины исключает бесконечность логарифма в точках x(t) = 0. Для нового получившегося ряда производится реконструкция и составляется матрица χ вида:

Из матрицы X рассчитывается среднее суммарное отображение s по всем сдвинутым относительно друг друга во времени реконструированным рядам 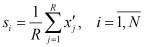 . После дополнительной фильтрации s можно посчитать первый показатель по следующей формуле:
. После дополнительной фильтрации s можно посчитать первый показатель по следующей формуле:
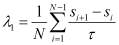
Второй метод (Интерполяционный)
Пусть решение дифференциального уравнения может приближенно представляться в виде 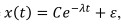 , где ε - состояние равновесия, λ - первый показатель Ляпунова, С - константа. Производная от такого решения будет выглядеть как
, где ε - состояние равновесия, λ - первый показатель Ляпунова, С - константа. Производная от такого решения будет выглядеть как 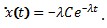 . Соответственно, если ε=0, можно найти показатель в виде:
. Соответственно, если ε=0, можно найти показатель в виде:
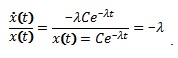
Для такого случая показатель является усредненным отношением точек производной временного ряда к точкам самого ряда. Но нулевое состояние равновесия без отклонений бывает редко. Поэтому, если ошибка не равна 0, необходимо действовать следующим образом.
Рассмотрим числовой ряд, представляющий собой численное решение некоторого дифференциального уравнения с постоянным шагом времени Δt:
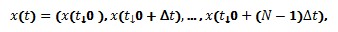
Где N - количество точек решения. Обозначим 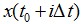 , как xi. Представим, что шаг временного ряда равен kΔt, где k - натуральное число. Таким образом, получаем формулу для расчета первого показателя:
, как xi. Представим, что шаг временного ряда равен kΔt, где k - натуральное число. Таким образом, получаем формулу для расчета первого показателя:
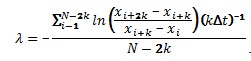
Третий метод (метод выделения логарифма)
Метод состоит из модификаций временного ряда, помогающих исключить параметры, которые сильно затрудняют расчет. Рассматривается преобразование, исключающее точки равновесия и константы при расчете показателя.
Для временного ряда решение уравнения представляется в виде 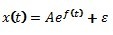 , где A,ε - константы. Константа ε при f(t) <0, t→∞ является точкой равновесия.
, где A,ε - константы. Константа ε при f(t) <0, t→∞ является точкой равновесия.
Предположим, что существует такая же функция, но с запаздыванием по времени 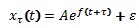 , где
, где 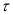 - шаг запаздывания. При вычитании x(t) и x2 (t) избавляемся от ε:
- шаг запаздывания. При вычитании x(t) и x2 (t) избавляемся от ε:
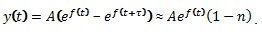
Если считать А и (1-n) константами, то функцию y(t) можно представить в виде 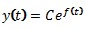 , где склонность системы к неустойчивости определяется не самой функцией f(t), а ее производной. Производную можно посчитать следующими двумя путями.
, где склонность системы к неустойчивости определяется не самой функцией f(t), а ее производной. Производную можно посчитать следующими двумя путями.
1. Для функции y(t) находится ее производная по времени. Далее производная делится на саму функцию y(t).
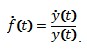
2. От модуля y(t) функции берется логарифм и от 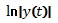 берется производная по времени:
берется производная по времени:
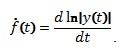
Таким образом, мы избавляемся от постоянной C.
При расчете показателя довольно большое влияние на точность расчета оказывает периодическая составляющая процесса. Предлагается следующий алгоритм ее подавления. Для временного ряда решение уравнения представляется в виде 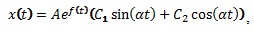 , где A, C1, C2 константы, α - частота колебаний. Можно представить x(t) в виде
, где A, C1, C2 константы, α - частота колебаний. Можно представить x(t) в виде 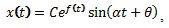 , где
, где 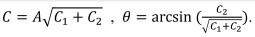 Предполагая, что период колебаний синуса намного меньше по времени, чем экспоненциальное затухание, можно представить сдвинутый во времени ряд таким образом:
Предполагая, что период колебаний синуса намного меньше по времени, чем экспоненциальное затухание, можно представить сдвинутый во времени ряд таким образом:
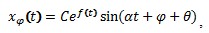 ,
,
где φ - фазовый сдвиг ряда с запаздыванием. Выбирая φ таким образом, чтобы оно равнялось 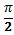 , получаем
, получаем 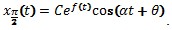 . Отсюда:
. Отсюда:
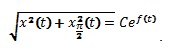 .
.
Применим все эти преобразования к исходному временному ряду, обратим состояние равновесия в ноль, а затем исключим колебания. Далее приводим ряд к виду экспоненциального затухания. После этого, используя преобразование выделения логарифма, находим значения производной функции f(t) в показателе наибольшей экспоненты, принадлежащей решению нестационарного уравнения. Эта производная является признаком локальной во времени устойчивости.
В пакете Matlab/Simulink был реализован блок, воспроизводящий все этапы этого алгоритма; структурная схема показана на рисунке.
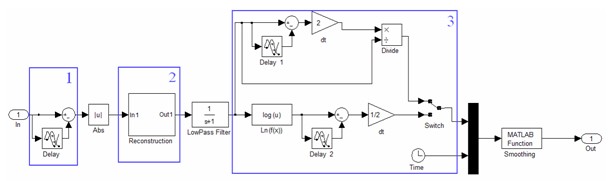
Рисунок. Структурная схема блока, реализующего алгоритм оценки первого показателя
Здесь выделенный элемент 1 соответствует процедуре исключения из расчета состояния равновесия. Элемент 2 соответствует процедуре исключения колебаний и выделения тренда путем преобразования реконструированных рядов. Элемент 3 соответствует реализации двух вышеобозначенных алгоритмов выделения функции 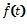 . Также блок снабжен фильтром высоких частот для дополнительного сглаживания тренда и блоком Smoothing, который осуществляет фильтрацию полученных результатов.
. Также блок снабжен фильтром высоких частот для дополнительного сглаживания тренда и блоком Smoothing, который осуществляет фильтрацию полученных результатов.
Исходные данные тестирования методов
Сравнивались результаты использования разработанных методов при оценке первого показателя для трех тестовых систем, обладающих различными динамическими свойствами.
- Модель следящей системы 3-го порядка с контуром по положению в качестве линейной стационарной системы. И та же модель с известной функцией изменения показателя (нестационарная).
- Для описания нелинейной стационарной системы используется осциллятор Ван-дер-Поля со встроенным экспоненциальным затуханием [6]. Для моделирования нестационарного случая к выходной переменной добавляется экспоненциальный множитель.
- В качестве сложной стационарной системы используется модель управления линейным электродвигателем (ЛЭД) типа DDV с обратной связью по усилию [2]. В нестационарном случае производится имитация постепенного отказа обратной связи по усилию.
В качестве наиболее значимых критериев эффективности методов использовались точность и скорость расчета показателя для одиночного ряда.
Точность расчета показателя для временного ряда размерности N определялась как оценка среднего значения отклонения от теоретического значения на заданном промежутке времени 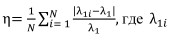 - оценка показателя на промежутке времени
- оценка показателя на промежутке времени 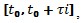 , (
, (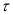 - шаг временного ряда), λ1 - теоретическое значение показателя.
- шаг временного ряда), λ1 - теоретическое значение показателя.
В нестационарном случае берутся крайние значения показателя на выделенном промежутке времени 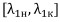 ] и сравниваются с теоретическими.
] и сравниваются с теоретическими.
Средняя скорость расчета показателя за временной промежуток tср оценивается таким образом: 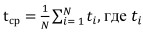 - время расчета первого показателя на i-ом шаге.
- время расчета первого показателя на i-ом шаге.
Расчеты производились на компьютере с процессором Intel(R) Core(ТМ) DuoCPUE7200 @ 2.53 GHz. RAM - 4GB. Использовалась среда Matlab. Непосредственный расчет некоторых методов осуществлялся в разработанных Net библиотеках, для ускорения расчетов.
Результаты тестирования методов
Результаты оценки точности методов представлены в таблице 1. В таблице для каждой модели и метода записаны 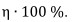 .
.
Таблица 1
|
Модели |
Стационарная |
Нестационарная |
||
|
Методы |
Линейная |
Нелинейная |
Линейная |
Нелинейная |
|
Вольф |
5-10% |
6-12% |
20-30% |
---- |
|
Розенштейн |
2-3% |
1-1.5% |
4-7% |
2-7% |
|
SSA |
1-3% |
2-4% |
3-5% |
3-8% |
|
МНК |
0.5-1% |
--- |
2-6% |
--- |
|
Логарифмический |
1-2% |
1-2% |
3-7% |
2-7% |
|
Интерполяционный |
0.5-2% |
0.5-1.6% |
2-5% |
2-8% |
|
Выделение логарифма |
0.2-1% |
0.2-1% |
3-8% |
3-10% |
Результаты оценки скорости методов для одинаковых размеров рядов (150 точек) представлены в таблице 2. Скорость дана в миллисекундах/расчет.
Таблица 2
|
Модели |
Стационарная |
Нестационарная |
||
|
Методы |
Линейная |
Нелинейная |
Линейная |
Нелинейная |
|
Вольф |
1.8 |
3 |
0.8 |
--- |
|
Розенштейн, C# |
0.2 |
0.17 |
0.2 |
0.18 |
|
SSA |
20 |
10 |
17 |
17 |
|
МНК |
129 |
--- |
126 |
--- |
|
Логарифмический |
1 |
1 |
1 |
1.4 |
|
Интерполяционный, C# |
0.5 |
0.5 |
0.44 |
0.37 |
В табл. 2 выделены методы, обеспечившие наибольшую точность в оценке первого показателя. Прочерками показаны методы, которые были неспособны дать адекватную оценку показателя.
По скорости работы (по убыванию) методы можно расположить таким образом.
- Методы простой обработки ряда, реализованные на C#, скорость - десятые доли миллисекунд.
- Методы простой обработки ряда, реализованные на Matlab, скорость - миллисекунды.
- Методы, содержащие расчет больших матриц (SSA), скорость - десятки миллисекунд.
- Методы, содержащие итерационный поиск минимума функции (МНК), скорость - сотни миллисекунд.
Для метода выделения логарифма невозможно было составить процедуру оценки средней скорости расчета показателя, так как метод создан для реализации в Simulink и не поддерживает функцию оценки скорости одиночного расчета.
Выводы
В ходе работы были рассмотрены как уже существующие методы оценки первого показателя Ляпунова, так и те, которые были разработаны авторами за последние несколько лет.
Было показано, что наилучшими характеристиками точности оценки первого показателя для стационарных систем обладают метод Розенштейна и разработанные авторами статьи интерполяционный метод и метод выделения логарифмов. При их использовании для одинаковых временных рядов (150 точек) отклонение от теоретического значения показателя тестовой модели не превышает 2 %.
Для линейных нестационарных наилучшие результаты демонстрирует интерполяционный метод, а для нестационарных и нелинейных систем - метод Розенштейна и логарифмический. Отклонение от теоретического значения в условиях изменяющегося значения показателя не превышает 7 %.
Наилучшие результаты по скорости по сравнению с другими методами дала реализация на платформе .Net расчета показателя по методу Розенштейна. Скорость расчета показателя для размерности ряда 150 точек составляет от 0.17 до 0.2 мс/расчет.
Рецензенты:
Путов Виктор Владимирович, доктор технических наук, профессор, СПбГЭТУ, г. Санкт-Петербург.
Микеров Александр Геннадьевич, доктор технических наук, профессор, СПбГЭТУ, г. Санкт-Петербург.



