В настоящее время существует большое количество экспериментальных данных по исследованию акустоэлектрических преобразований в гетерогенных диэлектрических и слабопроводящих материалах под действием импульсного механического возбуждения [1-4]. Суть явления акустоэлектрических преобразований состоит в смещении зарядов двойных электрических слоев на границе раздела фаз в гетерогенных материалах и деформации пьезоэлектрических включений акустическими волнами, созданными импульсным механическим возбуждением. Показано, что основной вклад в генерирование электрического отклика на импульсное механическое возбуждение вносят пьезоэлектрические источники акустоэлектрических преобразований [2-3].На основе этих исследований ведется разработка неразрушающих методов контроля структурных и механических характеристик гетерогенных материалов [5-8].
Для повышения точности разрабатываемых методов в рамках данной работы проведены экспериментальные и теоретические исследования акустоэлектрических преобразований при ударном возбуждении гетерогенных материалов, содержащих пьезоэлектрические включения. Типичными представителями таких материалов являются бетоны и горные породы, содержащие включения природного кварца.
Экспериментальные исследования были выполнены с помощью лабораторного комплекса, позволяющего производить импульсное механическое возбуждение образцов и регистрацию электрического отклика. Механическое возбуждение производили с помощью электромеханического ударного устройства с нормированной силой удара, порядка 300 Н. Удар производился по металлической пластине, помещенной на поверхность образца в месте удара. Для регистрации электрического сигнала использовался дифференциальный электрический датчик, позволяющий существенно повысить соотношение сигнал-помеха. Измерительный приемник располагался на расстоянии 2 мм от поверхности образца, а компенсационный - параллельно измерительному на высоте 30 мм от него. Сигнал с электрического датчика регистрировался с помощью платы ввода-вывода «NIPCI-6251», позволяющей осуществлять оцифровку временной реализации электрического сигнала.
Проведенных экспериментальных исследований недостаточно для понимания закономерностей акустоэлектрических преобразований в образцах с определенной геометрией расположения относительно выбранной системы координат точки удара, источников акустоэлектрических преобразований, приемника электрического сигнала.
Для решения этих вопросов были проведены экспериментальные и теоретические исследования параметров электрического отклика на ударное возбуждение модели, содержащей единичный источник акустоэлектрических преобразований. В качестве источника был использован пьезоэлектрический элемент из ЦТС-керамики диаметром 5 мм и толщиной 2 мм. Модель представляла собой образец гипса размером 100х100х100 мм, в геометрический центр которой был помещен пьезоэлектрический элемент.
Тогда, мы имеем конфигурацию системы удара, источника внутри образца и заданной точки приемника такую, как показано на рисунке 1 (в двумерном приближении).
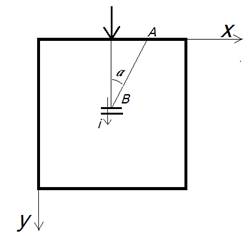
Рисунок 1. Схематическое расположение пьезоэлектрического источника в образце относительно заданного элемента электрического приемника
На рисунке символом I обозначен единичный вектор направления дипольного момента Рпьезоэлемента, расположенного в точке B, численное значение которого является произведением величины заряда q на одной из поверхности на расстояние между поверхностями l (толщина пьезоэлемента). r - радиус-вектор от источника к заданной точке A поверхности приемного датчика. Толстой стрелкой обозначено направление удара по образцу. Образец находится в системе координат x-y, α - угол между направлениемдипольного момента ирадиус-вектором r.
Электрический сигнал из гетерогенных диэлектрических материалов представляет собой ток смещения, возникающий при деформации и смещении источников акустоэлектрических преобразований акустической волной [3, 8], формирующейся в образцах конечных размеров при ударном возбуждении. Ток смещения в диэлектриках определяется потоком вектора электрической индукции через некоторую поверхность:
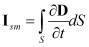
В общем виде вектор электрической индукции диполя, расположенного на расстоянии r от рассматриваемой точки поля,
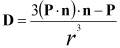 ,
,
где n - единичный вектор в направлении r.
При расположении приемной пластины электрического датчика параллельно оси x ток смещения будет определяться вертикальной составляющей вектора индукции (Dy).
Вертикальная составляющая вектора электрической индукции в точке А при расположении пьезоэлектрического элемента параллельно приемнику (направление диполя совпадает с осью y) имеет вид:
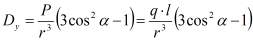 (1)
(1)
Заряд (q), возникающий при деформации пьезоэлектрического элемента, определяется через пьезоэлектрический модуль (d) и силу (F) как q=d·F. l - толщина пьезоэлектрического элемента.
Временная зависимость q(t) определяется силой, с которой акустическая волна при своем движении воздействует на источник в виде пьезоэлектрического элемента. Временные зависимости l(t) и r(t) обусловлены деформациями пьезоэлектрического элемента и материала образца в зоне источник - приемник под действием той же силы F, действующей в объеме образца в соответствии с законом Гука:
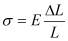 ,
,
где Ϭ=F/S; F - сила, действующая на площадку S; E- модуль Юнга; ∆L - абсолютное перемещение на интервале длины L.
Так как ток смещения, протекающий через поверхность приемника, определяется скоростью изменения электрической индукции, определим элемент этого тока, продифференцировав по времени уравнение (1):
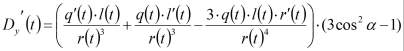
где
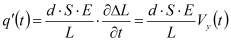 ,
,
Где: S - площадь поперечного сечения образца гипса; E - модуль Юнга гипса; L - размер модели из гипса в направлении возбуждения; Vy (t ) - скорость смещения в гипсе вдоль оси y.
При деформации источника, пьезоэлектрическая ось которого направлена по оси y,
ly(t)=l+∆ly(t); r(t)=r+∆r(t):
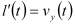
vy(t) - скорость смещения в пьезоэлементе,
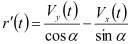
Vх(t) - скорость смещения в гипсе вдоль оси x.
Тогда:
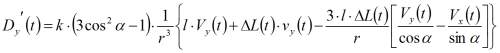 (2)
(2)
Где: 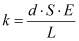
Вторым и третьим слагаемыми в фигурных скобках выражения (2) можно пренебречь, по крайней мере, для случая, когда расстояние между зарядами в диполе (в данном случая l - это толщина пьезоэлектрического элемента, равная 2 мм) намного больше величины смещения, вызванного упругой волной, сформировавшейся в образце в результате удара.
Тогда полный ток смещения от единичного пьезоэлектрического источника:
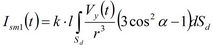 ,
,
где Sd - площадь измерительного электрического приемника.
Аналогичным образом был проведен расчет для случая, когда пьезоэлектрическая ось источника направлена по оси y:
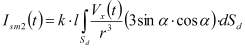
Тогда соотношение между сигналами при различном расположении пьезоэлектрической оси источника относительно электрического приемника будет:
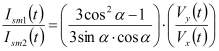 (3)
(3)
Для экспериментальной проверки результатов математического моделирования было проведено испытание описанного выше гипсового образца с единичным пьезоэлектрическим включением в различных конфигурациях. В первой серии экспериментов было установлено расстояние между точкой удара и приемником электрических сигналов, равное 20 мм. Во второй серии расстояние от точки удара до приемника составляло 30 мм. Удар производился по центру образца. Были проведены измерения при расположении плоскости ударник-приемник перпендикулярно и параллельно пьезоэлектрической оси пьезоэлемента.
При такой геометрии эксперимента угол (α) между направлением дипольного момента пьезоэлектрического элемента и радиус-вектором от источника до приемного датчика равен 310 при расстоянии от точки удара до приемника 20 мм и 22 0 при расстоянии 30 мм. В этом случае первый сомножитель в формуле (3) для расстояния 20 мм равен 0.96, а для расстояния 30 мм - 1.6.
На рисунке 2 приведены электрические сигналы, зарегистрированные из модельного образца, при различном направлении пьезоэлектрической оси пьезоэлектрического элемента относительно измерительного приемника при расстоянии от точки удара до приемника, равном 20 мм.
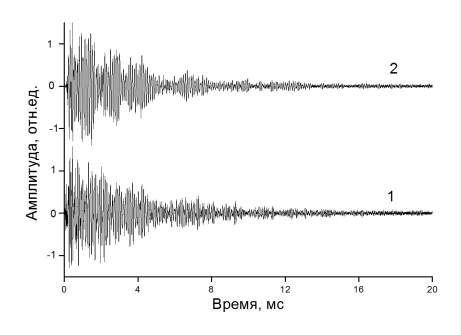
Рисунок 2. Электрические отклики из модели при расположении пьезоэлектрической оси пьезоэлектрического элемента: 1 - параллельно; 2 - перпендикулярно оси х.
Как видно из рисунка 2, величины электрических сигналов примерно одинаковы. Это более наглядно видно при сравнении энергетических спектров электрических откликов (рисунок 3).
|
|
|
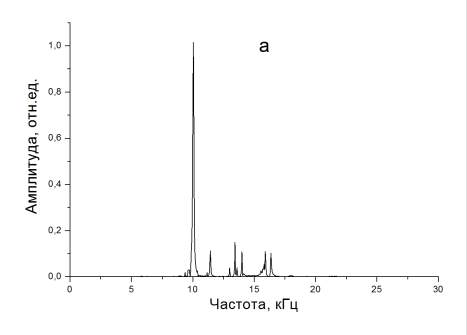
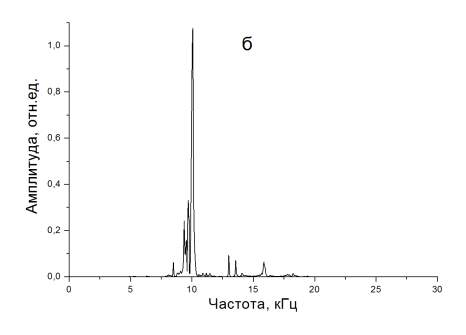
Рисунок 3. Энергетический спектр электрических откликов из модели при расположении пьезоэлектрической оси источника: а - параллельно; б - перпендикулярно оси x (при расстоянии между точкой удара и приемником 20 мм)
Из рисунка видно, что спектр электрического отклика имеет один ярко выраженный максимум на частоте порядка 10 кГц, что соответствует первой гармонике продольных акустических колебаний в данном образце. Остальные спектральные пики имеют значительно меньшую величину. При расстоянии от точки удара до приемника, равном 20 мм, первый сомножитель в формуле (3) равен 0.96, поэтому приблизительное равенство, как электрических откликов, так и наибольшего спектрального пика может свидетельствовать о равенстве или близком значении скоростей Vx и Vy при ударном возбуждении кубического образца.
На рисунке 4 приведены энергетические спектры при различном направлении пьезоэлектрической оси пьезоэлектрического элемента относительно измерительного приемника, при расстоянии от точки удара до приемника, равном 30 мм.
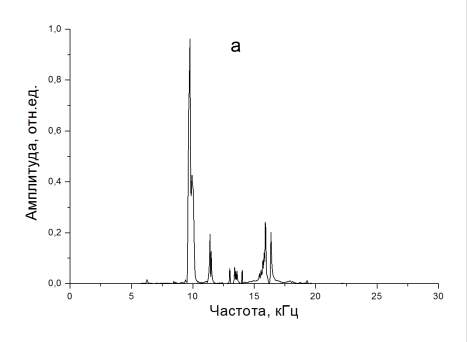
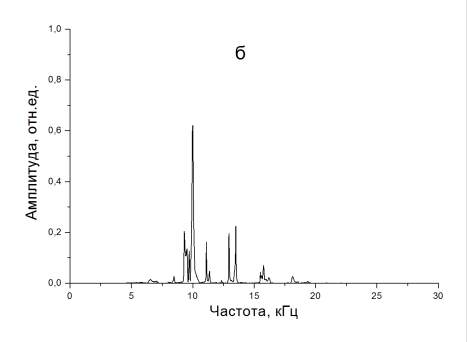
Рисунок 4. Энергетический спектр электрических откликов из модели при расположении пьезоэлектрической оси источника: а - параллельно; б - перпендикулярно оси x (при расстоянии между точкой удара и приемником 30 мм)
Как видно из рисунка, величина основного спектрального максимума при расположении плоскости ударник-приемник перпендикулярно пьезоэлектрической оси пьезоэлектрического элемента в 1.57 раза больше по сравнению с параллельным их расположением. Это хорошо согласуется с результатамирасчета при расстоянии 30 мм.
Следовательно, предложенная модель акустоэлектрических преобразований, вызванных импульсным ударным возбуждением пьезосодержащих диэлектрических материалов, достаточно хорошо согласуется с экспериментальными результатами.
Работа выполнена в рамках Государственного задания «Наука» (№ 7.1826.2011).
Рецензенты:
- Люкшин Борис Александрович, д.т.н., профессор, зав. кафедрой механики и графики Томского государственного университета систем управления и радиоэлектроники, г. Томск.
- Суржиков Анатолий Петрович, д.ф.-м.н., профессор, заместитесь директора по научной работе Института неразрушающего контроля Национального исследовательского Томского политехнического университета, г. Томск.