Безопасность технических систем всесторонне изучается в настоящее время целым рядом исследователей. Техногенный риск, в свою очередь, является основным количественным показателем безопасности систем.
В математическом моделировании риска превалирующей моделью является модель многомерной (не меньше двух компонент) случайной величины.
В данной статье рассмотрены результаты моделирования риска как функции случайных величин вероятности исходных событий аварий Q и ущерба от них C при их линейной связи.
Постановка задачи
Рассмотрим риск R, вероятность исходных событий аварий Q и ущерб C как случайные величины (СВ).
Допустим, что ущерб есть функция вероятности исходных событий:
c = α(q),
при этом вероятность Q - есть СВ с плотностью распределения fQ(q), а СВ R связана с Q и C функциональной зависимостью R = Q·C. Требуется найти закон распределения величины R.
Модель риска
Если α (q) является непрерывной, дифференцируемой, монотонной и имеет обратную функцию α-1, то функция распределения СВ ущерба от неблагоприятного события при монотонно убывающей α примет вид:
|
FC (c) = P (C<c) = P ( q < Q ≤ 1 ) = |
|
= 
,
где fQ (q) - плотность распределения СВ вероятность исходного события с областью определения
|
W1 : |
(1) |
Отсюда плотность распределения С равна для α монотонно убывающей:
|
fC (c) = |
(2) |
= - fQ 
[α-1 (c)] .
Найдем плотность распределения ущерба в случае его линейной зависимости от вероятности исходных событий
|
c = α(q) = -k1q + k0 , |
(3) |
где k0 и k1 - коэффициент смещения и угловой коэффициент линейной зависимости соответственно.
Тогда условная плотность вероятности ущерба при линейной зависимости C от Q согласно (2) связана с плотностью распределения Q:
|
fC/Q (c) = fQ |
(5) |
, k1 ≠ 0.
Далее функция распределения риска равна
|
FR (q,c) =
= |
(6) |
= 
fQ ·fQ (q) dc dq =
Так как область интегрирования задается выражением (1), то
|
|
(7) |
.
Поскольку r = q·c = q·α(q), преобразуем формулу (7) к виду, содержащему переменную r:
|
|
(8) |
, k1 > 0,
откуда после дифференцирования по r следует выражение для плотности распределения риска fR :
|
|
(9) |
, k1 > 0.
В соответствии с (9) получены выражения для плотности вероятности риска при различных распределениях случайной величины вероятности, которые приведены в табл. 1.
Таблица 1 Вид зависимостей плотности распределения риска при различных законах распределения СВ Q
|
Функция линейной зависимости ущерба от вероятности |
|
|
c = α(q) = -k1q + k0 |
|
|
Распределение СВ вероятности Q |
Функция плотности распределения риска fR (r) |
|
Нормальное |
k1 > 0. |
|
Логарифмически нормальное |
|
|
Вейбулла |
|
|
Экспоненциальное |
|
|
Рэлея |
|
|
Стьюдента |
|
|
Усеченное нормальное |
k1 > 0. |
,
, k1 > 0.
, k1 > 0.
, k1 > 0.
, k1 > 0.
, k1 > 0.
Выбор законов распределения СВ вероятности обусловлен практикой исследований в сфере безопасности технических систем [3,5]. Распределения Гаусса (нормальное), логарифмически нормальное, Вейбулла, Рэлея описывают развитие отказов и дефектов в различных технических системах (например, различные элементы ядерных реакторов, коррозия металлов, наработка на отказ электронных элементов). Нетрадиционное для подобных задач распределение Стьюдента взято потому, что обладает тяжелыми хвостами, более соответствующими поведению «редких» аварийных событий.
План модельного эксперимента для определения значений вероятности Q, распределенной по закону Вейбулла, приведен в табл.2.
Таблица 2 Значения параметров плотности распределения вероятности Q
|
|
Угловой коэффициент k1 |
Коэффициент смещения k0 |
Коэффициент λq |
Коэффициент αq |
||||||||
|
1 |
10^7 |
10^5 |
10^- 4 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
2 |
|
|
10^- 5 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
3 |
|
|
10^- 6 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
4 |
|
|
10^- 7 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
5 |
10^8 |
10^5 |
10^- 4 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
6 |
|
|
10^- 5 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
7 |
|
|
10^- 6 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
8 |
|
|
10^- 7 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
9 |
10^10 |
10^6 |
10^- 4 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
10 |
|
|
10^- 5 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
11 |
|
|
10^- 6 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
12 |
|
|
10^- 7 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
13 |
10^11 |
10^6 |
10^- 4 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
14 |
|
|
10^- 5 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
15 |
|
|
10^- 6 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
|
16 |
|
|
10^- 7 |
0,1 |
0,5 |
0,9 |
1,1 |
1,5 |
1,9 |
2,1 |
2,5 |
2,9 |
При выборе параметров распределений авторы руководствовались следующими соображениями. Для распределения Вейбулла значения λq от 10 -4 и ниже, т.к. события считаются редкими, а значения αq взяты во всех трех интервалах: (0;1), (1;2), (2;∞). (см., например, [4]). Коэффициенты линейной зависимости оценены на основании данных [1].
Результаты моделирования и их анализ
Модельный эксперимент проведен на ЭВМ в среде вычислительного пакета Maple.
1. В статье приведены полученные значения функции плотности вероятности риска fR(r) для распределения вероятности исходных событий по закону Вейбулла. Поведение функций плотности риска иллюстрируют приведенные диаграммы в логарифмическом и обычном масштабах (рис.1-5).
Рис. 1. Плотность распределения риска при 0< αq <1
Рис. 2. Плотность распределения риска при 1< αq <2 и при 2< αq <3
Рис. 3. Зависимость плотности распределения риска от значения 0< αq <1
при k1=107, k0=105 , λq = 10-7
Рис. 4. Зависимость плотности распределения риска от значения 1< αq <2
при k1=107, k0=105 , λq = 10-4
Рис. 5. Зависимость плотности распределения риска от значения 0< αq <1
при k1=1011, k0=106 , λq = 10-4
2. Данное исследование выполнялось в рамках гранта РФФИ (проект 11-01-00008). Исследовано влияние значений параметров закона распределения вероятности αq и λq и коэффициентов линейной зависимости k1 и k0 на поведение функции плотности распределения риска fR(r). При этом значения функций fR(r) табулированы на интервале [0;57], но в данной статье приводятся не полностью из-за ограниченности объема публикации.
3. Анализ результатов при распределении вероятности по закону Вейбулла
Проанализируем влияние параметров распределения СВ Q и линейной зависимости на свойства плотности распределения риска. Рассмотрим отдельно поведение функции плотности риска на интервалах по параметру α: (0;1), (1;2), (2;4).
1) Функция плотности распределения риска fR(r) медленно возрастает (рис.1) при αq (0;1) и медленно убывает (рис.2) при αq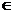 
(1;2) и αq 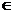(2;4).
2) При увеличении значения параметра αq от меньшего к большему на каждом интервале по αq значения функции уменьшаются по величине на 1-2 порядка (рис.4), и скорость роста функции замедляется (рис.3).
3) При увеличении коэффициентов линейной зависимости k1 и k0 увеличивается разница между значениями функции до 3-4 порядков (рис.5) при изменении αq.
4) При прочих фиксированных параметрах изменение λq (уменьшение на порядок в интервале от λq =10-4 до λq =10-7 ) приводит к уменьшению значений функции плотности ровно на 2 порядка (почти без изменения мантиссы) (табл. 3).
Таблица 3 Изменение значений функции плотности при уменьшении λq
|
при k1=1011, k0=106, αq =0,1 |
||||
|
|
f R (r ) |
|||
|
r |
λ=10^(-4) |
λ=10^(-5) |
λ=10^(-6) |
λ=10^(-7) |
|
0 |
1,75732E-14 |
1,75746E-16 |
1,75748E-18 |
1,75748E-20 |
|
1 |
1,75808E-14 |
1,75821E-16 |
1,75823E-18 |
1,75823E-20 |
|
2 |
1,75883E-14 |
1,75897E-16 |
1,75898E-18 |
1,75898E-20 |
|
3 |
1,75958E-14 |
1,75972E-16 |
1,75973E-18 |
1,75974E-20 |
|
4 |
1,76033E-14 |
1,76047E-16 |
1,76049E-18 |
1,76049E-20 |
|
|
|
|
|
|
|
при k1=1011, k0=106, αq =1,1 |
||||
|
|
f R (r ) |
|||
|
r |
λ=10^(-4) |
λ=10^(-5) |
λ=10^(-6) |
λ=10^(-7) |
|
0 |
1,9086E-19 |
1,90863E-21 |
1,90863E-23 |
1,90864E-25 |
|
1 |
1,90858E-19 |
1,90861E-21 |
1,90863E-23 |
1,90861E-25 |
|
2 |
1,90856E-19 |
1,90859E-21 |
1,90859E-23 |
1,90859E-25 |
|
3 |
1,90854E-19 |
1,90857E-21 |
1,90857E-23 |
1,90857E-25 |
|
4 |
1,90852E-19 |
1,90855E-21 |
1,90855E-23 |
1,90855E-25 |
|
|
|
|
|
|
|
при k1=1011, k0=106, αq =2,1 |
||||
|
|
f R (r ) |
|||
|
r |
λ=10^(-4) |
λ=10^(-5) |
λ=10^(-6) |
λ=10^(-7) |
|
0 |
1,26711E-24 |
1,26715E-26 |
1,26715E-28 |
1,26715E-30 |
|
1 |
1,2671E-24 |
1,26714E-26 |
1,26714E-28 |
1,26714E-30 |
|
2 |
1,26709E-24 |
1,26713E-26 |
1,26713E-28 |
1,26714E-30 |
|
3 |
1,26708E-24 |
1,26712E-26 |
1,26713E-28 |
1,26713E-30 |
|
4 |
1,26708E-24 |
1,26712E-26 |
1,26712E-28 |
1,26712E-30 |
Сравнительный анализ таблицы 3 показывает зависимость значений функции плотности распределения риска от изменений интервала по параметру αq. Переход по интервалам значений αq сопровождается уменьшением значений fR (r) на 5 порядков.
Заключение
Таким образом, в статье получены следующие результаты:
- новые аналитические выражения для определения плотности распределения риска при линейно зависимых случайных величинах вероятности исходных событий и ущерба;
- найдены численные значения функции плотности fR (r) для различных законов распределения случайной величины Q;
- проведен анализ влияния значений параметров распределения СВ Q на характеристики плотности вероятности риска.
Работа выполнена при поддержке гранта РФФИ (проект 11-01-00008)
Рецензенты:
- Галкин Валерий Алексеевич, доктор физико-математических наук, профессор, заведующий кафедрой прикладной математики Обнинского института атомной энергетики научно-исследовательского ядерного университета МИФИ Министерства образования и науки Российской Федерации, г. Обнинск.
- Григорьев Леонид Иванович, доктор технических наук, профессор, заведующий кафедрой автоматизированных систем управления Российского государственного университета имени И. М. Губкина Министерства образования и науки Российской Федерации, г. Москва.