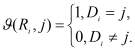В настоящее время одним из развивающихся и перспективных направлений в цифровой обработке изображений является применение фрактального анализа. Фракталы обладают свойствами самоподобия, что означает точное или вероятностное повторение свойств объекта при рассмотрении его в разных масштабах. Свойство самоподобия приводит к определенным закономерностям в статистическом поведении признаков изображений, в результате чего изображения можно с определенной точностью описать фрактальными признаками [1,2,7,8].
Любая из процедур обработки изображений опирается на модель класса изображений - формализованное описание, выполненное с определенной степенью абстрагирования. Роль модели изображения в процессе извлечения информации состоит в обеспечении адекватного описания существенных свойств класса изображений, позволяющего дать конструктивную основу, для построения эффективных вычислительных процедур.
В частности, для создания новых методов фрактальной обработки изображений необходимо создать фрактальную модель изображений. Так как для построения фракталов используются системы итерируемых функций [3,7,8], то одним из возможных способов описания изображения является использование для этого систем итерируемых функций [4-6].
Фрактальная модель изображения, описанная в [4-6], позволяет вычислить локальные признаки самоподобия, их проявление и изменение на изображении. Эти признаки показывают, какие участки изображения участвуют в его формировании, т.е. согласно распределению самоподобия внутри изображения можно выявить участки, используя которые можно воспроизвести изображение с наибольшей точностью. Более подробно о вычислении локальных признаков самоподобия описано в [5,6].
Характер распределения самоподобия цифрового изображения
Представление изменения самоподобия участков изображения с помощью изолиний обладает наглядностью и позволяет качественно оценить распределение, но не позволяет получить количественную оценку. Для задач обработки изображений необходимо представить распределение самоподобия в виде характеристик, имеющих числовое или аналитическое выражение.
Для этого строится гистограмма использования доменных блоков 
(рис. 1):
|
|
(1) |
,
Чем больше значение 
для доменного блока 
, тем более характерным является участок для этого изображения. Т.е. точность описания изображения с помощью характерных участков будет наивысшей. Следовательно, такие участки можно использовать как шаблоны изображений в задаче распознавания и классификации изображений.
Если значения гистограммы 
упорядочить по убыванию, то в общем виде получится следующего вида кривая (рис. 2):
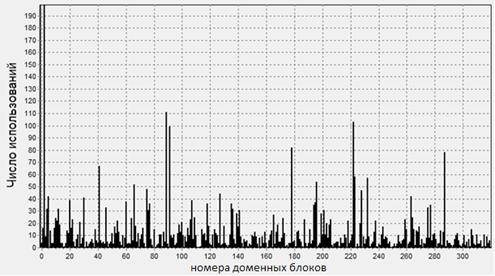
Рис.1. Гистограмма количества использования доменных блоков во фрактальном коде изображения
Рис. 2. Аппроксимация характера распределения самоподобия на тестовом изображении
График, представленный на рисунке 2, отражает характер распределения самоподобия на изображении. Если аппроксимировать полученные значения, можно получить аналитическое выражение, характеризующее распределение признаков самоподобия.
Наибольшее соответствие наблюдается при аппроксимации логарифмическим уравнением вида (рис. 2):
|
|
(2) |
,
Таким образом, предлагаются новые признаки изображений, характеризующие внутреннее распределение самоподобия и наиболее подобные участки изображения. Распределение самоподобия 
дает возможность использовать в качестве информативных признаков изображения наиболее характерные его участки, полученные на основе гистограммы 
, которые в большинстве случаев являются уникальными для каждого изображения или класса изображений, и коэффициенты уравнения k и b, описывающего характер распределения локальных признаков самоподобия.
Вычисление характерных участков цифровых изображений
Можно предположить, что два изображения одного класса описываются одинаковыми участками, и наиболее самоподобные области одного изображения данного класса должны встречаться в других изображениях данного класса.
Исходя вышесказанного, можно говорить об участках изображения - доменных блоках, которые наиболее часто встречаются на изображении или с помощью которых можно с наибольшей точностью описать изображение. Здесь наиболее часто используемые доменные блоки являются наиболее характерными участками изображения. Пример характерных участков представлен на рис. 3.
Рис. 3. Характерные участки тестовых изображений микроструктур металлов
Алгоритм формирования списка таких участков следующий. Вначале производится вычисление фрактальных параметров изображения с использованием всех доменных блоков. Вычисляется максимальная ошибка аппроксимации ранговых блоков:
|
|
(3) |
.
При вычислении фрактальных параметров с использованием всех доменных блоков ошибка 
является минимальной. Определяется доменный блок, который встречается на изображении максимальное количество раз. Он записывается в список характерных участков и исключается из списка доменных блоков. Затем осуществляется повторное формирование фрактального кода, при этом доменный блок, который встречается на изображении максимальное количество раз, также записывается в список характерных участков. Так как на предыдущей итерации из списка доменных блоков был удален характерный участок, то ошибка описания изображения оставшимися доменными блоками возрастет. Так повторяется до тех пор, пока ошибка описания не будет значительно выше минимальной. В конечном итоге получается список характерных участков изображения, наиболее точно его описывающих.
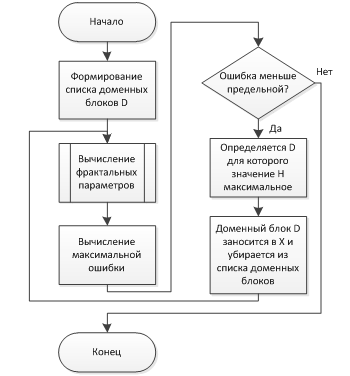
Рис. 4. Блок-схема алгоритма формирования характерных участков
Таким образом, каждое изображение характеризуется вектором характерных участков 
. Под характерным участком изображения понимается доменный блок, число раз использования которого во фрактальном коде больше, чем значение 
:
|
|
(4) |
.
Полученные характерные участки цифрового изображения являются новым фрактальным признаком, который можно использовать в различных задачах цифровой обработки изображений.
Исследование характерных участков для изображений одного и разных классов
Характерные участки изображения представляют собой часто встречаемые блоки и блоки, которым подобно некоторое количество остальных участков изображения. Следовательно, для одного класса изображений характерные участки должны быть в наибольшей степени равны.
Для сравнения характерных участков будем использовать следующие параметры.
Стандартное отклонение:
|
|
(5) |
где μ - среднее значение яркостей точек блока размером 
, 
- значение яркости точки блока с координатами 
.
Межпиксельная контрастность, которая измеряет среднюю разность между значениями соседних пикселей в восьмисвязной окрестности:
|
|
(6) |
Бета, которая показывает, насколько сильно отличаются значения яркостей точек блока от значения яркости средней точки:
|
|
(7) |
Для исследования были взяты текстурные изображения трех классов, состоящих из пяти подклассов каждый. Всего 75 изображений: по пять изображений в каждом подклассе. Для каждого изображения были вычислены характерные участки, по пять для каждого изображения: всего 375 участков. Для каждого характерного участка были вычислены параметры (5-7).
Использование вычисленных параметров характерных участков в большинстве случаев при рассмотрении по отдельности не предоставляют возможность проводить классификацию изображений, так как значения параметров очень близки для разных участков. Однако использование параметров в совокупности позволяет использовать данные признаки для задач классификации изображений.
Внутри класса СКО параметров характерных участков не превышает 15 %, что дает основание использовать их для сравнения изображений.
Исследование характера распределения самоподобия для изображений одного и разных классов
Характер распределения самоподобия цифрового изображения описывает использование самоподобных участков при описании изображения. Фактически он отражает фрактальность изображения.
Для использования этого признака в качестве информативного признака необходимо провести исследование характера распределения самоподобия, заключающееся в сравнении признака изображений одного и разных классов.
Для исследования были взяты текстурные изображения трех классов, состоящих из пяти подклассов каждый. Всего 75 изображений: по пять изображений в каждом подклассе.
В результате исследования было установлено, что средние значения коэффициентов k и b для изображений разных подклассов различаются, об этом свидетельствуют средние значения параметров. В то время как внутри класса наблюдается устойчивость параметров, о чем говорят величины СКО.
Таким образом, подтверждается возможность использования характера распределения самоподобия в качестве классифицирующего признака. Среднее значение СКО признака внутри класса не превышает 10 %. Однако коэффициенты уравнения разных классов в некоторых случаях различаются недостаточно для того, чтобы говорить о точной классификации, поэтому необходимо использовать данный фрактальный признак совместно с другими признаками для достижения более точных результатов.
Заключение
Исследование характера распределения самоподобия показало, что для изображений разных подклассов наблюдаются разные значения признака, в то время как внутри класса наблюдается устойчивость параметров. Таким образом, подтверждается возможность использования характера распределения самоподобия в качестве классифицирующего признака. Однако коэффициенты уравнения разных классов в некоторых случаях различаются недостаточно для того, чтобы говорить о точной классификации, поэтому необходимо использовать данный фрактальный признак совместно с другими признаками для достижения более точных результатов.
Характерные участки являются участками, наиболее полно описывающими свойства исходного изображения. Установлено, что для разных изображений характерные участки также отличаются. Поэтому можно говорить о характерных участках как о классифицирующем признаке. Это подтверждают проведенные исследования, согласно которым характеристики характерных участков разных классов различаются, в то время как свойства характерных участков изображений одного класса являются примерно равными. Поэтому можно сделать вывод о возможности применения данных признаков для решения задач классификации и сравнения изображений.