
Рис. 1. Квадротор MicroDrones GmbH
Удобство управления квадротором заключается в том, что для поступательного движения не требуется шарниров, перемещающих вращающиеся конструкции. Движение вперед и назад, вправо и влево осуществляется за счет разности тяг двух противоположных винтов (см. рис. 2). В квадроторе нет необходимости в угле рыскания, так как движение по боковой оси абсолютно идентично движению по продольной оси по отношению к собственным осям симметрии. За счет вращения каждой пары винтов в противоположную сторону в квадроторе отсутствует реакция корпуса на общую тягу винтов, поэтому нет необходимости в компенсационном моменте, вырабатываемым в обычных вертолетах дополнительным хвостовым винтом. Квадротор может стоять неподвижно в пространстве, что также является дополнительным преимуществом, позволяющим использовать его в режиме робота.
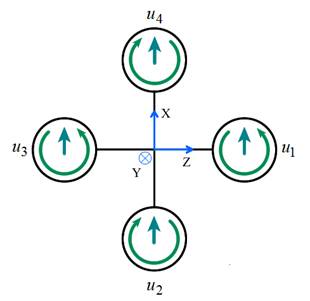
Рис. 2. Схема управления квадротором
Сегодня квадроторы широко используются и продаются по всему миру. На настоящем этапе развития основным направлением является их интеллектуализация. Большинство работающих квадроторов и практически всех беспилотных летающих аппаратов управляется человеком от пульта управления. Автономные режимы работы для летающих роботов встречаются крайне редко.
Данное обстоятельство вызвано, прежде всего, сложностью реализации систем управления, которая помимо обеспечения режима движения летающего робота должна также выполнять функцию выбора. Достаточно сложно реализовать полностью автономную систему управления летающим роботом, которая бы обеспечила весь процесс полета.
Реально полет летающего робота должен включать несколько режимов управления, например, стабилизацию робота в пространстве, перемещение его в другую точку пространства, обнаружение и облет препятствий, обеспечение режима посадки. Перечисленные режимы движения могут быть легко реализованы достаточно несложными системами управления, но тогда при автономном режиме полета возникает дополнительная проблема выбора режима полета. Летающий робот должен автономно принять решение по выбору критерия, минимум которого ему необходимо обеспечивать. По критерию уже можно отобрать режим полета, хотя и при этом остается вопрос о том, что необходимо делать при ошибочном принятии решения.
Выбор решения формально описывается с помощью логических выражений, следовательно, система управления должна включать не только набор блоков управления, реализующих определенные режимы управления, но и блоки логического вывода, которые также по состоянию объекта должны определить выбор режима управления. Из сказанного следует, что для управления летающими роботами актуальна задача синтеза логико-функционального управления.
Рассмотрим формальную постановку задачи синтеза логико-функциональной системы управления.
Задана система дифференциальных уравнений, описывающая динамику объекта управления
![]() , (1)
, (1)
где ![]() - вектор состояния объекта управления,
- вектор состояния объекта управления, ![]() ,
, ![]() - вектор управления,
- вектор управления, ![]() .
.
На управление наложены ограничения
![]() , (2)
, (2)
где U - ограниченное замкнутое множество.
Заданы начальные условия
![]() . (3)
. (3)
Задан критерий качества управления в виде функционала
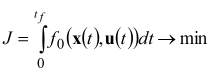 , (4)
, (4)
где ![]() - время окончания процесса управления.
- время окончания процесса управления.
Чтобы минимизировать значение функционала (4), необходимо найти управление в виде
![]() , (5)
, (5)
где ![]() - вектор логических переменных,
- вектор логических переменных, ![]() ,
, ![]() ,
, ![]() .
.
Логические переменные определяют выбор вариантов управления на основе предикатной функции, которую также необходимо найти
![]() , (6)
, (6)
где ![]() .
.
Для решения задачи используем метод сетевого оператора [1-8]. Метод позволяет искать решения на множестве математических выражений, задаваемых целочисленной матрицей сетевого оператора. Поскольку в задаче необходимо помимо обычного функционального управления (5) искать также логическое управление (6), то используем два сетевых оператора. Для синтеза предикатной функции (6) используем логический сетевой оператор [6].
Логическую функцию ищем с помощью метода логического сетевого оператора. Функцию дискретизации определяем на основе анализа конкретной задачи.
Для поиска решения используем генетический алгоритм, построенный на основе принципа базисного решения. Для определения сетевого оператора, к которому необходимо применить вариации, в генетическом алгоритме используем дополнительный бинарный вектор.
В качестве примера рассмотрим синтез логико-функциональной системы управления для беспилотного вертолета типа квадротора.
Математическая модель квадротора имеет следующий вид
![]() ,
, 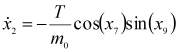 ,
, ![]() ,
,
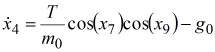 ,
, ![]() ,
, 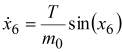 ,
,
![]() ,
, 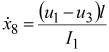 ,
, ![]() ,
, 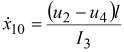 ,
,
где ![]() ,
, ![]() ,
, ![]() - координаты центра масс,
- координаты центра масс, ![]() - продольная дальность,
- продольная дальность, ![]() - высота,
- высота, ![]() - боковая дальность,
- боковая дальность, ![]() ,
, ![]() ,
, ![]() - соответствующие проекции вектора скорости движения центра масс,
- соответствующие проекции вектора скорости движения центра масс, ![]() ,
, ![]() - углы поворота вокруг горизонтальной плоскости,
- углы поворота вокруг горизонтальной плоскости, ![]() ,
, ![]() - соответствующие углы скорости,
- соответствующие углы скорости, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - тяги винтов,
- тяги винтов, ![]() ,
, ![]() - расстояние между противоположными винтами,
- расстояние между противоположными винтами, ![]() ,
, ![]() - моменты инерции относительно осей в горизонтальной плоскости,
- моменты инерции относительно осей в горизонтальной плоскости, ![]() - масса квадротора,
- масса квадротора, ![]() - ускорение свободного падения.
- ускорение свободного падения.
На управление наложены ограничения
![]() ,
, ![]() .
.
где ![]() и
и ![]() заданы величины минимальной и максимальной тяг винтов.
заданы величины минимальной и максимальной тяг винтов.
Для того чтобы обеспечить отсутствие вращения вокруг вертикальной оси, тяги винтов должны удовлетворять соотношению
![]() .
.
Для управления движением квадротора используем наклоны плоскости вращения винтов, которые определяются углами ![]() и
и ![]() . На величины углов наложены ограничения
. На величины углов наложены ограничения
![]() ,
,
![]() .
.
Пространственная траектория задана набором точек
![]() ,
,
где M - количество точек пространственной траектории.
Необходимо найти управление, чтобы минимизировать две целевые функции. Первая функция определяет точность движения по траектории. Вторая функция определяет время прохождения траектории.
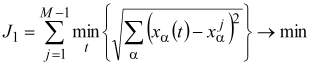 ,
,
![]() ,
,
где
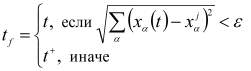 ,
, ![]() .
.
Целью управления является движение квадротора по пространственной траектории, которая должны была миновать препятствия, поэтому обе целевые функции штрафовались в случае не попадания квадротора в окрестность какой-либо точки пространственной траектории и при попадании на область препятствия.
При расчетах использовали модель со следующими параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Траектория движения содержала восемь точек
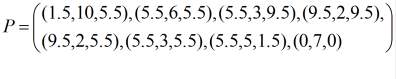
Были также определены препятствия в виде набора угловых точек на горизонтальной плоскости
![]() ,
,
где K - число препятствий, Ci - координаты углов
![]()
Всего было рассмотрено четыре препятствия с координатами
![]()
![]()
![]()
![]()
Задача логического управления заключалась в обеспечении переключения точек пространственной траектории. Для построения логического выражения на вход логического блока подавались отклонения состояния объекта от текущей целевой точки заданной траектории и следующей точки. Начальные значения для моделирования были нулевые при высоте ![]() м.
м.
Результаты моделирования с одним из полученных логико-функциональных управлений приведены на рис. 3-5. На рисунках показаны квадратные точки пространственной траектории. На рис. 3 изображены учитываемые при синтезе области препятствий в форме прямоугольников.
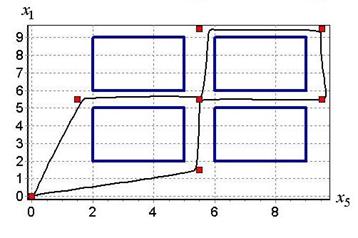
Рис. 3. Проекция траектории на горизонтальную плоскость
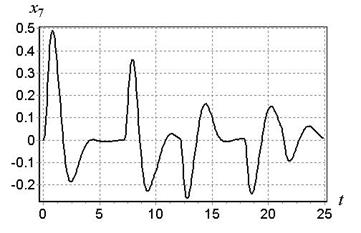
Рис. 4. Изменение угла x7
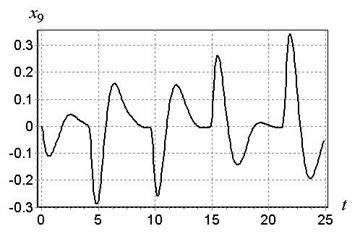
Рис. 5. Изменение угла x9
По результатам моделирования видно достаточно точное движение квадротора по заданным точкам траектории. Прохождение всей траектории составило 25 с, при этом квадротор не задел область препятствий.
Рецензенты:
Гурченков А. А., д.ф.-м.н., профессор, ведущий научный сотрудник отдела сложных систем Федерального государственного бюджетного учреждения науки Вычислительного центра им. А. А. Дородницына Российской академии наук, г. Москва.
Забудский Е. И., д.т.н., профессор кафедры электроснабжения и электрических машин Федерального государственного бюджетного образовательного учреждения высшего профессионального образования Московского государственного агроинженерного университета им. В. П. Горячкина, г. Москва.



