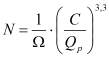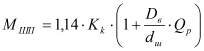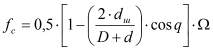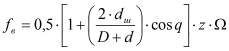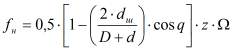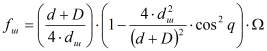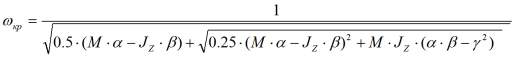, (1)
где H - кинетический момент маховика; J - момент инерции маховика; 
- угловое ускорение вращения маховика.
В общем виде УДМ представляет собой массивный ротор с явно выраженным ободом 1 (маховик), установленный в опорах 2 и приводимый во вращение электродвигателем 3, ротор которого закреплен на маховике, а статор - на основании 4. Для снижения момента сопротивления вращению маховика и, следовательно, снижения энергопотребления, вся конструкция помещена в герметичную камеру, образованную кожухом 5 и основанием [3].
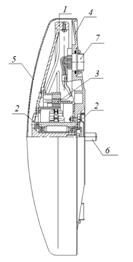
Рис. 1. Конструкция УДМ
При проектировании УДМ руководствуются математической моделью, представляющей взаимосвязь его эксплуатационных характеристик. Но в связи с тенденциями совершенствования характеристик ИО в части увеличения угловой скорости вращения, срока активного существования и уменьшения массогабаритных характеристик необходима корректировка модели.
Уменьшение массогабаритных характеристик приводит к уменьшению жесткости основных элементов, что ведет за собой уменьшение собственных резонансных частот и критической скорости вращения ИО, следствием чего является проявление вибрации его конструкции.
Для одновременного увеличения скорости вращения и срока активного существования ИО необходимо на этапе проектирования шарикоподшипникового узла осуществлять выбор подходящего подшипника и оценивать уровень его вибрации при работе на предполагаемой угловой скорости вращения ИО.
Шарикоподшипниковый узел (и непосредственно шарикоподшипник) - основной источник смещения центра масс и вибрации маховика. Спектр вибрации шарикоподшипников состоит из многочисленных гармоник, причем некоторые из них имеют высокие уровни по амплитуде. Вибрация подшипников определяется случайными взаимодействиями геометрически неидеальных поверхностей дорожек качения и шариков. Возможны выбросы энергии, обусловленные внезапными проскальзываниями шариков и их резким проворачиванием под действием гироскопических моментов, что оказывает влияние на колебание момента инерции и, вследствие этого, колебание исходного положения кинетического момента [4, 5].
Поэтому необходимо расширить математическую модель в части добавления формул по теоретическому определению частот основных дефектов шарикоподшипникового узла. Все гармонические составляющие вибрации от подшипников качения (элементов подшипника) имеют частоты, связанные с угловой скоростью вращения ИО (внутреннего кольца подшипника).
Обобщенная скорректированная математическая модель УДМ:
|
1 |
|
кинетический момент; |
|
|
|
|
|
2 |
|
масса маховика; |
|
|
|
|
|
3 |
|
ресурс; |
|
|
|
|
|
4 |
|
потребляемая мощность; |
|
|
|
|
|
5 |
|
момент сопротивления; |
|
|
|
|
|
6 |
|
управляющий момент маховика; |
|
|
|
|
|
7 |
|
время разгона; |
|
|
|
|
|
8 |
|
момент трения шарикоподшипников; |
|
|
|
|
|
9 |
|
момент аэродинамического сопротивления; |
|
|
|
|
|
10 |
|
аэродинамические коэффициенты для ламинарного и турбулентного течения; |
|
11 |
|
|
|
|
|
|
|
12 |
|
частота вибрации, вызванная неуравновешенностью сепаратора подшипника; |
|
|
|
|
|
13 |
|
частота вибрации, вызванная дефектом внутреннего кольца подшипника; |
|
|
|
|
|
14 |
|
частота вибрации, вызванная дефектом наружного кольца подшипника; |
|
|
|
|
|
15 |
|
частота вибрации, вызванная дефектом тела качения подшипника; |
|
|
|
|
|
16 |
|
частота вибрации, вызванная шероховатостью или овальностью тел качения подшипника; |
|
|
|
|
|
17 |
|
частота вибрации, вызванная зазором в подшипнике; |
|
|
|
|
|
18 |
|
частота вибрации, вызванная периодическими изменениями жесткости подшипника при перекатывании тел качения; |
|
|
|
|
|
19 |
|
частота вибрации, вызванная зазорами в гнездах сепаратора подшипника; |
|
|
|
|
|
20 |
|
критическая угловая скорость вращения УДМ; |
|
|
|
|
|
21 |
|
вынужденные колебания, возникающие по двум ортогональным осям УДМ, |
|
22 |
|
|
|
|
|
|
где R - наружный радиус маховика; r - внутренний радиус маховика; k=R/r; 
- удельная масса материала маховика; h - высота обода; D - диаметр маховика; Ω - угловая скорость вращения; С - коэффициент работоспособности подшипников; Qр - нагрузка; Kk - коэффициент трения качения; Dв - внутренний диаметр наружного кольца шарикоподшипника; ρ - плотность среды, окружающей маховик; Re - число Рейнольдса; D - диаметр наружного кольца подшипника; d - диаметр внутреннего кольца подшипника; z - количество тел качения (шариков); dш - диаметр тела качения (шарика); q - угол контакта тел качения; dср - диаметр окружности центров шариков; nв - число волнистостей по окружности беговой дорожки качения внутреннего или наружного кольца.
Экспериментальные исследования показали, что вибрационная характеристика (ВХ) УДМ (рис. 2) далека от теоретической - в рабочем диапазоне угловых скоростей вращения появляются резонансы, которые неминуемо влияют на динамику механической системы всего КА. Первый резонансный диапазон 26,6 - 45 с-1, второй - 70 - 100 с-1.
Для определения вибрационной картины шарикоподшипникового узла УДМ разработана методика частотного анализа, основанная на создании программного модуля анализа виброактивного спектра УДМ, являющегося дополнением к программному обеспечению PULSE Lab Shop модульной многоканальной системы анализа сигналов PULSE фирмы Bruel&Kjaer (Дания).
В системе анализа сигналов PULSE удачно сочетаются одновременно мощь современного анализатора, использующего специализированное программное обеспечение, и широкие вычислительные возможности персональной ЭВМ. Система предназначена для сбора данных с метками времени, измерений общего уровня шума и вибрации, базового и расширенного акустического анализа, анализа динамических характеристик конструкций, диагностики механических устройств, электроакустических испытаний [1].
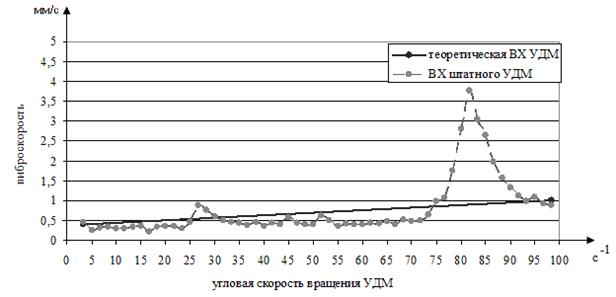
Рис. 2. Вибрационная характеристика УДМ
Временные спектры измерений сохраняются в мультибуфере анализатора, а частотные выводятся в рабочее пространство программы PULSE Lab Shop в виде графиков трех переменных: частоты анализатора, уровня виброскорости, угловой скорости вращения УДМ (рис. 3) [2].
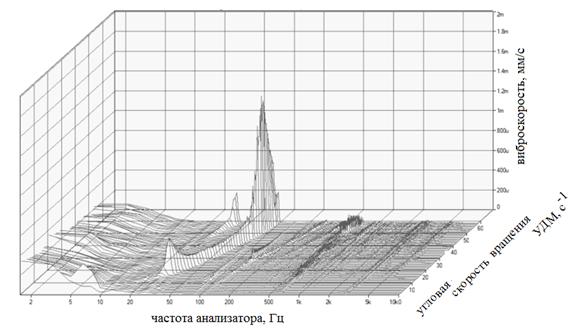
Рис. 3. Трехмерный спектр вибрации УДМ в зоне шарикоподшипникового узла
На графике представлены спектры вибрации УДМ в диапазоне угловых скоростей вращения от 0 до 100 с-1.
Разработанный программный модуль позволяет в автоматическом режиме формировать таблицу разложения спектра вибрации, состоящую из частот спектра, амплитудные значения виброскорости которых превышают поровое значение в 65 дБ
(0,087 мм/с). Уровень порогового значения обусловлен требованиями, предъявляемыми к подшипникам качения, используемым в конструкции УДМ.
Сведенные в таблицу данные далее обрабатываются в следующей последовательности:
- просматриваются спектры вибрации на каждой угловой скорости вращения УДМ;
- указываются частотные диапазоны появления экстремумов в спектре вибрации;
- посредством созданного макроса с помощью программы Visual Basic, при указании диапазонов частот спектра и нажатии активной кнопки «Выделение диапазонов и максимальных пиков» (рис. 4) осуществляется выделение угловых скоростей вращения (подчеркнутые, выделенные курсивом) и частот с максимальным уровнем виброскорости (выделенные полужирным шрифтом и курсивом).
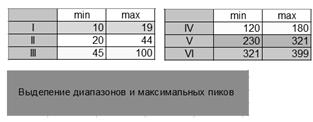
Рис. 4. Указание частотных диапазонов в программном модуле анализа виброактивного спектра УДМ
В табл. 2 представлено разложение спектра вибрации первого резонанса в частотной области 26,6 - 45 с-1 герметичного УДМ, ВХ которого представлена на рис. 2.
Из представленной таблицы видно, что максимальное значение по амплитуде виброскорости имеет частота 29,69 Гц, амплитудное значение виброскорости которой превышает уровень угловой скорости вращения. Следовательно, первый резонанс возникает на частоте анализатора 29,69 Гц.
Для проведения частотного анализа дефектов шарикоподшипникового узла в модель виброактивного анализа спектра включены:
- таблица основных параметров диагностируемого подшипника качения;
- расчетные таблицы возможных дефектных частот подшипника (и их гармоник) на каждой угловой скорости вращения УДМ;
- таблица сравнения выявленной частоты из спектра вибрации УДМ с расчетной дефектной частотой с погрешностью 15 %.
Табл. 2
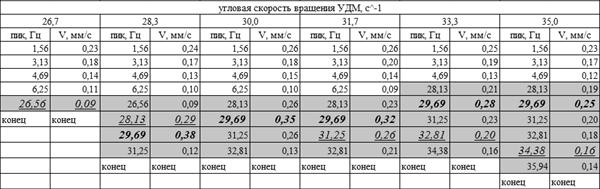
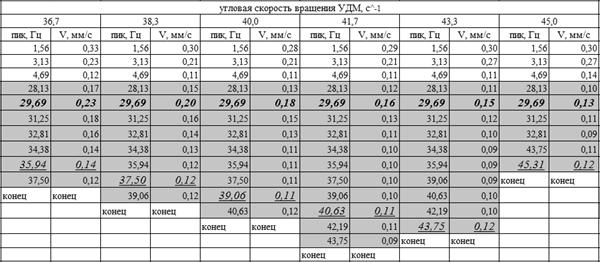
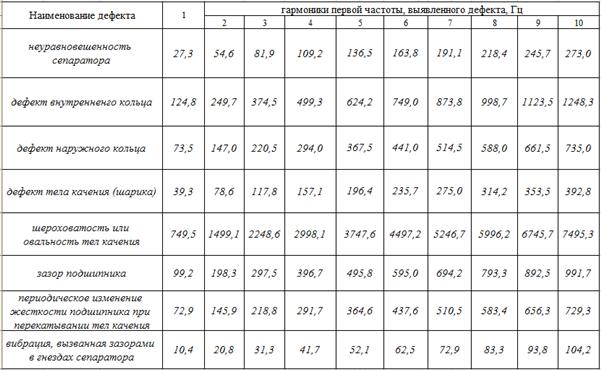
В табл. 3 представлен расчет частот (и гармоник) возможных дефектов шарикоподшипникового узла на угловой скорости вращения 28,3 с-1, так как именно на этом значении угловой скорости вращения УДМ частота анализатора 29,69 Гц имеет наибольшее значение по виброскорости (0,38 мм/с).
При сравнении выявленной частоты с частотами табл. 3 замечено, что частота 29,69 Гц совпадает с расчетной частотой неуравновешенности сепаратора (27,3 Гц) в пределах 8 %. Следовательно, причиной возникновения резонанса в диапазоне угловых скоростей вращения УДМ 26,6 - 45 с-1 является дефект шарикоподшипникового узла - неуравновешенность сепаратора.
Максимальный уровень вибрации шарикоподшипникового узла при выявленном дефекте составляет 77,6 дБ (0,38 мм/с), что на 12,6 дБ больше уровня, предъявляемого к используемому подшипнику.
При анализе виброактивного спектра второго резонанса в диапазоне угловой скорости вращения 70 - 100 с-1 выявлено, что причиной резонанса является недостаточная жесткость конструкции маховика УДМ, первая собственная частота которого меньше номинального значения угловой скорости вращения УДМ.
Табл. 3
Вывод:
Разработанный способ частотного анализа шарикоподшипникового узла позволяет выявлять причину резонанса в области низких угловых скоростей вращения УДМ, а также посредством разработанного программного модуля проводить оценку развития дефектов шарикоподшипников в процессе функционирования УДМ.
Рецензенты:
Гольдштейн А. Е., д.т.н., профессор, заведующий кафедрой информационной измерительной техники Национального исследовательского Томского политехнического университета, г. Томск.
Скрипняк В. А., д.т.н., профессор, заведующий кафедрой механики деформированного твердого тела Национального исследовательского Томского государственного университета, г. Томск.