Анализ фактических режимов ЭС показывает, что выбор указанных параметров вручную без оптимизации даже опытными и квалифицированными сотрудниками диспетчерских служб очень часто приводит к отступлениям от условий допустимости, которых можно было бы избежать, и почти всегда к существенному ухудшению экономичности. Поэтому оптимальный выбор параметров ЭС является актуальным.
Оптимальное управление нормальными режимами ЭС состоит в том, чтобы обеспечить надежное снабжение потребителей электроэнергией требуемого качества при минимальных затратах.
Основным критерием при эксплуатации электрических станций является себестоимость отпущенной потребителям электроэнергии, главной составляющей которой являются затраты на топливо, поэтому оптимальным считается режим, обеспечивающий наименьший расход условного топлива или наименьшие затраты на топливо [3].
Сегодня известно огромное количество методов оптимизации для различных задач, возникающих в энергетике, экономике, логистике и т.д. Причем некоторые методы являются эффективными только для конкретной задачи и абсолютно непригодными для других. Как правило, наиболее мощные оптимизационные методы требуют недопустимо больших затрат машинного времени для больших задач, соответствующих сетям энергосистем. С другой стороны, более быстрые методы обычно менее надежно сходятся и (или) для них нужны ограничительные формулировки задачи и допущения при моделировании. Ни один из используемых на практике методов не гарантирует получение решения задачи, имеющей допустимые решения, и не гарантирует определение глобального оптимума. На сегодняшний день трудно сказать, будет ли разработан один-единственный метод, который бы обладал необходимым быстродействием, надежностью и гибкостью для решения всех оперативных задач [8].
Традиционные методы оптимизации имеют ряд ограничений: требование дифференцируемости и монотонности целевой функции, необходимость хорошего начального приближения для нахождения глобального минимума целевой функции, требование неудовлетворительных затрат машинного времени. Наличие этой совокупности недостатков обусловливает применение и исследование новых нетрадиционных методов оптимизации, которые свободны от указанных недостатков.
В настоящее время рассматриваются вопросы решения технических задач с помощью методов искусственного интеллекта: нечеткой логики, искусственных нейронных сетей, эволюционных алгоритмов.
Генетические алгоритмы - поисковые алгоритмы стохастической оптимизации, основанные на механизмах генетики (генетического наследования и естественного отбора) [4], [5], в которых сохраняется в упрощенном виде биологическая терминология. Основные определения: хромосома - вектор из нулей и единиц (исследуемый объект); гены - позиции вектора (свойства объекта); индивидуум (генетический код) - набор хромосом (вариант решения задачи); кроссовер - операция, при которой две хромосомы обмениваются своими частями; мутация - случайное изменение одной или нескольких позиций в хромосоме.
До начала моделирования эволюционного процесса необходимо создать случайную популяцию - несколько индивидуумов со случайным набором хромосом (числовых векторов). Генетический алгоритм имитирует эволюцию популяции как циклический процесс скрещивания индивидуумов и смены поколений. Жизненный цикл популяции представляет собой несколько случайных скрещиваний (посредством кроссовера) и мутаций, в результате которых к популяции добавляется некоторое количество новых индивидуумов. Отбор в генетическом алгоритме - процесс формирования новой популяции из старой, в результате которого старая популяция погибает. После отбора к новой популяции опять применяются операции кроссовера и мутации, затем опять происходит отбор и т. д.
Отбор в генетическом алгоритме тесно связан с принципами естественного отбора. Популяция следующего поколения формируется в соответствии с целевой функцией. Чем более приспособлен индивидуум, тем больше вероятность его участия в скрещивании, т. е. размножении.
Таким образом, модель отбора определяет, каким образом следует строить популяцию следующего поколения. Как правило, вероятность участия индивидуума в скрещивании берется пропорциональной его приспособленности. Каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность индивидуумов перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации принимают наилучшего из найденных индивидуумов.
Генетический алгоритм представляет собой комбинированный метод, в котором сочетаются две группы методов оптимизации: переборные и итерационные. Механизмы скрещивания и мутации соответствуют переборной части метода, а отбор лучших решений - градиентному спуску, что обеспечивает высокую эффективность генетического поиска для решения задач оптимизации.
Генетические алгоритмы обладают рядом преимуществ:
- не требуют никакой информации о поведении функции (например, дифференцируемости и непрерывности);
- относительно стойки к попаданию в локальные оптимумы;
- пригодны для решения крупномасштабных проблем оптимизации;
- просты в реализации.
Задача оптимального распределения мощностей в ЭС формулируется математически как стандартная задача оптимизации с ограничениями [2]:
минимизировать f (u, x), (1)
при условии g (u, x) = 0, (2)
h (u, x) ≥ 0, (3)
где u - множество независимых переменных в системе, х - множество зависимых переменных, f (u,x) - некоторая функция цели, например, затраты на выработку электрической энергии. С точки зрения расчета установившегося режима к независимым переменным относятся те, для которых имеется конкретная информация, а именно: мощности узлов, а также модули напряжений генераторов, оснащенных системой автоматических регуляторов возбуждения. Комплексы напряжений относятся к зависимым переменным, которые находятся из решения (2). Равенства (2) представляют собой уравнения установившегося режима (УУР), следующего вида [1]:
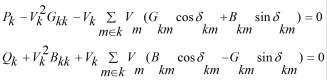 (4)
(4)
где ![]() модуль и фазовый угол комплекса напряжения, активная и реактивная мощности узла k ;
модуль и фазовый угол комплекса напряжения, активная и реактивная мощности узла k ; ![]() - элемент матрицы комплекса узловых проводимостей;
- элемент матрицы комплекса узловых проводимостей; ![]() - разность фазовых углов между смежными узлами k и m.
- разность фазовых углов между смежными узлами k и m.
Неравенства (3) представляют собой предельные ограничения на независимые переменные u и другие режимные ограничения в энергосистеме.
Рассмотрим задачу оптимального распределения мощностей, когда в энергосистеме имеются только тепловые электростанции (ТЭС), на примере стандартной 30-узловой схемы (рис.1) IEEE (Institute of Electric and Electronic Engineers). В данной энергосистеме имеется 6 ТЭС (узлы 1, 2, 5, 8, 11, 13) и 24 нагрузочных станции [9].
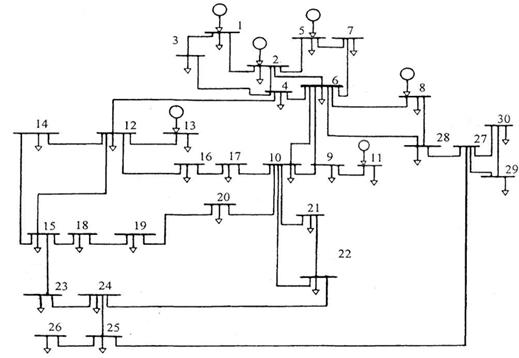
Рис.1
Для агрегатов каждой ТЭС известны расходные характеристики рис. 2, рис. 3 (зависимости стоимости расхода топлива С от активной мощности PГ, вырабатываемой ТЭС). Каждая ТЭС имеет по величине генерирования активной мощности пределы снизу и сверху. Издержки на топливо для каждой ТЭС (зависимость стоимости выработки ($/ч) от генерируемой активной мощности) определяются как
![]() , (5)
, (5)
где а, b, с - известные коэффициенты для каждой станции [8].
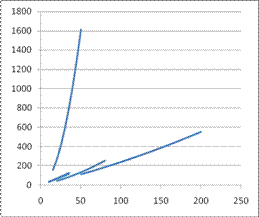
Рис.2
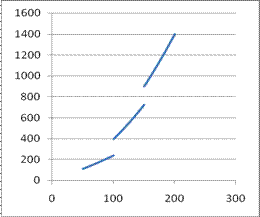
Рис.3
Расчет оптимального распределения мощностей производился для упрощенных расходных характеристик, имеющих вид слабовыпуклых вниз кривых (рис.2), и характеристик, более отвечающих реальным условиям, представляющих собой кусочно-квадратичный полином, общий вид которых изображен на рис.3.
Основные шаги для расчета оптимального распределения мощностей с помощью генетического алгоритма представлены на упрощенной блок-схеме (рис.4):
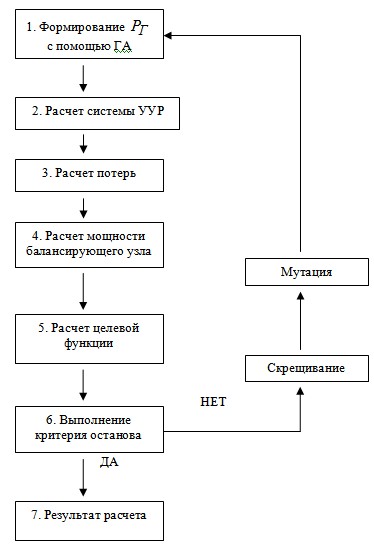
Рис.4
На первом шаге алгоритма с помощью генетического алгоритма формируются значения активной мощности для генераторных узлов 2,5,8,11,13; узел 1 - балансирующий.
На втором шаге расчет системы нелинейных уравнений установившегося режима (4) производится с помощью метода Ньютона.
Расчет суммарных активных потерь (шаг 3):
![]() . (6)
. (6)
Расчет активной мощности балансирующего узла (шаг 4) выполняется по первому уравнению из (4).
Целевой функцией являются минимальные суммарные издержки на топливо для всех ТЭС в системе (5).
Расчет выполняется пока число поколений, заданное для генетического алгоритма, не достигнет своего значения. В противном случае к индивидууму повторно применяются операции скрещивания и мутации.
В конце расчета (шаг 7) будет выбран режим, для которого значение целевой функции имеет наилучшее значение, и параметры которого удовлетворяют заданным требованиям.
Расчет оптимального распределения мощностей 30-ти узловой схемы для упрощенных расходных характеристик (рис.2), выполненный традиционными методами, приведен в [7]. Сравнительные результаты расчетов представлены в табл. 1.
Таблица 1
|
|
Метод расчета |
||
|
Ньютон - Рафсон |
Ньютон |
ГА |
|
|
P1,МВт, |
99,211 |
170,237 |
176,350 |
|
P2,МВт |
80,000 |
44,947 |
48,718 |
|
P5,МВт |
50,000 |
28,903 |
21,466 |
|
P8,МВт |
20,000 |
17,474 |
22,276 |
|
P11,МВт |
20,000 |
12,174 |
12,237 |
|
P13,МВт |
20,000 |
18,468 |
12,000 |
|
Потери, МВт |
5,812 |
8,805 |
9,648 |
|
Стоимость, $/ч |
901,918 |
807,782 |
802,973 |
Сравнительные результаты расчетов с использованием упрощенных расходных характеристик (рис. 2) и характеристик с разрывами (рис. 3) представлены в табл. 2 (номер расчета 1 и 2 соответственно).
Кроме того, в табл. 2 приведены результаты расчета режима системы оптимального по суммарным потерям активной мощности (6) (номер расчета 3).
Таблица 2
|
Номер расчета |
Мощности ТЭС, МВт |
Потери, МВт |
Стоимость, $/ч |
|||||
|
P1 |
P2 |
P5 |
P8 |
P11 |
P13 |
|||
|
1 |
176,35 |
48,71 |
21,46 |
22,27 |
12,23 |
12,00 |
9,64 |
802,97 |
|
2 |
149,93 |
51,48 |
29,95 |
19,98 |
19,94 |
19,82 |
7,73 |
756,47 |
|
3 |
52,01 |
80,00 |
50,00 |
35,00 |
30,00 |
40,00 |
3,61 |
968,88 |
В результате проведенных исследований можно сделать следующие выводы.
1. Использование генетических алгоритмов при оптимизации режима ЭС позволяет, в отличие от традиционных методов, учитывать параметры реальных расходных характеристик электростанций, имеющих разрывы 1 рода, что обеспечивает повышение точности расчета.
2. Применение генетических алгоритмов и учет реальных характеристик обеспечивают уменьшение затрат на топливо на 16 % по сравнению с методом Ньютона - Рафсона и на 6,4 % по сравнению с методом Ньютона.
3. В результате оптимизации режима по суммарным потерям активной мощности в системе удалось снизить потери более чем в два раза. Затраты на топливо в этом случае увеличиваются на 22 %.
Работа выполнена при финансовой поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг., в рамках госконтракта № 539 от 17.05.2010.
Рецензенты:
Шестаков Вячеслав Михайлович, доктор технических наук, профессор, профессор, ПИМаш,г. Санкт-Петербург.
Соловьева Елена Борисовна, доктор технических наук, профессор, профессор, СПбГЭТУ, Санкт-Петербург.
Кирьянов Борис Фёдорович, д.т.н., профессор, профессор кафедры прикладной математики и информатики, Новгородский государственный университет им. Ярослава Мудрого, г. Великий Новгород.



