Моделирование процесса управления организационными системами является сложной научной задачей. В настоящее время для организационных систем разработаны либо вербальные модели выработки управляющих воздействий, либо математические модели, построенные на основе методов теории принятия решений и осуществляющие выбор формализованных альтернатив [1, 3, 6]. При этом в созданных на основе этих моделей системах поддержки и принятия решения (СППР), в основном вырабатывающих только предложения, по-прежнему существенная роль отводится лицу, принимающему решения (ЛПР), что требует для их практического применения наличия подготовленных специалистов. Это вызвано тем, что задача управления организационными системами относится к классу многопараметрических и слабоформализуемых задач, что затрудняет возможность формального получения оптимальных решений. При этом наибольшая сложность заключается в формализованном описании как самих процессов, протекающих в этих системах, так и управляющих воздействий, необходимых для управления объектами системы. Сложность в формализации не позволяет применять в организационных системах стандартные технологии математического моделирования ее процессов и, тем самым, создавать базы моделей для автоматизированных СППР, позволяющих вырабатывать эффективные управляющие воздействии в любых условиях обстановки при минимальном участии ЛПР.
В то же время анализ научных подходов к решению таких задач показал, что возможно эффективное ее решение на основе системного подхода, позволяющего перенести методы описания процессов в технических системах на процессы в системах другого характера.
Постановка задачи
Рассмотрим управление организационной системой как процесс целенаправленного изменения ее параметров, структуры или свойств на основании анализа информации ее состояния с целью достижения оптимального функционирования (достижения интегрального показателя качества) при изменяющихся условиях. В этом случае процесс управления можно представить как замкнутый информационный контур (см. рис. 1), содержащий объект управления, подсистему контроля (идентификации), подсистему выработки и осуществления управляющего воздействия.
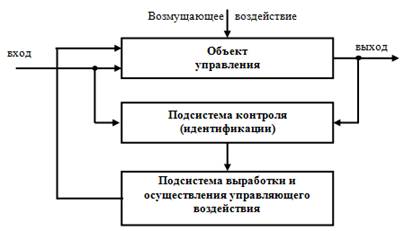
Рисунок 1. Замкнутый информационный контур управления организационной системой
Анализ контура управления, представленного на рис. 1, показывает, что для выработки управляющего воздействия необходимо осуществлять распознавание характеристик объекта управления с учетом приложенных возмущающих воздействий, вызванных изменением его внутренней и внешней среды. В процессе идентификации должны определяться значения функции отклонения результатов деятельности объекта от эталонных требований, после чего осуществляется оценка качества работы управляемого объекта. На основании полученной оценки вырабатывается оптимальная стратегия управления с целью достижения экстремума показателя качества. При таком подходе выработка управляющего воздействия будет заключаться в изменении структуры или параметров объекта управления в сторону оптимального, в соответствии с определенной стратегией. Из приведенного анализа следует, что управление организационной системой представляет собой адаптивный процесс.
Математическое моделирование
Для математического моделирования процесса управляющего воздействия, прежде всего, необходимо осуществить формальное описание структуры объекта и его параметров (признаков). При разработке математических систем наиболее сложным является выбор системы исходных данных, то есть параметров и переменных, описывающих исследуемые объекты, поскольку эти величины должны быть измеримы. Иначе количественный анализ не может быть осуществим.
В настоящее время в рамках теории принятия решения разработаны методы оценивания параметров объектов управления организационных систем. К этим методам относятся методы классификаций, ранжирования, предпочтений, балльного (экспертного) оценивания и ряд других [1, 2, 4]. Однако присущие этим методам классификационные и порядковые шкалы измерения относятся к качественным шкалам и не допускают применения большинства математических операций, что затрудняет их применение для математического моделирования. Кроме того, современные объекты управления достигли такого уровня сложности, что во многих случаях принятие обоснованных управленческих решений и их осуществление становится невозможным без количественного анализа параметров. В свою очередь количественный анализ предполагает использование адекватных математических моделей достаточно высокого уровня сложности. Таким образом, параметры управляемых объектов и осуществляемое на них управляющее воздействие необходимо оценивать количественно.
Для формального задания количественной шкалы воспользуемся эмпирической системой [1, 3, 4] с заданным отношением:
![]() , (1)
, (1)
где ![]() - множество элементов (характеристик, признаков) объекта,
- множество элементов (характеристик, признаков) объекта, ![]() - множество соотношений между элементами и их характеристиками.
- множество соотношений между элементами и их характеристиками.
С целью упрощения анализа произвольных организационных систем в работе [1] предлагается рассматривать универсальную систему с числовыми отношениями:
![]() , (2)
, (2)
где Cэ - множество действительных чисел, Cy - множество отношений между числами.
В связи с тем, что система (2) является гомеоморфной к системе (1), задачу измерения можно сформулировать следующим образом: «Дано (1), найти (2)». Для решения этой задачи введем понятие количественной шкалы как совокупности эмпирической системы Sэ, числовой системы Sy и отображения Ψ, называемого измерением, такого, что соотношение ![]() между элементами Р имеет место тогда и только тогда, когда имеет место отношение
между элементами Р имеет место тогда и только тогда, когда имеет место отношение ![]() между числами, отображающими элементы Р на числовой оси. В этом случае количественное значение Х измеряемого параметра будет представлять собой функционал вида
между числами, отображающими элементы Р на числовой оси. В этом случае количественное значение Х измеряемого параметра будет представлять собой функционал вида
![]() . (3)
. (3)
Возможно существование нескольких шкал k с разными отображениями Ψk, взаимосвязанными между собой функциями преобразования. С учетом изложенного процедуру измерения параметров для объектов организационных систем можно трактовать как определение числовых значений, объективно оценивающих изменения этих объектов.
Системный анализ объектов управления организационных систем позволил установить, что к наиболее объективным количественным шкалам измерения параметров этих объектов относятся время Т и величина ресурсов R, необходимых для реализации целевой установки. Действительно, для выполнения любой задачи организационной системе необходимы, с одной стороны, ресурсы, а с другой стороны - время. Следовательно, количественные изменения Х, происходящие в управляемых объектах организационной системы, можно описать и измерить в виде изменений времени ΔT и количества затраченных ресурсов ΔR, в том числе и энергетических ресурсов, затраченных персоналом на выполнение этих изменений. Адекватность данного утверждения подтверждается тем, что любое управляющее воздействие на объект управления организационной системы можно представить в виде совокупности количества всех видов ресурсов, необходимых для решения этой задачи, и минимального времени, необходимого для достижения целевой деятельности.
Измерение времени, необходимого для управляющего воздействия и выполнения задач, не вызывает затруднения, поэтому остановимся на измерении количества ресурсов. Решение этой задачи предлагается осуществлять методом функционально-стоимостного анализа [4, 5], который позволяет определить затраты на все функции управления и операции, выполняемые системой, в виде стоимостного эквивалента. Таким образом, количественное значение Х формализованного параметра в исследуемом объекте представляет собой функциональную зависимость от двух координат, а именно: от стоимости ресурсов CR и от времени T.
На основании практики управленческой деятельности в организационных системах сделаем допущение, заключающееся в том, что пара числовых элементов CR и T принадлежит гильбертовому пространству H, образованному ортогональными вектор-функциями ![]() и
и ![]() и имеющему норму
и имеющему норму ![]() . Тогда функционал вида (3) представляет собой линейный ограниченный функционал, равный скалярному произведению фиксированного элемента
. Тогда функционал вида (3) представляет собой линейный ограниченный функционал, равный скалярному произведению фиксированного элемента ![]() на текущий элемент
на текущий элемент ![]() , то есть
, то есть
![]() , (4)
, (4)
Ограниченность данного функционала определяется тем, что он не определен в нулевых значениях CR и T. Действительно, в том случае, когда время T или количество ресурсов CR равны нулю, тогда невозможно выполнить задачу, а управляющее воздействие, имеющее такие численные параметры, в свою очередь, будет не реализуемым.
Для того чтобы данный количественный параметр X можно было использовать в математических моделях, описывающих процессы организационного управления, он должен обеспечивать удобство вычислений. Поскольку наиболее простым представлением таких математических моделей является матричное представление, то для обеспечения удобства вычислений параметр X представим его в виде комплексного числа, причем одна его координата, например, стоимость ресурсов CR, будет представлять реальное значение, а другая координата, например, время T, мнимое значение, или наоборот. Это позволит легко вычислять требуемое управляющее воздействие с помощью известных матричных преобразований.
Итак, после того, как определен и формализован количественно параметр, описывающий управляемые объекты организационной системы, можно непосредственно приступать к моделированию процесса выработки управляющего воздействия. С этой целью проведем исследование структуры объекта управления и взаимодействия его параметров с внутренней и внешней средой системы. В качестве метода исследования выберем методы функционального, факторного и корреляционного анализа организационных систем [1, 5, 6].
Структурно процесс деятельности большинства организационных систем можно представить в виде совокупности параллельных объектов, осуществляющих весовую обработку входящих факторов (параметров) с помощью управляющих воздействий, формируемых субъектом управления. Следовательно, этот процесс можно описать математической моделью на основе линейных алгебраических уравнений.
Пусть имеется n объектов (например, типовых задач деятельности), каждый из которых определяется набором из m признаков (факторов), причем, как правило, m>n. Обозначим через xij значение j-го признака (параметра) для i-го объекта, тогда исходная информация может быть представлена в виде таблицы (см. табл. 1), которую называют матрицей данных. Эта таблица имеет n строк (по числу объектов) и m столбцов (по числу признаков). Каждая строка таблицы соответствует одному из объектов, а каждый столбец - одному из признаков или параметров.
Таблица 1. Матрица данных (взаимосвязанных факторов)
|
Номер объекта |
Номер фактора |
|||
|
1 |
2 |
... |
m |
|
|
1 |
X11 |
X12 |
... |
X1,m |
|
2 |
X21 |
X22 |
... |
X2,m |
|
... |
... |
... |
... |
... |
|
n |
Xn,1 |
Xn,2 |
... |
Xn,m |
Если все m признаков, описываются количественными параметрами X1, ..., Xm, то матрицу данных можно обрабатывать с помощью методов факторного и корреляционного анализа. При этом первый этап обработки связан с вычислением матрицы парных коэффициентов корреляции, которая служит отправной точкой всех методов факторного анализа.
Проведенный анализ показал, что за основу математической модели процесса деятельности организационной системы следует выбрать центроидный метод факторного анализа [7]. Этот метод позволяет представить параметры каждого объекта ![]() в виде совокупности некоторого числа общих наиболее важных факторов F1, F2,..., Fk и ряда характерных мешающих факторов Uj, которые также можно назвать помеховыми факторами. При этом считается, что каждый наиболее важный фактор имеет существенное значение для анализа всех параметров, то есть фактор Fj - общий для всех P1, P2,..., Pm. В то же время изменения в характерном мешающем факторе Uj воздействуют на значения только соответствующего параметра P. Таким образом, характерный мешающий фактор Uj отражает ту специфику параметра Pj, которая не может быть выражена через общие факторы. Исходя из предположения о линейности связи параметров объектов с влияющими на них факторами, запишем
в виде совокупности некоторого числа общих наиболее важных факторов F1, F2,..., Fk и ряда характерных мешающих факторов Uj, которые также можно назвать помеховыми факторами. При этом считается, что каждый наиболее важный фактор имеет существенное значение для анализа всех параметров, то есть фактор Fj - общий для всех P1, P2,..., Pm. В то же время изменения в характерном мешающем факторе Uj воздействуют на значения только соответствующего параметра P. Таким образом, характерный мешающий фактор Uj отражает ту специфику параметра Pj, которая не может быть выражена через общие факторы. Исходя из предположения о линейности связи параметров объектов с влияющими на них факторами, запишем
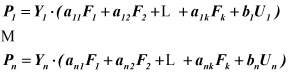 , (5)
, (5)
где ![]() - параметр управляющего воздействия; числа
- параметр управляющего воздействия; числа ![]() - факторные нагрузки, а числа
- факторные нагрузки, а числа ![]() оценивают степень влияния характерного мешающего фактора Ui на Xi.
оценивают степень влияния характерного мешающего фактора Ui на Xi.
Общие факторы F1, F2,..., Fk в модели (5) предполагаются независимыми стандартизованными показателями, распределенными по нормальному закону; характерные факторы U1, ..., Um рассматривают как некоррелированные стандартизованные показатели, независящие от общих факторов. Исходные признаки также считаются стандартизованными переменными с нормальным распределением. Методы определения факторных нагрузок широко описаны в современной литературе по факторному анализу и не вызывают затруднений.
Анализ модели, описанной системой уравнений (5), показывает, что она представляет собой систему их n линейных уравнений с n неизвестными значения параметров управляющего воздействия. Для нахождения однозначного и устойчивого решения данной системы уравнений сделаем ряд допущений. Во-первых, значения выходных параметров управляемых объектов известны априори, поскольку они, как правило, устанавливаются (задаются) инструкциями, регламентирующими и нормирующими реализацию задач деятельности системы. Во-вторых, количественное значение характерных мешающих факторов может быть получено путем экспертной обработки (оценки) статистических измерений на практике. В-третьих, решение системы уравнений (5) будем для удобства осуществлять матричным способом.
Итак, подставляя в выражение (5) вектор Pзад заданных значений выходных параметров, с учетом анализа известных работ [5, 6] делаем вывод, что оптимальная весовая обработка совокупности входных факторов будет достигаться в том случае, если вектор Y управляющих воздействий вычисляется по формуле Винера - Хопфа:
![]() , (6)
, (6)
где ![]() - обратная корреляционная матрица факторного влияния, определяемая из матрицы:
- обратная корреляционная матрица факторного влияния, определяемая из матрицы:
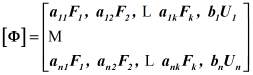 . (7)
. (7)
Выражения (5) - (7) представляют собой не что иное, как математическую модель процесса выработки управляющего воздействия для управляемых объектов организационных систем. При этом управляющее воздействие представляет собой инструкцию, выраженную количественно в виде временного интервала и приращения совокупности ресурсов, необходимых для достижения целевой деятельности организационной системы.
Анализ математической модели показал, что осуществление данного управляющего воздействия приведет к тому, что усилятся влияния наиболее важных факторов F, на достижение заданных конечных результатов процесса целевой деятельности, а влияние характерных мешающих (помеховых) факторов Uj будет частично или полностью компенсировано. При этом если анализ факторов влияния и вычисление управляющего воздействия производить с некоторым временным шагом, то данная математическая модель позволит осуществлять адаптивное управление процессами целевой деятельности.
Выводы
Поставленная в статье научная задача решена, при этом осуществлено формализованное описание параметров управляемых объектов организационных систем и разработана математическая модель процесса выработки управляющих воздействий. Представленная в работе математическая модель имеет большую практическую значимость, поскольку достаточно просто реализуется в реальном масштабе времени на современных средствах вычислительной техники и, следовательно, может быть положена в основу для разработки базы моделей для автоматизированной системы поддержки и принятия решений.
Рецензенты:
Копытов Владимир Вячеславович, доктор технических наук, профессор, начальник управления информатизации, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ставропольский государственный университет», г. Ставрополь.
Будко Павел Александрович, доктор технических наук, профессор кафедры информационных систем и технологий, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ставропольский государственный аграрный университет», г. Ставрополь.



