Устойчивость бортов угольных карьеров определяется комплексом инженерно-геологических факторов, среди которых наибольшее влияние на устойчивость бортов оказывают: геологическое строение и гидрогеологическая обстановка месторождения, прочностные и технологические свойства пород и углей, их трещиноватость, слоистость и раздробленность, а также напряженное состояние самого массива горных пород. Следовательно, учитывая выше приведенные факторы, можно заключить, что для расчета параметров карьера Эльгинского каменноугольного месторождения, при относительно простом его геологическом строении, особо значимым является достоверная оценка физико-механических свойств горных пород и углей в массиве. Прочностные свойства массива горных пород обусловлены двумя основополагающими факторами: прочностью породы в образце и структурно-текстурными особенностями данной толщи горных пород, т.е. ее трещиноватостью и слоистостью.
Для разработки методики определения прочностных параметров горных пород в их естественном залегании (в массиве), по данным геофизических исследований скважин, важное значение приобретает достоверная оценка трещиноватости массива углевмещающих пород. Традиционно трещиноватость горных пород оценивается на обнажениях, в штольнях, по керну и по данным геофизических исследований скважин (ГИС). Использование данных ГИС для определения физико-механических свойств массива горных пород, в данном случае, является наиболее перспективно с точки зрения полноты охвата исследованиями массива по вертикали и возможности равномерного распределения этих исследований по площади месторождения [2].
Изучение интенсивности трещиноватости пород Эльгинского месторождения проводилось на всех стадиях разведки месторождения, в каждой геологоразведочной выработке. Кроме того, была проведена специальная инженерно-геологическая документация пород и углей по скважинам и горным выработкам.
Трещиноватость оценивалась количеством трещин на 1 пог. м. геологоразведочной выработки (коэффициент трещиноватости).
Данные инженерно-геологической документации скважин были использованы для анализа корреляционных связей между коэффициентом трещиноватости (Ктр) и геофизическими параметрами: Jγγi/Jγγоп, dc и ΔТ (где Jγγi -интенсивность рассеянного гамма излучения i-го слоя, Jγγоп - интенсивность рассеянного гамма излучения опорного слоя, которым на Эльгинском месторождении является маркирующий горизонт конгломератов, имеющий минимальное значение Jγγ, dc - приведенный к глубине и нормированный на номинальный диаметр скважины (dc=[ di-0.5ΔH(-0,63) ]/dн), и ΔТ -относительные значения интервального времени распространения продольных акустических волн к их значениям в ненарушенных прочных песчаниках) [4].
В результате проведенного анализа были получены недостаточно тесные корреляционные зависимости с низкими коэффициентами корреляции (R= 0.2 - 0.6), и прогноз Ктр по геофизическим параметрам на основе полученных корреляционных зависимостей нельзя назвать достоверным (рис. 1).
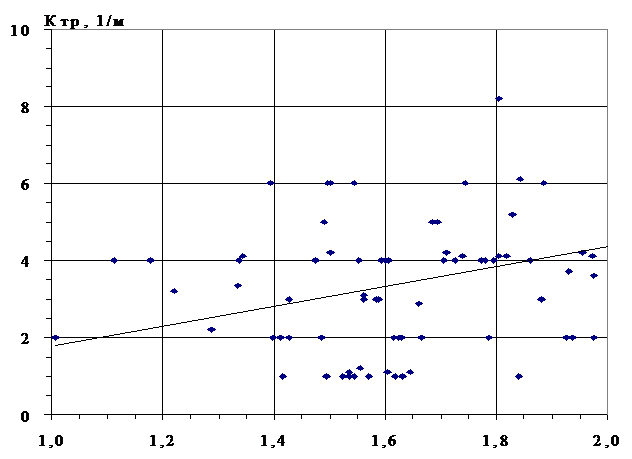
Рис. 1. Сопоставление результатов определения Ктр по инженерно-геологическому описанию керна и геофизическим параметрам
Поэтому нами была использована методика Марковского векторного прогнозирования [1], в основе которой лежит математический аппарат нелинейной Марковской статистики. Марковское векторное прогнозирование позволяет учитывать большое количество факторов (генетических, постгенетических, геологических, геофизических и др.), которые в большей или меньшей степени влияют на достоверность прогноза.
Использование математического аппарата Марковской нелинейной статистики с привлечением имеющейся базы геологических и геофизических параметров, полученных при разведке Эльгинского каменноугольного месторождения, позволило создать математическую модель для расчета Ктр, применительно для данного месторождения.
В основу расчёта параметров модели положен принцип максимального привлечения данных инженерно-геологической документации керна. При этом в качестве основных прогнозирующих факторов при создании модели выбраны: стратиграфическая и современная глубина залегания слоев горных пород; выход керна, регистрируемый при бурении скважин; относительный параметр рассеянного гамма излучения, приведенный к глубине и нормированный на номинальный диаметр скважины. Последовательность включения и место в структуре вектора модели прогноза Ктр, приведенных выше факторов, устанавливалась на основании вариативного подхода и предварительных расчетов наибольшей значимости этих факторов в определении коэффициента трещиноватости массива горных пород [2]. В структуру вектора не включен литологический тип породы по причине слабого контраста горных пород по их физическим свойствам и невозможности литологического расчленения разреза по геофизическим данным, хотя зависимость Ктр от литотипа несомненна.
Структура вектора для прогноза Ктр выглядит следующим образом:
Н - Нстр - ВК - Jγγi/Jγγоп - dc - Jγγi/Jγγоп - ВК - Нстр - Н,
где:
Н - современная глубины залегания слоев горных пород, м;
Нстр - стратиграфическая глубина залегания слоев горных пород;
ВК - выход керна при бурении скважин.
Стратиграфическая глубина вводится в вектор в виде кодов. Коды стратиграфических интервалов обозначают слои горных пород, залегающие между угольными пластами Ундытканской и Нерюнгриканской свит: 1-выше У20, 2- У20-У19, 3- У19-У18, 4-У18-У17, 5- У17-У14, 6- У14-У13, 7- У13-У12, 8- У12-У8, 9- У8-У6н, 10- У6н-У5в, 11- У5в-У4в, 12- У4в-Н16, 13- Н16-Н15, 14- Н15-Н14.
Результаты анализа сходимости коэффициента трещиноватости, определенного по данным геологического опробования и рассчитанного по данным ГИС с использованием Марковского векторного прогнозирования, приведены на рис. 2 и в таблице.
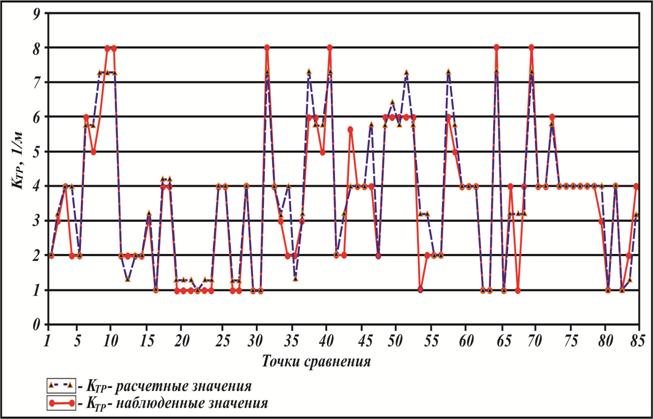
Рис. 2. Сопоставление результатов определения Ктр по методике Марковского векторного прогнозирования и по инженерно-геологическому описанию керна
Таблица
Статистическая оценка математической модели определения коэффициента трещиноватости по геолого-геофизическим данным
|
Статистический параметр |
Средняя систематическая |
Средняя арифметическая |
Средняя квадратическая |
|
Абсолютная погрешность, 1/м |
0,14 |
0,43 |
0,51 |
|
Относительная погрешность, % |
3,86 |
11,90 |
14,06 |
|
Критерий Стьюдента |
1,83 |
|
|
|
Критический критерий Стьюдента |
1,99 |
|
|
Рецензенты:
Ткач Сергей Михайлович, д.т.н., директор, Институт Горного дела Севера им. Н. В. Черского СО РАН, 677980, г. Якутск.
Имаев Валерий Сулейманович, д.г-м.н., профессор, ведущий научный сотрудник лаборатории сейсмологии, Институт земной коры, Сибирское отделение Российской Академии Наук, г. Иркутск.



