Теоретический анализ. Издержки, связанные со старением элемента, накоплением в нем усталостных и износных изменений, его ремонтным обеспечением являются функцией значительного числа переменных.
Во-первых, - это вероятность Q перехода рассматриваемого элемента из работоспособного в неработоспособное состояние к моменту tt в заданных условиях использования.
(1)
где Y(t) - случайная функция, связывающая значение параметра состояния Y с наработкой (временем) t. Предполагается, что вид функции Y(t) априорно известен, так же как и ее основные статистические параметры - математическое ожидание my и дисперсия 
; 
- значение функции Y, соответствует предельному состоянию элемента, характеризующему его отказ.
Во-вторых, экономические характеристики последствий отказа и процессов его предупреждения С.
, (2)
где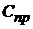 
- потери от простоя машин в связи с отказом элемента;
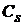- стоимость превентивной замены элемента; 
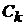- стоимость контроля. На данном этапе исследования стоимость контроля отдельно не учитывается, а включается в состав CS.
Методика. Введем дополнительно характеристику относительной (нормированной) величины издержек при отказе в единицах и долях стоимости превентивной замены элемента.
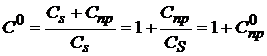(3)
Управление процессом ремонтного обеспечения машины, т.е. управление ее надежностью в эксплуатации характеризуется включением в этот процесс параметров, ответственных за контроль технического состояния, и принятие решений о предупредительной замене (ремонте, регулировке). Издержки, связанные с управлением, зависят как от управляющих параметров, так и от характеристик стохастического процесса старения. К ним можно отнести вероятность нахождения машины в работоспособном состоянии в момент контроля и принятия соответствующего решения:
(4)
где 
- упреждающий допуск на предельное значение контролируемой переменной Y при превентивной замене элемента или в других терминах - допускаемая потеря запаса годности при такой замене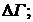 
- наработка между операциями контроля; К1, К2, ...Кn - номер контроля.
В дальнейшем мы будем использовать относительные значения управляющих параметров, а именно:
;
(5)
где m - срок службы элемента в единицах межконтрольной наработки;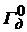
- относительные допускаемое использование запаса годности элемента; 
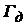- запас годности элемента в момент контроля; 
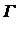- возможный запас годности элемента на начало эксплуатации.
К характеристикам стохастического процесса старения, влияющим на величину издержек, связанных с управлением, можно отнести и экономические характеристики, связанные с превентивно осуществляемой заменой. Вычисление функции (4) сводится в теоретическом плане к решению задач о среднем числе выбросов па и пр случайной функции Y(t) за уровни 
и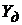 
для промежутка времени 
, являющегося периодически повторяющейся частью общего времени Т использования элемента [1]. В общем виде это решение можно записать следующим образом:
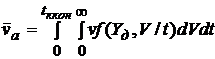, (6)
где V(t) - скорость изменения ординаты случайной функции Y(t) ,
- двухмерный закон распределения ординаты случайной функции Y=
и ее производной в момент t.
Для нормальных стационарных процессов и в случае их независимости от взаимного влияния и 
уравнение (6) решалось бы достаточно просто. Тогда для стационарного процесса можно записать:
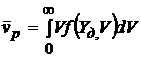. (7)
Для нормального процесса двухмерная плотность распределения вероятности f(Y,V) распадается на произведение нормальных плотностей распределения для 
, можно поэтому написать:
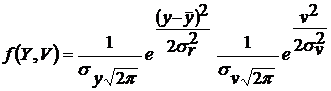. (8)
Подставляя (8) в (7), получим для среднего числа выбросов в единицу времени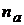 
и 
:
,
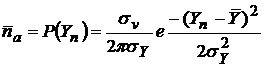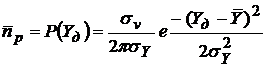(9)
Однако в нашем случае вероятности 
и P(
) зависимы друг от друга, а случайный процесс изменения параметра состояния не всегда подчинен нормальному закону. Кроме того, наличие дополнительного переменного параметра - периодичности контроля, значения которого влияют на вероятность нахождения элемента в исправном или в неисправном состоянии и оптимизация которого входит в круг решаемой задачи, делает аналитическое решение чрезвычайно сложным и едва ли выполнимым делом. К этому добавляются трудности с вычислением па и пр как аналогов временной плотности выбросов случайной функции Y за уровни 
и 
во всем периоде 
использованием функции восстановления. Все это серьезно усложняет математическую модель и расчеты. Поэтому будем подсчитывать издержки за весь период Т в предположении, что замены осуществляются только на новые элементы. Для детали машины это допущение естественно, для машины как элемента в дальнейшем будет снято.
Общее число превентивных замен элементов, не отказавших за период Т, можно выразить интегральным уравнением Вольтерра второго рода, именуемым в теории надежности функцией восстановления [2, 3]:
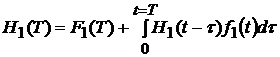, (10)
где Н1(Т) - среднее число превентивных замен за время T; F1(Т) - функция распределения времени до превентивной замены;
;τ - переменная интегрирования.
Соответственно затраты, связанные с превентивными заменами за период Т, запишутся тогда так:
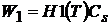. (11)
Аналогично, общее число замен элементов, отказавших за период Т, будет равно:
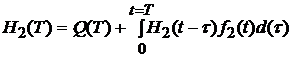(12)
а затраты, связанные с их заменой:
. (13)
Складывая 
и 
и переходя к нормированным и удельным значениям, получим суммарные удельные издержки за период Т в виде:
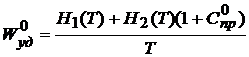. (14)
Сочетание управляющих параметров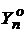 
и 
, при котором величина 
достигает минимума, будем называть оптимальными параметрами управления техническим состоянием элемента в соответствии со стратегией технического обслуживания и ремонта машин «по состоянию», при задаваемых значениях 
и известных характеристиках естественного (неуправляемого) процесса изменения его состояния. Аналитическое решение поставленной задачи, учитывая входящие в ее описание случайные функции и интегральные уравнения, как было уже сказано, едва ли возможно, а на фоне широко распространенной вычислительной техники и нецелесообразно. Продуктивнее использовать численные методы.
Экспериментальная часть. Мы остановились на наиболее естественном для решения таких задач методе статистических испытаний (методе Монте-Карло), позволяющем воспроизводить на имитационной модели случайный процесс появления отказов элементов машины по мере роста наработки и прослеживать последствия их упреждения за счет превентивных замен [4, 5].
Случайная функция состояния Y(t) задается ее математическим ожиданием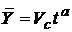 
и плотностью распределения интенсивности (квазискорости) изменения параметра состояния (интенсивности потери годности элемента машины) 
.
Параметрами этой функции являются: среднее значение интенсивности изменения функции состояния 
; коэффициент вариации интенсивности изменения функции состояния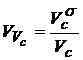 
, значения которого изменяются в интервале 0,2...0,4 через 0,1;
Параметр, а=1 ...2 , шаг изменения которого равен 0,1; наработкой до j-го контроля в i-ой реализации 
.
Рассмотрим:
- событие Ai с параметрами 
, при 
, 
;
- событие 
: 
и 
при 
, .
Наработка до события А или В в i-ou реализации обозначим как tABi.. Задача состоит в отыскании оптимального значения состояния элемента 
, при котором затраты, связанные с превентивными заменами отказавших элементов на единицу рабочего времени, будут минимальными:
,
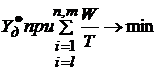где п - число реализаций; т - число межконтрольных периодов.
При моделировании 
параметры задаются в определённом интервале. Аргументы С°р и т варьируются. Определяются:
- число аварийно замененных элементов 
;
- число профилактически замененных элементов 
в расчете на единицу наработки функции в функции 
и 
;
- суммарные удельные издержки 
на единицу наработки в 
и m;
- нормированное оптимальное значение состояние элемента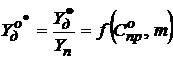 
.
Если А, то 
; если В, то 
; если 
, то 
.
Вывод. Проведенный анализ указывает на необходимость существенной корректировки технической документации на техническое обслуживание и ремонт сельскохозяйственной техники в части допустимых при ремонте размеров и вообще любых параметров состояния, нормативные значения которых были оптимизированы в экономических условиях, существенным образом отличающихся от нынешних.
Рецензенты:
-
Подольский Владислав Петрович, доктор технических наук, профессор, заведующий кафедрой строительства и эксплуатации автомобильных дорог ФГБОУ ВПО «Воронежский государственный архитектурно-строительный университет», г. Воронеж.
-
Устинов Юрий Фёдорович, доктор технических наук, профессор, профессор кафедры инженерной механики и строительной техники ФГБОУ ВПО «Воронежский государственный архитектурно-строительный университет», г. Воронеж.