В работах [1; 2] было показано, что в качестве структурного модуля при структурно-кинематическом синтезе плоских рычажных механизмов можно использовать четырехзвенную исходную кинематическую цепь (ИКЦ). Такой подход к синтезу плоских механизмов позволяет свести задачу их структурно-кинематического синтеза к решению задачи синтеза ИКЦ, что очень удобно для автоматизации проектирования механизмов. В данной работе показано, что указанный подход можно распространить на задачу структурно-кинематического синтеза пространственных рычажных механизмов.
Представлено решение задачи синтеза пространственной ИКЦ со сферическими кинематическими парами и показано ее использование в качестве структурного модуля при структурно-кинематическом синтезе пространственных рычажных механизмов по заданным положениям входного и выходного звеньев. Метод решения задачи синтеза ИКЦ со сферическими парами основан на введении двух подвижных тел, неизменно связанных с входным и выходным звеньями, и в отыскании круговых точек в относительном движении этих тел [3].
Цель исследования: структурно-параметрический синтез пространственных рычажных механизмов.
Материал и методы исследования опираются на основы высшей математики и теории механизмов и машин.
Постановка задачи. Пусть заданы N конечноудаленных положений двух твердых тел ![]() и
и ![]() ,
, ![]() , где
, где ![]() - эйлеровы углы относительно неподвижной системы координат OXYZ систем координат Ax'y'z' и Dx²y²z², неизменно связанных с телами Q1 и Q2 соответственно.
- эйлеровы углы относительно неподвижной системы координат OXYZ систем координат Ax'y'z' и Dx²y²z², неизменно связанных с телами Q1 и Q2 соответственно.
Требуется найти точки ![]() в неподвижной системе координат,
в неподвижной системе координат, ![]() тела Q1 и
тела Q1 и 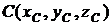 тела Q2 такие, чтобы расстояние между точками В и С во всех положениях тел Q1 и Q2 мало отличалось от некоторой постоянной величины R (рис. 1).
тела Q2 такие, чтобы расстояние между точками В и С во всех положениях тел Q1 и Q2 мало отличалось от некоторой постоянной величины R (рис. 1).
Решение задачи. Введем взвешенную разность для i-го положения тел в виде:
![]() (1)
(1)
Она является функцией десяти параметров: XA, YA, ZA, xB, yB, zB, R, xC, yC, zC. Группируя эти параметры по четыре с общим параметром R, взвешенную разность представим в трех различных формах:
![]() (2)
(2)
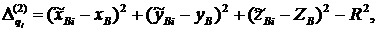 (3)
(3)
![]() (4)
(4)
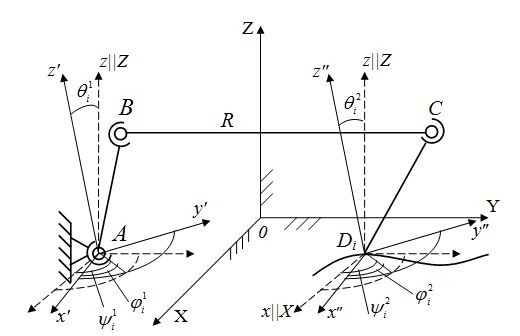
Рисунок 1. Исходная кинематическая цепь со сферическими парами.
здесь:
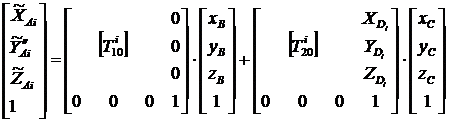 , (2/)
, (2/)
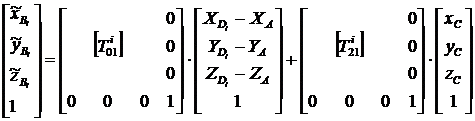 , (3/)
, (3/)
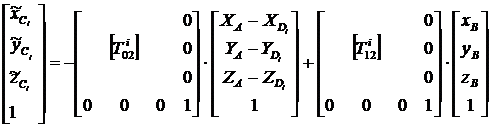 , (4/)
, (4/)
![]() - матрица перехода от k-той системы координат к j-той системе, определяемые как
- матрица перехода от k-той системы координат к j-той системе, определяемые как
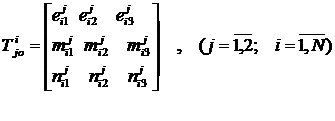 (5)
(5)
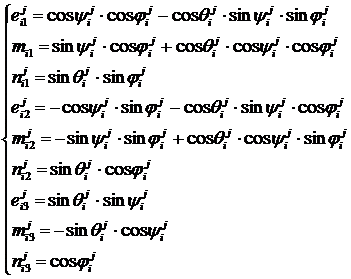 (6)
(6)
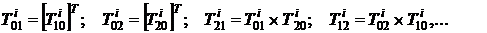 (7)
(7)
Необходимые условия минимума суммы квадратов взвешенной разности:
![]() (8)
(8)
можно записать в виде следующей системы уравнений:
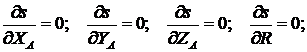 (9)
(9)
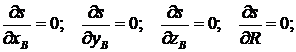 (10)
(10)
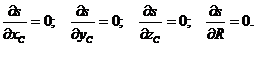 (11)
(11)
Из (9) с учетом (2) и (8) получим:
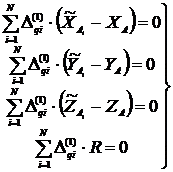 (12)
(12)
Допустим, что 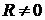 . Тогда из последнего равенства системы (12) следует, что
. Тогда из последнего равенства системы (12) следует, что
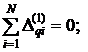 (13)
(13)
С учетом (13) система уравнений (12) принимает вид:
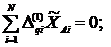
![]()
![]()
![]() (14)
(14)
Подставляя выражения для ![]() из (2) в систему (14), получим:
из (2) в систему (14), получим:
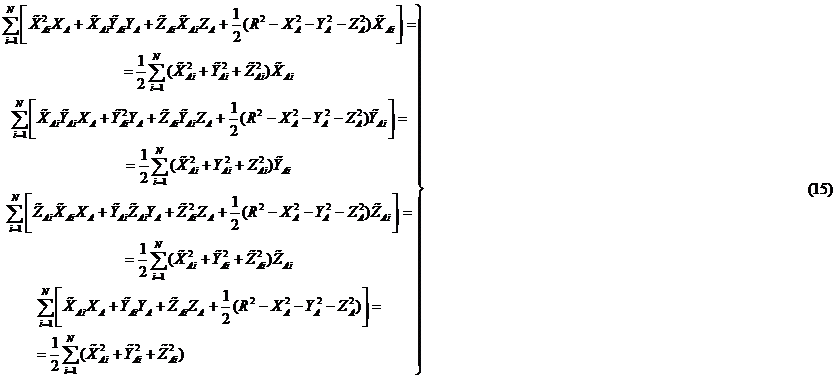
Система (15) линейна относительно переменных ![]() и
и 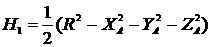 , поэтому ее можно записать в виде:
, поэтому ее можно записать в виде:
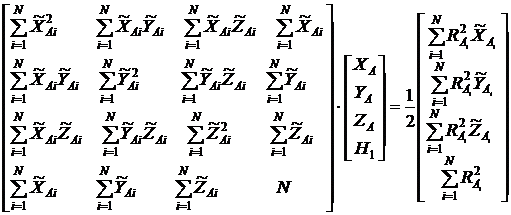 , (16)
, (16)
здесь ![]()
Решение этой системы по правилу Крамера при ![]() имеет вид:
имеет вид:
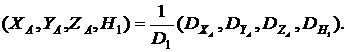 (17)
(17)
Аналогично из (10) с учетом (3) и (8) получим систему линейных уравнений относительно неизвестных ![]() :
:
 (18)
(18)
Решая эту систему по правилу Крамера при ![]() , получим:
, получим:
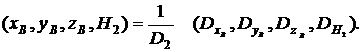 (19)
(19)
Из (11) с учетом (4) и (8) получим систему линейных уравнений относительно неизвестных xC, yC, zC, H3:
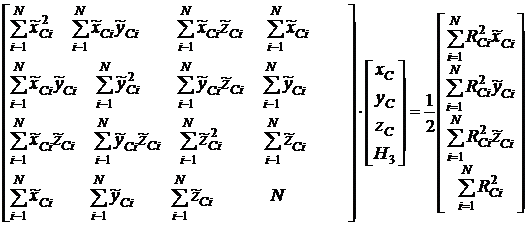 (20)
(20)
Отсюда находим xC, yC, zC, H3 при ![]() :
:
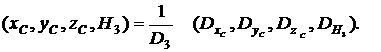 (21)
(21)
Исключая первые четыре неизвестных XA, YA, ZA, R на основе формулы (16), можно свести систему (9)-(11) к системе из шести уравнений с шестью неизвестными ![]() , которую удобно представить в виде:
, которую удобно представить в виде:
 (22)
(22)
Уравнения этой системы по виду совпадают с тремя уравнениями тринадцатой степени относительно трех неизвестных, приведенными в работе [4], хотя в данном случае имеем систему из шести уравнений относительно шести неизвестных. Решение системы (22) представляет трудоемкую задачу, поэтому гораздо эффективнее применять следующий алгоритм поиска минимума функции S:
1. Задаемся произвольно начальными точками ![]()
2. Решаем систему линейных уравнений (16) и определяем ![]()
3. Задаемся точками ![]()
4. Решаем систему уравнений (18) и определяем ![]()
5. Задаемся точками ![]()
6. Решаем систему уравнений (20) и определяем 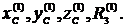
7. Далее циклически повторяем шаги (1-6), заменяя начальные точки В(0) и С(0) на найденные В(1) и С(1).
Применяя алгоритм, получим убывающую последовательность значений целевой функции ![]() имеющую предел, равный значению функции S в точке локального минимума. В результате решения задачи определяются точки
имеющую предел, равный значению функции S в точке локального минимума. В результате решения задачи определяются точки ![]() в неподвижной системе координат
в неподвижной системе координат ![]() , такие, что совмещая с ними звено ВС, получаем искомую ИКЦ в виде разомкнутой цепи ABCD.
, такие, что совмещая с ними звено ВС, получаем искомую ИКЦ в виде разомкнутой цепи ABCD.
Задавая в различных комбинациях часть искомых параметров синтеза, получим различные модификации ИКЦ.
1. Если заданы координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q1 и координаты точки
тела Q1 и координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q2 , то получим трехзвенную незамкнутую цепь ABCD (рис. 2).
тела Q2 , то получим трехзвенную незамкнутую цепь ABCD (рис. 2).
Необходимые условия минимума суммы S в данном случае принимают вид:
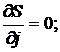 ( j = xB, yB, zB, R, xC, yC, zC);
( j = xB, yB, zB, R, xC, yC, zC);
и для нахождения минимума S можно использовать алгоритм, приведенный выше, учитывая, что параметры ![]() заданы и не требуют определения.
заданы и не требуют определения.
Если точки ![]() и
и ![]() фиксированы, то в результате синтеза ИКЦ получим пространственный четырехзвенник ABCD.
фиксированы, то в результате синтеза ИКЦ получим пространственный четырехзвенник ABCD.
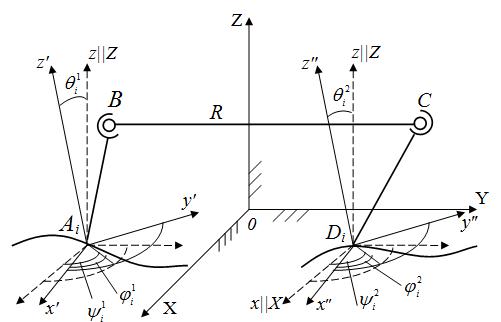
Рисунок 2. Трехзвенная кинематическая цепь.
2. Пусть заданы координаты ![]() точки С
точки С![]() Q2, координаты
Q2, координаты 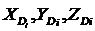 точки D тела Q2 и углы Эйлера
точки D тела Q2 и углы Эйлера ![]() тела Q1, а искомыми параметрами являются
тела Q1, а искомыми параметрами являются ![]()
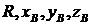 (рис. 3).
(рис. 3).
Необходимые условия минимума сумма S принимают вид:
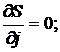 ( j = XA, YA, ZA, R, xB, yB, zB).
( j = XA, YA, ZA, R, xB, yB, zB).
Для нахождения минимума функции S можно опять использовать алгоритм, приведенный выше, учитывая, что ![]()
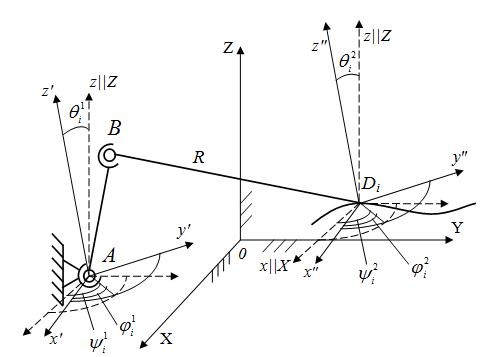
Рисунок 3. Трехзвенная кинематическая цепь.
3. Пусть заданы координаты ![]() = 0 точки В тела Q1 и координаты точки
= 0 точки В тела Q1 и координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q2. Исходная задача сводится к определению сферы наименее удаленной от N положений фиксированной точки С тела Q2.
тела Q2. Исходная задача сводится к определению сферы наименее удаленной от N положений фиксированной точки С тела Q2.
Необходимые условия минимума суммы S:
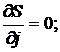 ( j = XA, YA, ZA, R, xC, yC, zC).
( j = XA, YA, ZA, R, xC, yC, zC).
Данная задача подробно исследована в работе [4]. Для ее решения можно применить и алгоритм, приведенный выше, полагая ![]() =0, но в этом частном случае алгоритм поиска минимума полностью совпадает с методом кинематической инверсии.
=0, но в этом частном случае алгоритм поиска минимума полностью совпадает с методом кинематической инверсии.
Результаты исследования и их обсуждение
Результаты исследования приведены конкретными решениями задач синтеза. Решена задача синтеза ИКЦ со сферическими кинематическими парами и их модификации, которые могут быть использованы как модули структурно-кинематического синтеза пространственных рычажных механизмов по заданным положениям входного и выходного звеньев.
Выводы
На основе задания двух подвижных тел проводится кинематический синтез механизмов по заданным положениям входного и выходного звеньев.
Рецензенты
-
Мендебаев Т.М., д.техн.н., профессор, заведующий кафедрой «Стандартизация, сертификация технологии машиностроительного производства», КазНТУ им. К.И. Сатпаева, г. Алматы.
-
Даусеитов Е.Б., д.техн.н., профессор кафедры «Прикладная механика и основы конструирования машин», КазНТУ им. К.И. Сатпаева, г. Алматы.
-
Антонов А.В., д.техн.н., профессор, декан факультета кибернетики, Обнинский институт атомной энергетики Национального исследовательского ядерного университета МИФИ, г. Обнинск.



