Авторами разработан алгоритм построения результирующей онтологии из нескольких исходных на основе результатов сравнения концептов, отношений и атрибутов. Задача интеграции ИС сводится к задаче построения отображений и интеграции онтологий, а затем и установление взаимосвязей схем интегрируемых ИС, т.е. сохранение соответствия множества онтологий ИС заданному набору семантических зависимостей, позволяя установить взаимодействие между ИС.
Как правило, объектная схема ИАИС вуза включает в себя элементы, которые соответствуют сущностям разных предметных областей, каждый объект характеризуется значениями набора атрибутов и представляется как множество упорядоченных пар вида
(1)
где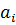 
- атрибут объекта, 
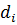- значение атрибута 
, n - количество атрибутов.
Базовым понятием предлагаемой модели является концепт C. Каждый концепт онтологии информационной системы идентифицируется по имени и характеризуется типом. Поэтому концепт зададим как:
, (2)
где 
- уникальное имя (идентификатор) -го концепта; 
- тип i-го концепта (абстрактный, представимый, либо составной).
Зададим следующее множество концептов 
и множество отношений между концептами:
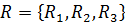, (3)
где 
- отношение наследования (отношения «класс-подкласс»),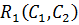 
, где 
- надкласс концепта C2;
R2- отношение агрегации (отношения «часть/ целое»), 
: атрибуты концепта C1 входят во множество атрибутов всех концептов A'.
R3- отношение ассоциации (семантические отношения), обладающее свойством транзитивности.
Вводится функция интерпретации I, сопоставляющей каждому концепту онтологии множество элементов объектной схемы информационной системы, и каждой роли - декартово произведение таких множеств. Интерпретация называется моделью онтологии 
, если она удовлетворяет всем значениям в C и R. Онтология, не имеющая моделей, называется противоречивой.
Описание онтологических моделей информационных систем, автоматизирующих деятельность ВУЗа, которые состоят из информационных объектов, формально можно представить в следующем виде:
, (4)
где 
- множество концептов; 
-множество атрибутов концептов;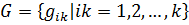 
-множество ограничений, накладываемых на атрибуты;
- отображение, задающее для каждого концепта множество его атрибутов; 
- отображение, задающее ограничения на каждый атрибут; R - множество отношений; I - функция интерпретации.
Информационная система, использующая онтологию O, представлена в виде:
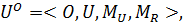(5)
где 
- множество элементов объектной схемы ИС;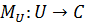 
- отображение, ставящее в соответствие элементу объектной схемы его концепт, 
- отображение, ставящее в соответствие связям между элементами объектной схемы их отношения в онтологии, и для любого элемента 
выполняется условие: множество атрибутов элемента объектной схемы u соответствует атрибутам его концепта, т.е. 
.
Обозначим через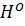 
- множество онтологических моделей информационных систем, использующих онтологию O.
Обозначим изменение информационной системы как отображение:
, (6)
где H0- множество неоднородных информационных систем.
Изменение онтологии:
, (7)
где 
и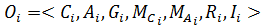 
, и введем обозначения: 
, 
.
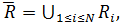
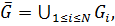
Различные онтологии ИС, входящие в O, могут иметь пересекающиеся множества атрибутов, типов и концептов. На базе нескольких исходных онтологий, которые используют информационные системы, осуществляется построение результирующей онтологии с сохранением исходных спецификаций в таком виде, чтобы она включала все возможные отношения между концептами и не содержала эквивалентные (дублирующие) концепты. Для этого необходимо, чтобы отображения 
на одинаковых концептах онтологий ИС совпадали. Результирующая онтология определяет соответствия концептов и правила их интерпретации между ИС, что позволяет успешно установить их взаимодействие.
Информационная система 
называется интегрированной на множестве ИС 
, если непротиворечиво, т.е. существуют 
, являющиеся расширением соответствующих отображений: 
.
Для осуществления согласованного изменения данных в ИС необходимо установление между онтологиями семантических зависимостей, которые определяют семантическую близость концептов. Таким образом, цель интеграции заключается в сохранении соответствия множества онтологий информационных систем заданному набору семантических зависимостей.
Под семантической зависимостью, заданной на онтологии O, предполагается z-предикат, заданный на 
.
Множество семантических зависимостей 
непротиворечиво, если существует онтология O, которая удовлетворяет зависимости zj.
На практике зависимость между онтологиями необходимо сводить к зависимостям между концептами, которые в них входят. Они были рассмотрены, проанализированы и отнесены в следующие 5 классов:
1. Эквивалентность z1: 
, где b- порог меры семантической близости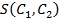 
, при которой строится отображение концепта C1 в онтологию O2.
2. Обобщение ( 
, где 
отображение - отображение, ставящее в соответствие концепту C1 множество концептов C2.
3. Уточнение , где - отображение, ставящее в соответствие множеству концептов C1 концепт C2.
4. Частичная эквивалентность z4.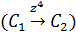 
.
Пересечение множеств атрибутов концептов C2 и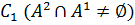 
свидетельствует о наличии общих атрибутов. Это означает, что существует некоторый концепт C, являющийся надклассом для концептов C2 и C1, а сами концепты принадлежат одному уровню иерархии.
5. Различие z5. Пустое пересечение множеств атрибутов концептов C2 и 
.
Модель системы интеграции данных на основе онтологий представим в виде кортежа:
, (8)
где 
- онтология ИС,U0 - информационная система с онтологией O, 
- множество семантических зависимостей, 
такое отображение, что 
, 
, выполнено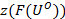 
, 
- отображение онтологий.
Для численной оценки семантической близости концептов онтологий авторами выбран подход, основанный на результатах исследований профессора университета Мангейма (Германия) A. Maedche [4, 5]. В соответствии с этим рассматриваются атрибутивная, таксономическая и реляционная меры, результаты измерений с использованием каждой из них с учетом весовых коэффициентов и используются для комплексной оценки семантической близости.
При этом авторами предлагается определять атрибутивную меру не как пересечение диапазонов числовых значений атрибутов концептов, а как отношение пересечения множеств атрибутов к объединению множеств атрибутов концептов. Предлагается также определять весовые коэффициенты автоматически с использованием генетического алгоритма. Основные преимущества предлагаемого подхода заключаются в выявлении ключевых концептов для построения результирующей онтологии, устранения субъективности описаний понятий онтологии и зависимости от точек зрения разработчиков онтологий.
Определим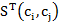 
как мера близости двух концептов на основе их положения,
- мера близости двух концептов на основе сопоставления их отношений,
- мера близости двух концептов на основе сопоставления атрибутов и значений атрибутов концептов.
Мера близости 
двух концептов ci онтологии O и cj онтологии O' определяется как:
, (9)
где t- вес, определяющий важность меры близости 
; r- вес, определяющий важность меры близости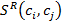 
; α- вес, определяющий важность меры близости 
С учетом того, что 
, 
, причем если концепты идентичны 
, тогда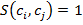 
, если концепты различны и не имеют общих характеристик, тогда 
.
Для автоматического определения параметров 
используется генетический алгоритм, где индивид представляется в виде тройки генов 
. В роли функции приспособленности выступает целевая функция:
.
К сформированной популяции потенциальных решений со следующими ограничениями применяются стандартные операторы отбора, кроссовера и мутации.
Критерий выбора: максимизация суммы мер семантической близости между концептами двух онтологий.
.
Для выделения меры семантической близости, при которой концепты эквивалентны, необходимо выбрать пороговое значение меры близости. Разработан метод определения критерия подобия концептов для классификации отображений в пять групп: эквивалентность, частичная эквивалентность, обобщение, уточнение, неопределенность.
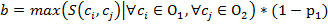, (10)
где p1- процент, при котором b считается порогом подобия для определения эквивалентности концептов.
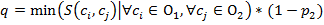, (10)
где p2- процент, при котором считается порогом подобия для определения отсутствия эквивалентности концептов.
Рассмотренная математическая модель реализована на ЭВМ в рамках специального программного обеспечения, использованного при интеграции онтологий, построенных на объектных схемах информационных систем управления учебным процессом и финансового планирования вуза. Обе системы были разработаны независимо друг от друга в период, предшествовавший рассматриваемому исследованию, и функционировали на основе использования собственных локальных баз данных, обмен информацией между которыми осуществлялся с помощью программ-конвертеров.
В результате проведенного вычислительного эксперимента была создана интегрированная онтология, позволившая в короткие сроки объединить локальные базы данных упомянутых систем, исключить дублирование, а также обеспечить целостность и непротиворечивость представленных в них сведений.
Кроме того, аналогичная работа была проведена экспертом-аналитиком, соответствующие результаты представлены в таблице 1.
Таблица 1. Сравнение параметров процесса отображения онтологий
|
Способ интеграции |
Найденные семантические зависимости |
Критерий оценки (средние значения) |
|||||
|
Обобщение |
Уточнение |
Эквивалентность |
Частичная эквивалентность |
|
|
|
|
|
Полнота (R) |
Точность (P) |
Мера (F1 ) |
|||||
|
Эксперт |
7 |
3 |
4 |
14 |
0,86 |
0,82 |
0,86 |
|
Модель |
12 |
3 |
8 |
16 |
0,98 |
0,94 |
0,98 |
Заключение
Построенная математическая модель интеграции онтологий ИС адекватно описывает их семантические особенности. Алгоритм интеграции с использованием онтологий в целом лишен многих недостатков, присущих чисто техническим методам, и предоставляет возможность разработки интегрированных ИС, работающих с информацией на семантическом уровне. Практическое использование рассмотренных методов моделирования позволило в короткие сроки и с высоким качеством объединить локальные базы данных систем управления учебной деятельностью и финансового планирования в процессе развития ИАИС Бийского технологического института.
Рецензенты:
-
Оскорбин Николай Михайлович, д.т.н., профессор, заведующий кафедрой теоретической кибернетики и прикладной математики ФГБОУ ВПО «Алтайский государственный университет».
-
Темербекова Альбина Алексеевна, доктор педагогических наук, профессор кафедры алгебры, геометрии и методики преподавания математики Горно-Алтайского государственного университета, зав. научно-исследовательской лаборатории «Инновационные образовательные технологии» ГАГУ.