Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

При организации и осуществлении мониторинга технического состояния образцов ракетно-космической техники и составных частей объектов наземной космической инфраструктуры возникает необходимость выявления разнообразных дефектов в элементах оборудования.

Под дефектом понимается каждое отдельное несоответствие продукции требованиям нормативно-технической документации [ГОСТ 17-102].

Постановка задачи исследования

Представим множество вариантов решений по формированию рационального состава комплекса средств технического диагностирования отдельно взятого элемента наземного технологического оборудования ракетно-космического комплекса в виде некоторого конечного множества альтернатив:

 A_{n} = {a₁, ..., a_n}.  (1)

Сравнительную предпочтительность альтернатив будем оценивать с помощью частных показателей K₁, ..., K_s, s > 1. Тогда s-мерная оценка каждой альтернативы a_i, i Î {1, ..., n} может быть представлена вектором:

 X_i<s> = (x_i1, ..., x_is).   (2)

При сравнении альтернатив могут возникать следующие ситуации:

1) альтернатива a_i не менее предпочтительна, чем альтернатива a_j (a_i ≥ a_j), если X_i<s> ≥ X_j<s>, т.е. x_iv ≥ x_jv, v  {1, ..., s};

2) альтернатива a_i более предпочтительна, чем альтернатива a_j (a_i » a_j), если X_i<s> > X_j<s>, т.е. x_iv ≥ x_jv, и хотя бы для одного v x_iv > x_jv;

3) альтернатива a_i недоминируема, если не существует альтернативы a_j  {a₁, ..., a_n} такой, что a_j » a_i.

Естественно, что наиболее предпочтительная среди альтернатив a₁, ..., a_n относится к числу недоминируемых. Недоминируемые альтернативы образуют так называемое множество Парето [1].

Методы ранжирования недоминируемых альтернатив

При выборе наиболее предпочтительных альтернатив, как правило, недостаточно ограничиться указанием множества Парето, которому может принадлежать слишком много альтернатив. Поэтому необходимо использовать другие дополнительные методы сравнительной оценки альтернатив, связанные с построением на множестве Парето отношения предпочтения. Данные методы можно условно разделить по способу ранжирования на три группы (рис. 1).

Рис. 1. Основные методы ранжирования недоминируемых альтернатив.

Метод лексикографического упорядочения [2] целесообразно использовать, когда частные показатели K₁, ..., K_s, характеризующие альтернативы, таковы, что их относительная важность измерима в порядковых шкалах, причем K₁ существенно важнее всех остальных частных показателей, K₂ - всех остальных, за исключением K₁, и т.д.

В этом случае, если a_i » a_j по K₁, то a_i » a_j независимо от оценок по остальным частным показателям K₂, ..., K_s. Если же оценки альтернатив совпадают по первым r частным показателям и различаются по (r+1)-му частному показателю, то более предпочтительной в этом случае является альтернатива, более предпочтительная по (r+1)-му частному показателю.

Легко заметить, что при лексикографическом упорядочении все альтернативы являются строго проранжированными. Одинаково предпочтительными могут оказаться лишь альтернативы с совпадающими векторами оценок. В случае лексикографического упорядочения оказывается легко решаемой задача выбора заданного числа наилучших альтернатив. Для этого достаточно выбрать нужное число первых альтернатив в их лексикографическом упорядочении.

Однако далеко не всегда частные показатели оценивания альтернатив K₁, ..., K_s настолько неравноценны, настолько несоизмеримы по важности. Более типична ситуация, когда важность частных показателей является сопоставимой. В этом случае целесообразно применить различные методы свёртки - построения обобщённого критерия либо, если обобщённый критерий нельзя построить, методы упорядочения без обобщённого критерия.

Методы упорядочения с обобщённым критерием [3] отличаются по способам формирования обобщённого критерия. Наиболее распространены линейные обобщённые критерии, которые строятся в предположении об аддитивности, однородности частных показателей, сопоставимости их по относительной важности и независимости.

Предположение об аддитивности частных показателей означает, что более предпочтительной является альтернатива, у которой выше значение суммы значений частных показателей. В этом случае предполагается, что для лица, принимающего решение, существенным обстоятельством является факт суммарного превосходства альтернативы по всей совокупности рассматриваемых показателей. Однородными считаются показатели, измеряющие интенсивность свойств одной и той же природы. В случае когда показатели таковыми не являются, их необходимо преобразовать в однородные. Сопоставимость по относительной важности для частных показателей означает, что их важность может быть сравнима с использованием количественных шкал (в отличие от порядковых при лексикографическом упорядочении).

Одним из наиболее важных предположений о характере частных показателей при использовании обобщённого критерия является предположение об их независимости.

При соблюдении указанных предположений процедура сравнительной оценки многокритериальных альтернатив сводится к построению обобщённого линейного критерия:

, (3)

где α₁, ..., α_s - есть весовые коэффициенты частных показателей K₁, ..., K_s, отражающие результаты сравнительной оценки частных показателей по важности.

Лучшей признаётся альтернатива a_i, для которой

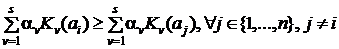  .(4)

Если необходимо выбрать k лучших альтернатив, то ими будут k альтернатив, получивших наибольшие оценки по критерию (3).

Несмотря на достаточную наглядность критерия (3) и простоту его применения на практике, линейный обобщённый критерий не всегда может быть сформирован. В частности, при решении задач выбора вариантов построения комплекса средств ТД некоторые показатели эффективности комплекса являются зависимыми (например, ресурсоемкость в общем случае косвенно зависит от значений показателей результативности и оперативности). Кроме того, не всегда обоснованным представляется применение в этих задачах принципа аддитивности частных показателей.

Отсутствие обобщённого критерия существенно усложняет сравнительную оценку предпочтительности многомерных альтернатив. В этом случае обычно применяются методы упорядочения без обобщённого критерия.

Одним из известных методов из этой группы является так называемый метод ЭЛЕКТРА [4]. В данном методе предлагается определять предпочтения экспертов на множестве многомерных альтернатив, не выясняя структуры и вида обобщённого критерия, а используя дополнительную функцию порогового характера о согласии и несогласии экспертов с результирующим отношением предпочтения альтернатив.

Рассмотрим произвольную пару альтернатив a_i и a_j. Обозначим класс частных показателей, согласно которым a_i не менее предпочтительна, чем a_j, как C (a_i, a_j), а класс, по которому действует обратное предпочтение, как D (a_i, a_j). Пусть известны коэффициенты a_i, ..., a_s, характеризующие относительную важность предпочтений по каждому из частных показателей. В методе ЭЛЕКТРА вводится индекс согласия, характеризующий согласие эксперта с порядком предпочтений a_i » a_j:

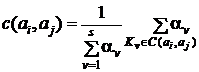 (5)

и индекс несогласия:

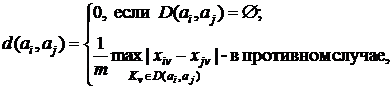  (6)

где m - максимально возможная разность между оценками x_iv и x_jv.

Считается, что альтернатива a_i предпочтительней a_j, только если

 c (a_i, a_j) ≥ c₀ и d (a_i, a_j) ≤ d₀,

где c₀ и d₀ - специально вводимые пороговые значения индексов (5) и (6).

Недостатком данного метода и его модификаций является эвристический характер процедур формирования классов C (a_i, a_j) и D (a_i, a_j), требующий привлечения экспертов для попарного сравнения альтернатив a_i и a_j, недостаточно обоснованный способ задания пороговых значений c₀ и d₀, а также принципиальная возможность получения вариантов упорядочений с нарушением принципа транзитивности при ранжировании альтернатив, т.е. может быть, что

 a_i » a_j, a_j » a_k и a_k »a_i,     (7)

что, конечно, противоречит здравому смыслу при использовании метода в инженерных приложениях.

Решение

Исходя из этого, рассмотрим альтернативный метод выбора наилучшего варианта построения комплекса средств ТД, основанный на решении оптимизационных задач.

Пусть для каждого частного показателя K_v можно указать пороговое значение L_v такое, что альтернативы, оценки которых по показателю K_v ниже, чем L_v, крайне нежелательны. Более предпочтительными считаются альтернативы, оценки которых по частным показателям как можно дальше отстоят от критических значений L_v. Исходя из сущности подхода к ранжированию, данный метод можно назвать методом ранжирования по максимальному удалению от критических значений частных показателей или, сокращённо, методом ранжирования по максимальному удалению (РМУ) [5].

Представим математическую модель, лежащую в основе метода РМУ, в формализованном виде следующим образом.

Пусть альтернативы A = {a₁, ..., a_n} оцениваются по s частным критериям K₁, ..., K_s и X_i<s> = (x_i1, ..., x_is) - вектор оценок альтернативы a_i, i  {1, ..., n}. Альтернативу a_i будем считать более предпочтительной, чем a_j, если

  min{x_i1-L₁, ...,  x_is-L_s} > min{x_j1-L₁, ...,  x_js-L_s}.

Тогда выбор наилучшей альтернативы a* осуществляется как решение задачи

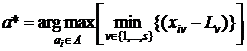.  (8)

Задача (8) может быть решена как задача линейного программирования

 (9)

при ограничениях x_iv - L_v - z_iv  0, v  {1, ..., s}, a_i A.

При небольшом числе альтернатив задача может быть решена непосредственным расчётом значений  и выбором альтернативы с максимальным значением данного критерия.

Обобщим правило (8) на случай, когда частные показатели K_v, v  {1, ..., s} различны по важности. В данной постановке это означает, что удаление оценок альтернатив от критических значений по одним частным показателям важнее, чем по другим. Например, важнее обеспечить более высокие значения показателя результативности по сравнению с показателями ресурсоемкости и оперативности. Или в большей степени можно уступить по показателям результативности целевого применения, зато увеличить показатели оперативности и снизить затраты.

Допустим, что определены значения весовых коэффициентов α₁, ..., α_s, характеризующих важность удаления оценки альтернативы по каждому из частных показателей. Тогда задача (8) может быть записана в виде

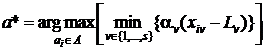 . (10)

Соответственно, задача линейного программирования (9) принимает вид

(11)

при ограничениях x_iv - L_v - z_iv ≥ 0, v  {1, ..., s}, a_i A.

Или, введя функцию 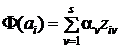, можно записать:

 (12)

 x_iv - L_v - z_iv ≥ 0, v  {1, ..., s}.

Остановимся подробнее на особенностях реализации выбора наиболее предпочтительных вариантов решений по формированию комплекса средств ТД с использованием критерия (10).

Анализ составляющих выражения (10) позволяет выделить следующие аспекты, подлежащие уточнённому исследованию.

1. Формирование полного множества A альтернатив a_i, i = {1, ..., n}.
2. Уточнение основных типов частных показателей K_v, v 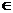 {1, ..., s} и их физической природы.
3. Выбор способа оценивания значений коэффициентов важности частных показателей _v, v 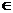 {1, ..., s}.
4. Анализ возможных способов формирования оценок x_iv, i 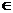{1, ..., n}, v  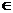{1, ..., s} частных показателей.
5. Исследование способов преобразования частных показателей K_v, v Î {1, ..., s} к однородным.
6. Анализ способов задания критических значений L_v, v 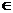 {1, ..., s} частных показателей.
7. Исследование особенностей ранжирования альтернатив по правилу (11) с учётом возможных вариантов сочетания различных типов оценок составляющих данного выражения.

Рецензенты

Смагин Владимир Александрович, д.техн.н., профессор кафедры Военно-космической академии имени А.Ф. Можайского, г. Санкт-Петербург.

Садин Дмитрий Викторович, д.техн.н., профессор, начальник кафедры Военно-космической академии имени А.Ф. Можайского, г. Санкт-Петербург.