Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 0,936

BIOMECHANICS OF SUTURE MATERIALS IN THE ABDOMINAL SURGERY

1

• Authors
• Files
• Abstract
• Keywords
• References

Введение

В последние годы в абдоминальной хирургии, связанной с операциями на органах брюшной полости (рис. 1), всё больше применяются современные рассасывающиеся шовные материалы (нити), которые значительно влияют на благоприятный исход операции [1, 5]. Преимущество шовного материала заключается в прогнозируемых сроках рассасывания. Большую роль также играет способ ушивания раны: различают непрерывный и прерывный (узловой) виды швов. Данные виды ушивания применяются врачами субъективно, т.е. без количественной оценки, с точки зрения биомеханики. Ещё одной проблемой для хирургов является определение оптимального шага шва и силы затяжки для предотвращения образования некрозов в области мягкой ткани. Если врач стягивает нить очень сильно, то в области контакта двух сшиваемых поверхностей блокируются капиллярные сосуды микроциркуляторного русла и развивается некроз ткани [17]. Если сила затягивания будет недостаточной для сопоставления краев раны, то высокий риск возникновения полного выпадения внутренних органов из раны (эвентрация) в раннем послеоперационном периоде и появления вентральных грыж в позднем. Известно, что вентральные (послеоперационные) грыжи возникают в зонах расхождения апоневроза, через которые проникают брюшина и полые органы в подкожно-жировую клетчатку (рис. 2). На рис. 3. представлена статистика локализации грыж [3]. Следует отметить высокий процент послеоперационных грыж, поскольку во время операции хирург не может объективно измерить силу, прикладываемую к нити, и напряжения, возникающие в ткани.

Для объективизации хирургической операции по наложению хирургических швов всё чаще находят применение компьютерные модели, способствующие использованию адекватной техники разрезания раны и её последующего сшивания на основе биомеханических расчётов, а не субъективного опыта, базирующегося в основном на визуальной оценке. Однако следует отметить небольшое количество работ по вычислительной (компьютерной) биомеханике шва [7, 11-16].

 

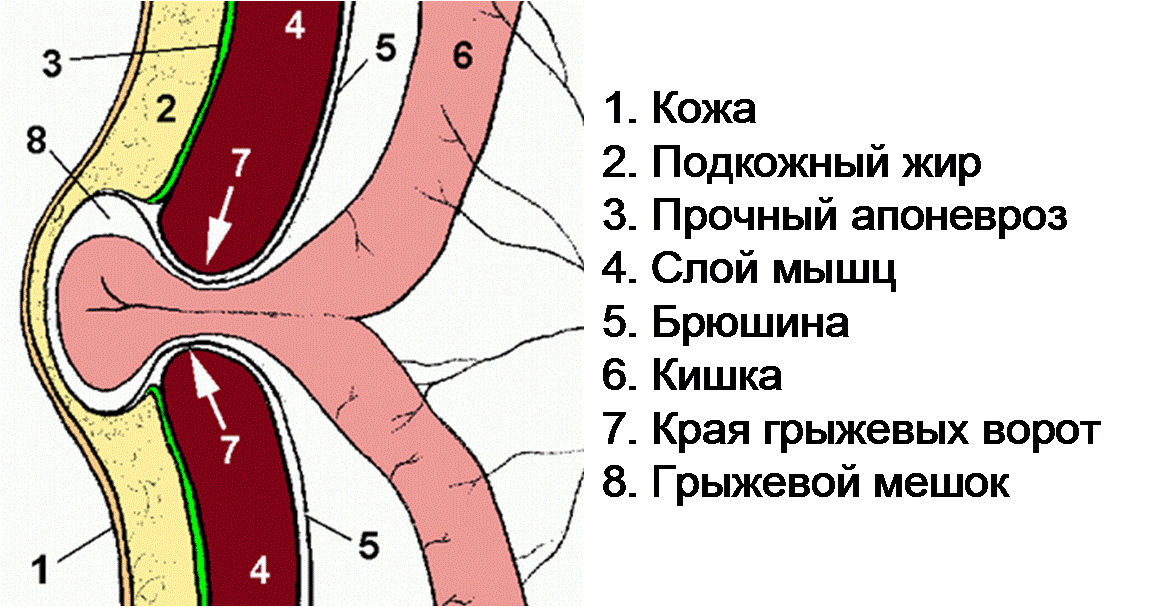
Рис. 1. Анатомическое строение абдоминальной области Рис. 2. Схема грыжи

 

Рис. 3. Статистика образования грыж [3]

Исходя из вышесказанного, целью работы является построение 3D компьютерной модели взаимодействия шовного материала с тканью апоневроза для:

• сравнения способов ушивания тканей (биомеханический анализ сравнения узлового и непрерывного видов швов);
• определения зависимости между силой (F), которая прикладывается к нити при затягивании шва, и напряжениями, возникающими в мягкой ткани апоневроза;
• учёта влияния шага хирургического шва на напряженно-деформированное состояние апоневроза.

Статья состоит из следующих разделов. В разделе 1 приведена оценка механических свойств нитей и апоневроза. Испытания на растяжение-сжатие нитей проводилось в Центре экспериментальной механики Пермского национального исследовательского политехнического университета. Раздел 2 включает в себя постановку задачи взаимодействия нити с тканью апоневроза, а раздел 3 - результаты и их обсуждение. В результате применения методов вычислительной биомеханики получены зависимости σ-F (напряжения в апоневрозе - сила, прикладываемая к нити), σ-d (напряжения в апоневрозе - диаметр нити) и σ-n (напряжения в апоневрозе - количество стежков) для узлового и непрерывного швов.

1. Экспериментальное исследование механических свойств апоневроза и нитей

Экспериментальное исследование механических свойств нитей

Для проведения биомеханического моделирования необходимо знать механические свойства нитей и апоневроза. Механические испытания по одноосному растяжению образцов нитей проводились на установке Instron 5882. Размеры образцов составляли 350 мм в длину, исследованы нити толщиной 3-0, 2-0, 1 по системе USP  как наиболее часто используемые в абдоминальной хирургии. Расстояние между захватами 50 мм, скорость перемещения нижнего захвата 5 мм/мин [4].

Для испытаний медицинского шовного материала проведено исследование следующих типов нитей: «Vicryl», «Vicryl Plus», «Safil», «Atramat», «Polysorb», «PDS Plus», «Monocryl Plus». Для исключения влияния на измерение деформации образца проскальзывания нитей в системе Instron 5882 был использован видеоэкстензометр. Образец в захватах, общий вид машины, а также результаты механических испытаний показаны на рис. 4.

   

а                       б                        в

Рис. 4. Эксперимент по растяжению нитей: а - образец в захватах, б - общий вид машины Instron, в - результаты испытания нитей в исходном состоянии: 1 - «Vicryl+», 2 - «Vicryl»,
3 - «Safil», 4 - «Atramat», 5 - «Polysorb»

 

                                     а                                                                                   б

                                                             

                                      в                                                                                  г

Рис. 5. Виды швов: а - схема узлового шва, б - схема непрерывного шва [2], в - вид хирургической раны при ушивании непрерывным швом, г - ушитая непрерывным швом рана

Экспериментальное исследование механических свойств апоневроза

Данные по исследованию образцов апоневроза были взяты из работ [8, 9], в которых сравнивались механические свойства апоневроза индейки (к сожалению, данных по исследованию апоневроза человека в доступной авторам литературе найдено не было), в продольном и поперечном направлениях. Поверхностные апоневрозы были извлечены из девяти замороженных трупов индюков; пучки мышц, прикреплённые к апоневрозу, были удалены. Перед испытаниями образцы хранились в физиологическом растворе Рингера.

Из экспериментов на растяжение и разрыв было показано, что апоневроз жестче в продольном, чем в поперечном направлении.

2. Постановка и решение задачи о взаимодействии нити с тканью апоневроза

В работе рассматривается взаимодействие апоневроза с современными рассасывающимися материалами (нитями Monocryl, PDS 2, Vicryl, Safil).

Целью работы является:

• сравнение способов ушивания (биомеханический компьютерный анализ сравнения узлового и непрерывного видов швов (рис. 5));
• определение зависимости между силой (F), которая прикладывается к нити при затягивании шва, и напряжениями, возникающими в мягкой ткани апоневроза;
• учёт влияния шага хирургического шва на напряженно-деформированное состояние апоневроза.

Упругие константы нитей и апоневроза, которые брались из полученных экспериментальных данных (см. раздел 1) и из работ [4-6, 8], представлены в табл. 1.

При решении задачи использовались следующие предположения:

1. Апоневроз и нить являются упругими изотропными телами.
2. Апоневроз моделируется как прямоугольная пластина с реальными анатомическими размерами.
3. Поскольку в предварительных расчётах было показано, что на напряженно-деформированное состояние мягкой ткани гораздо большее влияние оказывает внутрибрюшное давление, а не усилия связок, с помощью которых апоневроз крепится к другим анатомическим областям, то в данном случае апоневроз считается жестко закрепленным.
4. Cогласно эффекту Старлинга, нарушение микроциркуляторного кровоснабжения происходит при σ=1 кПа, поэтому именно данный критерий был выбран для анализа напряжений, возникающих в апоневрозе.
5. Задача взаимодействия узлового шва с апоневрозом - осесимметричная.
6. При моделировании узлового шва учитывалось, что в процессе затягивания шва хирург прикладывает к нити постоянную нагрузку F, далее шов завязывается. После этого врач делает последующий стежок. При моделировании этого процесса считалось, что при прекращении воздействия хирурга после завязывания остаточная нагрузка составляет 0,8F.

Расчётная схема задачи показана на рис. 6. Рассматривается некоторый объём ткани апоневроза Ω в форме пластины размерами 30×300×1 мм, взаимодействующий с шовным материалом диаметрами d  = 0,1 мм, d=0,3 мм, d=0,5 мм.

 

                                         а                                                                                                  б

 

                                         в                                                                                                  г

Рис. 6. Взаимодействие нити с апоневрозом: а - расчётная схема узлового шва, б - расчётная схема непрерывного шва, в - конечно-элементная модель узлового шва, г - конечно-элементная модель непрерывного шва

Таблица 1 Параметры и физические свойства материалов

Материалы	Е, ГПа	n	Размеры, мм
Нить Safil	0,8	0,3	d=0,1 d=0,3 d=0,5
Нить Vicryl	1,4	0,3
Нить PDS 2	2,2	0,3
Нить Monocryl	3,3	0,3
Апоневроз	0,7	0,4	a=30 b=300 c=1

Напряженно-деформированное состояние ткани в рамках линейной теории упругости описывается системой уравнений:

• уравнения равновесия

   (1)

• геометрические соотношения

  ,    (2)

• закон Гука для изотропного тела

 . (3)

Граничные условия имеют вид:

• боковая грань (граница ) апоневроза считаются полностью закрепленными

 ,        

• на части границы задан вектор напряжений t

 ,     

где .

Величина суммарной силы F, действующей на нить равна:

, где d_s - диаметр нити.

На границе  происходит взаимодействие, для описания которого используется теория трения Кулона, где максимальное напряжение сдвига τ_max пропорционально давлению p.

  τ_max = fp; τ ≤fp,     (6)

где f - коэффициент трения. В работе коэффициент трения принимался, равным 0,3 [15].

Решение задачи осуществлялось методом конечных элементов в пакете ANSYS 12. Для разбиения использовались плоские элементы Shell и Plane, а также контактные элементы Conta и Target из библиотеки конечных элементов.

3. Результаты и обсуждение

Результаты решения задачи для узлового шва показаны на рис. 7-9. Следует отметить, что максимальные напряжения возникают в области контакта нити с тканью апоневроза.

На рис. 7 показана зависимость напряжений в апоневрозе от шага ушивки (n = 3, 6, 9 (где n - число стежков)). Из рисунка видно, что при наложении узлового шва уровень напряжений меняется незначительно, т.е. число стежков не оказывает влияние на уровень напряжений в ткани для узлового шва. При узловом шве число стежков является независимым параметром.

На рис. 8 изображена зависимость напряжений в ткани апоневроза от диаметра нити при фиксированном числе стежков (n=6) и постоянной силе, которую прикладывает врач при ушивании (F=50 Н). Из рис. 8 можно заметить, что с увеличением диаметра нити уровень напряжений уменьшается. Данный эффект, по-видимому, связан с увеличением площади контакта между нитью и апоневрозом и перераспределением напряжений в данной области. В медицинской практике известны случаи, когда нить маленького диаметра прорезает ткань и тем самым травмирует её [2].

На рис. 9 (а-в) показаны зависимости σ-F в зависимости от различных диаметров нитей. Из диаграмм можно найти предельные значения силы, которую необходимо приложить к нити при затягивании, чтобы не нарушить микроциркуляторное кровообращение в ткани, соответствующие значению напряжений (σ = 1 кПа), которые представлены в табл. 2.

Результаты по решению задачи для непрерывного шва показаны на рис. 10-12.

На рис. 10 изображена зависимость напряжений в апоневрозе от шага ушивки (n=3, 6, 9 (где n - число стежков)) при наложении непрерывного шва. В данном случае число стежков для непрерывного шва имеет сильное влияние, поскольку при увеличении шага ушивки напряжения перераспределяются по длине ушиваемой раны.

Рис. 7. Зависимость напряжений в ткани апоневроза (σ) от шага ушивки (n) при наложении узлового шва

 

Рис. 8. Зависимость напряжений от диаметра нити при наложении узлового шва (n=6, F=50 Н):
1 - Safil, 2 - Vicryl, 3 - PDS 2, 4 - Monocryl

 

  

 а                                                                                  б

в

Рис. 9. Зависимости напряжений (σ) от силы затяжки (F): 1 - Safil, 2 - Vicryl, 3 - PDS 2, 4 - Monocryl

 

Таблица 2 Предельные силы затяжки в апоневрозе для узлового шва

Нити	Предельная сила затяжки F (H) при dнити=0,1 мм	Предельная сила затяжки F (H) при dнити=0,3 мм	Предельная сила затяжки F (H) при dнити=0,5 мм
Monocryl	4,8	5,7	7,3
PDS 2	5,5	6,5	8,6
Vicryl	6,7	8,2	10,4
Safil	8	9,6	11,8

Рис. 10. Зависимость напряжений в ткани апоневроза (σ) от шага ушивки (n) при наложении непрерывного шва

Рис. 11. Зависимость напряжений от диаметра нити при наложении непрерывного шва (n=6, F=50 Н):
1 - Safil, 2 - Vicryl, 3 - PDS 2, 4 - Monocryl

а                                                                               б

в

Рис. 12. Зависимости напряжений (σ) от силы затяжки (F): 1 - Safil, 2 - Vicryl, 3 - PDS 2, 4 - Monocryl

Таблица 3 Предельные силы затяжки в апоневрозе для непрерывного шва

Нити	Предельная сила затяжки F (H) при dнити=0,1 мм	Предельная сила затяжки F (H) при dнити=0,3 мм	Предельная сила затяжки F (H) при dнити=0,5 мм
Monocryl	18,5	23	28
PDS 2	31	40	53
Vicryl	50	63	81
Safil	75	92	112

 

 а б 

Рис. 13. Сравнение результатов для нити PDS 2: а - непрерывного шва, б - узлового шва

На рис. 11 показана зависимость напряжений в ткани апоневроза от диаметра нити при фиксированном числе стежков (n=6) и постоянной силе, которую прикладывает врач при ушивании (F=50 Н). Также можно заметить, что величина напряжений для непрерывного шва значительно меньше. На рис. 9 (а-в) показаны зависимости σ-F в зависимости от различных диаметров нитей. Из диаграмм можно найти предельные значения силы, которую необходимо приложить к нити при затягивании, чтобы не нарушить микроциркуляторное кровообращение в ткани, соответствующие значению напряжений (σ = 1 кПа), которые представлены в табл. 3.

Из рис. 13 при сравнении результатов для узлового и непрерывного швов видно, что величина напряжений в апоневрозе значительно ниже для непрерывного шва, что позволяет его считать менее травматичным для ткани по сравнению с узловым швом. В результате расчётов показано, что наиболее травматичной является нить Monocryl, а менее травматичной - нить Safil.

Заключение

В работе исследовалось напряженно-деформированное состояние ткани апоневроза при взаимодействии с синтетическим рассасывающимся шовным материалом, активно применяющимся в современной медицине. В ходе исследования были получены зависимости σ-F (напряжения в апоневрозе - сила, прикладываемая к нити), σ-d (напряжения в апоневрозе - диаметр нити) и σ-n (напряжения в апоневрозе - количество стежков).

В результате биомеханического анализа при сравнении двух методов ушивания апоневроза показано преимущество непрерывного шва по сравнению с узловым.

В результате расчётов показано, что наиболее травматичной является нить Monocryl, а менее травматичной - нить Safil.

Полученные результаты можно использовать для разработки практических рекомендаций врачам.

Благодарности

Авторы благодарят сотрудников Центра экспериментальной механики Пермского национального исследовательского политехнического университета
проф. В. Э. Вильдемана и С. В. Словикова за помощь в проведении экспериментов на одноосное растяжение нитей.

Рецензенты:

• Аптуков В. Н., д.т.н., заведующий кафедрой математического анализа ГОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь.
• Попов А. В., д.м.н., профессор кафедры госпитальной хирургии ГОУ ВПО «Пермская государственная медицинская академия им. акад. Е. А. Вагнера», г. Пермь.

---

Библиографическая ссылка

Кучумов А.Г., Самарцев В.А., Чайкина Е.С., Гаврилов В.А. БИОМЕХАНИКА ШОВНЫХ МАТЕРИАЛОВ В АБДОМИНАЛЬНОЙ ХИРУРГИИ // Современные проблемы науки и образования. 2012. № 2. ;
URL: https://science-education.ru/en/article/view?id=5955 (дата обращения: 03.05.2026).