Целью данной работы является исследование антигололёдных свойств асфальторезины, а именно возможности разрушения корки льда, образующейся при гололеде, под воздействием колес проезжающего автотранспорта.
1. Рассмотрим зону пятна контакта колеса с дорожным асфальторезиновым покрытием, на поверхности которого имеется слой льда. Размеры пятна значительно превосходят размеры частиц резины, прослоек асфальта между ними и толщину ледяного слоя. В силу этого при оценке напряженно-деформированного состояния в зоне пятна давления для системы «асфальторезина - лед» будем считать справедливыми следующие предположения:
- частицы резины не имеют преимущественных размеров, а их размещение в асфальторезине является в среднем однородным;
- толщина льда не превосходит средний линейный размер характерного объема асфальторезины;
- материалы структурных элементов (резины, асфальта, льда) являются изотропными и упругими;
- давление колеса p на пятне контакта постоянно;
- поля напряжений и деформаций во всех структурных элементах однородны;
- до разрушения структурные элементы деформируются совместно без отрывов.
В соответствии со сделанными предположениями можно считать, что в зоне пятна контакта с колесом система «асфальторезина - лед» ведет себя как представительный объем, расчетная схема которого показана на рис. 1.
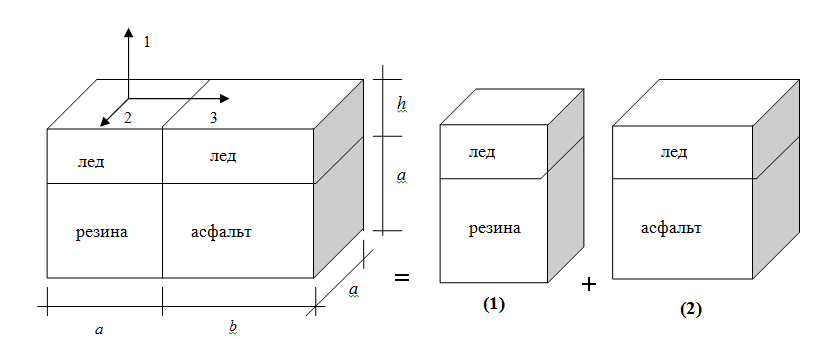
Рис. 1. Расчетная схема представительного объема системы «асфальторезина - слой льда»:
(1) - фрагмент «резина - лед»; (2) - фрагмент «асфальт - лед».
Согласно предположению об однородности физических полей далее под напряжениями и деформациями понимаем их средние значения. Выделим в представительном объеме два фрагмента: «резина - лед» (1) и «асфальт - лед» (2).
Обозначим:
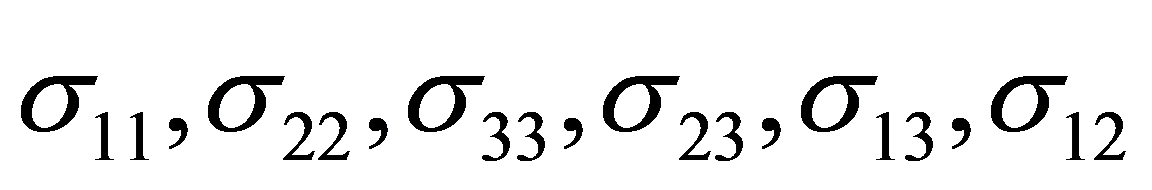 - средние напряжения в представительном объеме;
- средние напряжения в представительном объеме;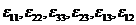 - средние деформации в представительном объеме;
- средние деформации в представительном объеме;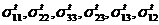 - средние напряжения в объеме t;
- средние напряжения в объеме t; 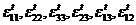 - средние деформации в том же объеме.
- средние деформации в том же объеме.
Здесь верхний индекс следующим образом указывает на объем, по которому произведено осреднение:
t=р - частица резины;
t=а - элемент асфальта;
t=л1 - элемента льда, контактирующего с частицей резины;
t=л2 - элемента льда, контактирующего с элементом асфальта;
t=(1) - фрагмент (1) «резина - лед»;
t=(2) - фрагмент (2) «асфальт - лед».
Введем также матрицы напряжений и деформаций:
![]() ,
, ![]()
![]() ,
, ![]() ,
,
где индекс "T" обозначает операцию транспонирования.
Поставим задачу: найти зависимости напряжений в структурных элементах (микронапряжения) ![]() ,
, ![]() ,
, ![]() ,
, 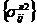 от давления колеса р.
от давления колеса р.
Выделим в представительном объеме два уровня осреднения: на первом осреднение проводим по каждому из фрагментов (1) и (2), рассматривая их как двухкомпонентные среды «резина - лед» и «асфальт - лед»; на втором осреднение проводим по всему представительному элементу, рассматривая его как двухкомпонентную среду, состоящую из фрагментов (1) и (2). При поведении осреднения на каждом уровне используем идею метода осреднения, предложенную в [1] для двухкомпонентной среды.
2. Рассмотрим процедуру осреднения для фрагментов (1) и (2). Условия равновесия и совместности деформаций льда и резины во фрагменте (1) запишем в виде:
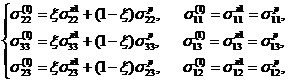 (1)
(1)
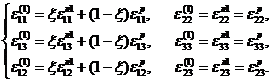 (2)
(2)
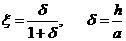 .
.
Здесь параметр ![]() - относительное объемное содержание льда в каждом из структурных элементов (1) и (2).
- относительное объемное содержание льда в каждом из структурных элементов (1) и (2).
Приведенные уравнения отражают правило смеси: вклад компонента пропорционален его объемной доле; при этом уравнения, стоящие в первых столбцах систем (1) и (2), соответствуют осреднению по Рейсу, а во вторых - по Фойхту [2; 7].
В соответствии с принятыми предположениями уравнения состояния материалов льда и резины имеют вид:
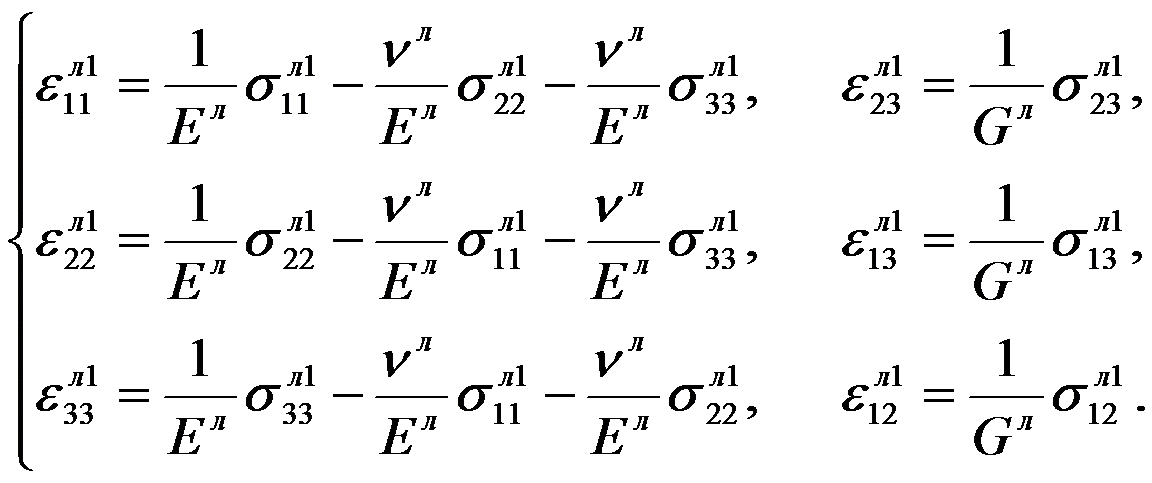 (3)
(3)
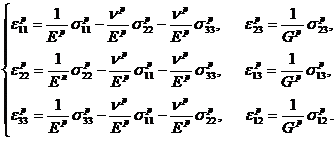 (4)
(4)
где E - модуль Юнга, G - модуль сдвига, v - коэффициент Пуассона льда (л) и резины (р).
Используя уравнения (1) - (4), выразим напряжения в элементах льда { ![]() } и резины {
} и резины {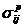 } через напряжения {
} через напряжения { ![]() }, действующие на фрагмент (1) в целом, в виде
}, действующие на фрагмент (1) в целом, в виде
![]() ,
, ![]() , (5)
, (5)
где матрицы 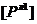 и
и ![]() имеют вид:
имеют вид:
 ,
,  . (6)
. (6)
Здесь
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
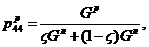
![]()
Далее, исключив из уравнений (1) - (4) компоненты напряжений и деформаций в элементах льда и резины, получим эффективное уравнение состояния двухкомпонентного фрагмента (1):
![]() . (7)
. (7)
Здесь матрица податливостей имеет вид:
 , (8)
, (8)
где
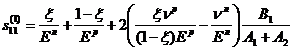 ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, 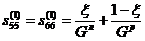 .
.
Для напряжений и деформаций в элементах асфальта и льда во фрагменте (2) справедливы такие же уравнения, как и (1) - (4) для резины и льда во фрагменте (1). Поэтому их можно получить, если в (1) - (4) заменить индексы величин по схеме:
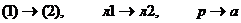 .
.
Как следствие, из (5) получаем зависимости напряжений в элементах асфальта { 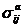 } и льда {
} и льда {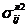 } через напряжения {
} через напряжения {![]() }, действующие на фрагмент (2) в целом, в виде
}, действующие на фрагмент (2) в целом, в виде
![]() , (9)
, (9)
![]() ,
,
а из (4.7) - эффективное уравнение состояния двухкомпонентного фрагмента (2):
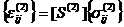 . (10)
. (10)
3. Для представительного объема как двухкомпонентной среды, состоящей из фрагментов (1) и (2), справедливы уравнения равновесия и совместности деформаций:
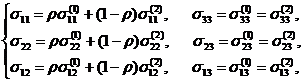 (11)
(11)
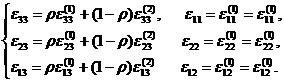 (12)
(12)
где ρ - относительное объемное содержание резины в асфальторезине, определяемое как
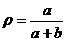 .
.
Из уравнений (7), (10) - (12) выразим напряжения { ![]() }, {
}, {![]() } во фрагментах (1) и (2) через напряжения {
} во фрагментах (1) и (2) через напряжения {![]() }, действующие на представительный объем в целом, в виде
}, действующие на представительный объем в целом, в виде
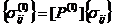 , (13)
, (13)
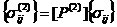 ,
,
где
 ,
,  . (14)
. (14)
![]() ,
, ![]() ,
, ![]() ,
, 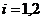 ,
,![]() ,
,
![]() ,
, 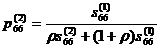 ,
,
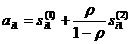 ,
, ![]() ,
, ![]()
![]() - символ Кронекера.
- символ Кронекера.
Далее с помощью (13) исключаем из уравнений (7), (10) - (12) компоненты напряжений и деформаций во фрагментах (1) и (2), получим эффективное уравнение состояния материала представительного объема:
![]() . (15)
. (15)
Здесь матрица податливостей имеет вид:
 , (16)
, (16)
где
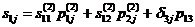 ,
, 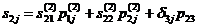 , j=1, 2, 3,
, j=1, 2, 3,
![]() ,
,
![]() ,
, ![]()
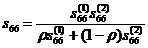 .
.
4. Будем считать, что в зоне пятна контакта в представительном объеме выполняются условия:
1) ![]() ,
, 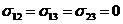 ,
,
где р - давление колеса автомобиля;
2) деформации в направлении осей координат 2 и 3 полностью стеснены:
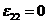 ,
, ![]() .
.
При этих условиях из уравнения (15) находим:
![]() ,
, 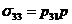 ,
,
где
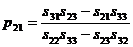 ,
, ![]() .
.
Следовательно, матрица средних напряжений в представительном объеме имеет вид:
![]() . (17)
. (17)
где ![]() .
.
В итоге согласно соотношениям (5), (9), (13) (17) напряжения в элементах льда, резины и асфальта связаны с давлением колеса в зоне пятна контакта соотношениями
![]() ,
, 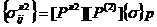 , (18)
, (18)
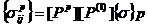 ,
, 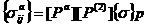 .
.
Таким образом, поставленная задача решена.
5. Для оценки прочности материалов асфальта, резины и льда введем показатель напряжений:
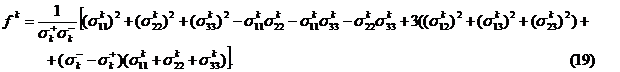
где 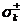 - предел прочности материала в структурном элементе k на растяжение (+) и сжатие (-); индекс k принимает значения: л1, л2, р, а.
- предел прочности материала в структурном элементе k на растяжение (+) и сжатие (-); индекс k принимает значения: л1, л2, р, а.
Согласно критерию прочности Баландина [3] разрушение в материале происходит, если
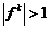 .
.
Результаты расчетов величин 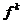 по формулам (18), (19) в зависимости от интенсивности наполнения асфальторезины ρ представлены на рис. 2. Для расчета приняты значения:
по формулам (18), (19) в зависимости от интенсивности наполнения асфальторезины ρ представлены на рис. 2. Для расчета приняты значения: ![]() 500 МПа,
500 МПа, ![]() 5 МПа,
5 МПа, ![]() 5500 МПа,
5500 МПа, ![]() 0,3,
0,3, 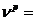 0,5,
0,5, 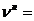 0,35,
0,35, ![]() =1,4 МПа,
=1,4 МПа,![]() =13 МПа,
=13 МПа, ![]() =14 МПа,
=14 МПа, ![]() =2,5 МПа
=2,5 МПа ![]() =0,3 МПа,
=0,3 МПа,![]() =2,5 МПа; толщина ледяного слоя h=3 мм, линейный размер резиновой крошки a=8 мм.
=2,5 МПа; толщина ледяного слоя h=3 мм, линейный размер резиновой крошки a=8 мм.
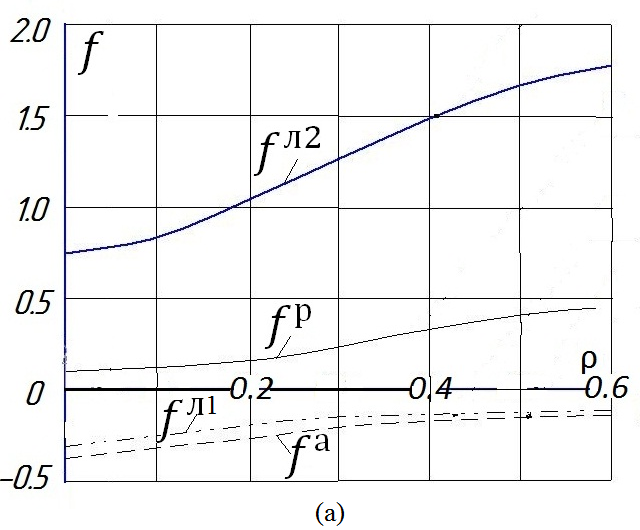
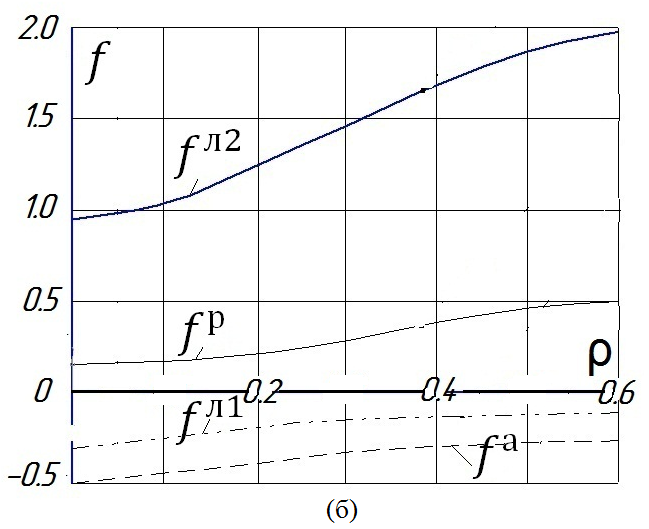
Рис. 2. Зависимость уровня напряжений ![]() в элементах представительного объема системы «асфальторезина - лед» от объемного содержания резины ρ при действии давления колеса автомобиля р:
в элементах представительного объема системы «асфальторезина - лед» от объемного содержания резины ρ при действии давления колеса автомобиля р:
(а) - легковой автомобиль (р=0,25 МПа); (б) - грузовой автомобиль (р=0,35 МПа).
Из приведенных графиков видно, что при внешнем равномерном давлении уровни напряжений во фрагменте льда, контактирующем с частицей резины, и фрагменте льда, контактирующем с элементом асфальта, различаются, причем во втором он значительно выше. Если объёмное содержание резины ![]() , то при значении давления, соответствующего весу легкового автомобиля, уровень напряжений в этом фрагменте превышает критическое значение, что означает его разрушение; давление колеса грузового автомобиля вызовет аналогичное разрушение льда, если
, то при значении давления, соответствующего весу легкового автомобиля, уровень напряжений в этом фрагменте превышает критическое значение, что означает его разрушение; давление колеса грузового автомобиля вызовет аналогичное разрушение льда, если ![]() .
.
Таким образом, введение резиновой крошки в асфальт вызывает значительное перераспределение напряжений в гололедном слое на поверхности дорожного полотна, что приводит к разрушению льда под воздействием колес проходящего транспорта.
Рецензенты
- Кошур Владимир Дмитриевич, доктор физико-математических наук, профессор, зав. лабораторией вычислительного эксперимента, профессор кафедры вычислительной техники, Институт космических и информационных технологий, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
- Лозовой Владимир Андреевич, доктор технических наук, профессор, заведующий кафедрой технологии и оборудования лесозаготовок Сибирского государственного технологического университета, г. Красноярск.



