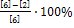Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Целью настоящего исследования является разработка инженерно-ориентированного метода оценки эксплуатационного состояния, несущей способности, а также проектного или остаточного ресурса коррозионно-поврежденных изгибаемых железобетонных элементов.

Диахронная модель рассматривает напряженно-деформированное состояние изгибаемого железобетонного элемента с симметричным в плоскости изгиба поперечным сечением площадью S и двойным армированием. В случае поперечного изгиба предполагается превалирующей роль изгибающего момента M и продольного усилия N при пренебрежимом влиянии перерезывающих сил. Образование и развитие системы нормальных трещин в растянутой зоне бетона происходит при достижении момента трещинообразования M_crc. Преимущественно трещины располагаются на примерно одинаковом расстоянии - L_crc = 2L одна от другой, имеют почти одинаковую глубину h_crc и ширину раскрытия a_crc (рис. 1).

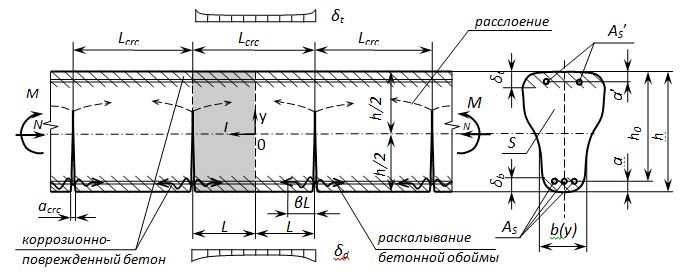
Рис. 1. Схема элемента при силовых и коррозионных воздействиях

Далее изгибаемый элемент рассматривается как детерминировано-регулярная контактная система деформируемых блоков, разделенных равноотстоящими трещинами. Блоки взаимодействуют в области сохраняющего сплошность бетона, а также посредством сжатой A'_s и растянутой A_s стержневой арматуры. При этом напряженно-деформированное состояние нетрещиностойкого элемента является циклически симметричным относительно характерных сечений двух типов: с трещинами (l=±L) и равноудаленных от смежных трещин-близнецов (l=0). При таком подходе проблема определения напряженно-деформированного состояния элемента сводится к решению задачи для симметричной половины S x L характерного блока [2, 3].

Основными факторами негативного влияния агрессивных воздействий на железобетонный элемент являются:

• деградация прочностных и деформационных свойств сжатого и растянутого бетона;
• коррозия арматурных стержней;
• повреждения сцепления растянутой арматуры с бетоном;

Изменение геометрических и механических параметров бетона зависит от направленности агрессивного воздействия - с боковых граней сечения δ_s, со стороны сжатой δ_t и / или растянутой зоны δ_b, а также вида и интенсивности агрессии. Изменчивость свойств бетона по глубине схематизируется трехзонной моделью:

• полностью разрушенный бетон (уменьшение начальных габаритов сечения);
• слой частично-поврежденного бетона, в пределах которого деформационные (E_b, e_bu, e_btR) и прочностные (R_b, R_bt) характеристики линейно изменяются - от нулевого (минимального) до номинального значения;
• неповрежденный бетон, сохранивший номинальные характеристики.

При отсутствии полностью разрушенного бетона пониженные характеристики краевых волокон бетона эксплуатируемых сооружений устанавливаются по результатам технического обследования. Для проектируемых сооружений аналогичные параметры определяются в соответствии с принятыми моделями деградации (например, диссипативная модель В. М. Бондаренко, степенные функции А. И. Попеско [4]).

Одновременно, за счет снижения начального модуля деформации E_b, сопротивлений R_b, R_bt и базовых деформаций ε_R и ε_b ul в пределах коррозионно-поврежденного слоя трансформируются исходные диаграммы деформирования сжатого и растянутого бетона (рис. 2).

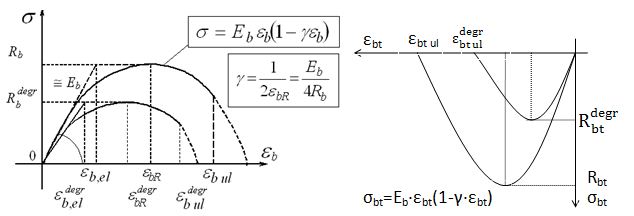
Рис. 2. Трансформация диаграмм деформирования бетона при сжатии и растяжении

Изменение модуля деформации бетона E_b,ar,c описывается степенной функцией с коэффициентами аппроксимации, полученной методами регрессионного анализа:  (t - время воздействия, a_E, b_E - эмпирические коэффициенты).

Равномерная и питтинговая коррозия металла отражается независимым либо согласованным (в зависимости от направленности и характера агрессивного воздействия) уменьшением исходных поперечных сечений растянутой A_s и сжатой A'_s арматуры, с учетом неравномерности коррозии арматуры по длине блока.

Учитывается влияние уровня напряжений и вида напряженного состояния на скорость проникновения агрессивных веществ в тело бетона. Так, усиленная деструкция бетона имеет место в сечении с трещиной. За счет прямого доступа агрессивных сред через раскрытую трещину здесь формируется и локальный максимум потери площади растянутой арматуры (рис. 1).

Коррозионные повреждения контактной системы «арматура-бетон» обусловлены суперпозицией избыточного давления продуктов коррозии арматуры, превышающих первоначальный объем металла в 2-4 раза, и расклинивающего эффекта при выходе профилированного арматурного стержня из бетона. Сложный физический процесс моделируются путем трансформации закона сцепления «τ_сц - g» и снижения длины активного сцепления.

Локальный закон сцепления трансформируется в соответствии с [6] за счет введения дополнительных смещений арматуры относительно бетона , где Δr_s - глубина коррозии арматуры, m - эмпирический коэффициент. При этом исходный график функции «τ_сц - g» как жесткое целое смещается в отрицательную область оси абсцисс -  на .

При проведении практических расчетов критические распорные и касательные напряжения определялись по упрощенным зависимостям [5].

Критерием образования вторичных продольных трещин, исходящих из вершин поперечных и обусловливающих прогрессирующее расслоение элемента, принимается . Откалывающие напряжения σ_spl (рис. 3) определяются как:

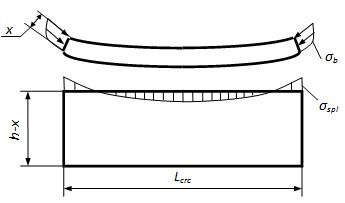
Рис. 3. Расчетная схема расслоения элемента

Ширину раскрытия пионерной трещины a_crc и шаг трещин L_crc определяются в соответствии с мультиплексной моделью сцепления Gambarova P. G.:

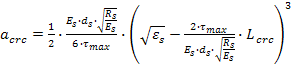  (1)

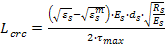 (2)

Выполнена верификация предлагаемой диахронной модели с лабораторными испытаниями разных авторов: Maaddawy T. E., Mangat P. S. и Попеско А.И [4] (таблица 1).

Таблица 1. Схемы экспериментов

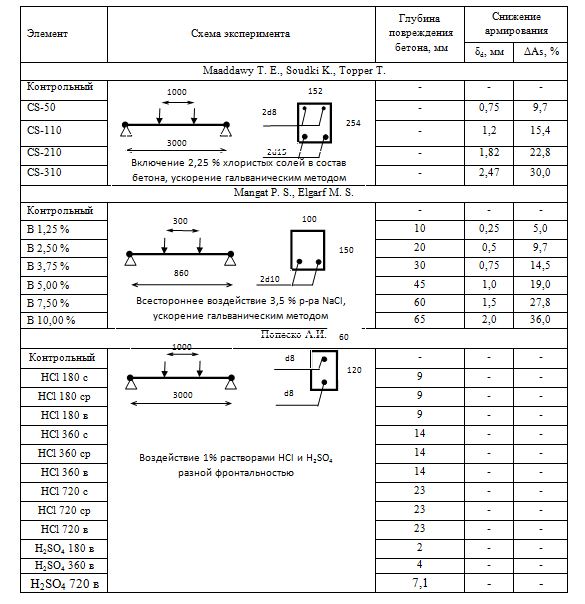
Результаты лабораторных экспериментов и расчетов по диахронной модели сведены в таблицу 2. Отклонение результатов расчетов разрушающего изгибающего момента M_ult не превышают 12 %, среднеквадратическое отклонение составило 8,9 %. Отклонение результатов расчетов прогиба f находится в пределах 30 %, среднеквадратическое отклонение составило 22,4 %. Важно отметить, что фактический и прогнозируемый по диахронной модели вид разрушения совпадают. Ввиду хорошего соответствия теоретических и фактических результатов можно рекомендовать диахронную модель для применения в инженерной практике.

Таблица 2. Сравнение экспериментальных и теоретических результатов

Предлагаемая диахронная модель позволяет определить ресурс железобетонных элементов работающих при совместном силовом и коррозионном воздействиях. Решение задачи ведется графо-аналитически в следующей последовательности:

1. В разрешающие уравнения вводятся принятые характеристики бетона и арматуры, габариты сечения.
2. На основании данных об агрессивной среде эксплуатации по реономным моделям деградации бетона и арматуры определяется физико-механические свойства материалов в моменты времени t₁, t₂, t₃ и т. д. При ожидаемом сроке службы, например, 50 лет, принимаются t₁=0, t₂=25, t₃=50 годам.
3. Определение напряженно-деформированного состояния элемента и предельного момента M_ult1, M_ult2, M_ult3 и т.д. и всех других параметров оценки наступления предельных состояний во время соответственно - t₁, t₂, t₃ и т.д.

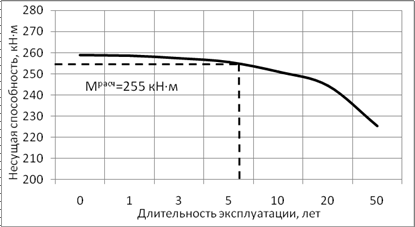
Рис. 4. Прогнозируемая несущая способность ригеля РДП 4.56-70 AIIIв

По предложенной методике определен срок службы ригеля серии 1.020-1/87, работающего в агрессивной промышленной среде. Выявлено, что даже при нормативных показателях рабочей среды (паров H₂SO₄ до 0,145 мг/л, H₂S до 0,01 мг/л и CS₂ до 0,03 мг/л при относительной влажности 80-85 %) происходит существенное снижение несущей способности рассматриваемого ригеля - до 12,4 % за 50 лет (рис. 4). Срок службы рассматриваемого ригеля составляет 6,5 лет. Для обеспечения нормативного срока эксплуатации 50 лет рекомендовано применение вторичной защиты.

Предполагая неизменным характер и интенсивность деградационного воздействия окружающей среды, с помощью диахронной модели деформирования, задаваясь реономными моделями деградации бетона и арматуры, возможно прямое определение проектного ресурса вновь возводимых и остаточный ресурс эксплуатируемых изгибаемых железобетонных конструкций по наступлению следующих предельных состояний:

• достижение растянутой арматурой в трещине предела текучести по условию s_s=R_s;
• исчерпание несущей способности сжатого бетона в сечении с трещиной по условиям e_b=e_bul либо s_b=R_b;
• разрушение системы сцепления из условия β=1;
• расслоение элементов с образованием и развитием вторичных трещин, исходящих из вершин пионерных трещин, по условию s_z=R_bt;
• чрезмерность раскрытия трещин а_crc=a_crc,ult.

Важно отметить, что применение такой методики впервые открывает возможность актуального повышения экономической эффективности проектных решений путем обеспечения однородной долговечности железобетонных конструкций с синхронизацией проектного ресурса отдельных зон, элементов и частей зданий и сооружений.

Рецензенты:

• Белов В. В., д.т.н., главный специалист по железобетонным конструкциям ОАО «Санкт-Петербургский НИПКИ "Атомэнергопроект"», г. Санкт-Петербург.
• Лалин В. В., д.т.н., профессор, зав. каф. СМиТУ ФГБОУ ВПО «СПбГПУ», г. Санкт-Петербург.