Установившееся потенциальное движение воды, обтекающей корпус судна, может быть представлено следующим уравнением [5]:
|
|
(1) |
Здесь ![]() - ускорение свободного падения;
- ускорение свободного падения;
z - аппликата рассматриваемой точки потока;
p - давление жидкости в данной точке;
ρ - плотность жидкости;
![]() - скорость жидкости в данной точке.
- скорость жидкости в данной точке.
Следовательно, уравнение (1) может рассматриваться как интеграл Громеки [4] (или как уравнение Бернулли) применительно к случаю обтекания корпуса судна реальной жидкостью.
Перепишем выражение (1) следующим образом:
|
|
(2) |
где z1, z2 - аппликаты рассматриваемых точек потока, обтекающего корпус судна;
p1 , p2 - давления жидкости в рассматриваемых точках потока;
![]() - скорости частиц жидкости в рассматриваемых точках потока.
- скорости частиц жидкости в рассматриваемых точках потока.
Если рассматриваемые точки потока, обтекающего корпус судна, лежат в одной и той же плоскости ватерлинии (то есть ![]() ), то выражение (2) примет следующий вид:
), то выражение (2) примет следующий вид:
|
|
(3) |
Уравнение (3) позволяет определять разность давлений реальной жидкости на поверхности обшивки корпуса судна, возникающую как вследствие разности скоростей их обтекания, так и вследствие разности гидродинамических напоров на эти поверхности.
Элементарное гидродинамическое усилие ![]() , действующее на поверхность обшивки погруженной части судового корпуса в какой-либо точке
, действующее на поверхность обшивки погруженной части судового корпуса в какой-либо точке ![]() , может быть представлено в виде
, может быть представлено в виде
|
|
(4) |
Здесь dS - элементарная площадь смоченной поверхности корпуса.
Проецируя силу dQ на продольную x и поперечную y оси связанной с судном системы координат, получаем:
|
|
(5) |
|
|
(6) |
где q - двугранный угол между диаметральной плоскостью (ДП) судна и вертикальной плоскостью, проходящей через нормаль к ватерлинии в рассматриваемой точке ![]() . Поскольку в данной работе угол q отличается от принятого в навигации [3] курсового угла лишь тем, что всегда положителен, то в дальнейшем будем называть угол q курсовым углом нормали, подразумевая, что он измеряется в четвертной системе счёта;
. Поскольку в данной работе угол q отличается от принятого в навигации [3] курсового угла лишь тем, что всегда положителен, то в дальнейшем будем называть угол q курсовым углом нормали, подразумевая, что он измеряется в четвертной системе счёта;
![]() - снижение нормали к поверхности корпуса в этой точке относительно нормали к ватерлинии.
- снижение нормали к поверхности корпуса в этой точке относительно нормали к ватерлинии.
Произведения ![]() ,
, ![]() представляют собой проекции элементарной площади dS соответственно на плоскость мидельшпангоута и ДП судна, то есть:
представляют собой проекции элементарной площади dS соответственно на плоскость мидельшпангоута и ДП судна, то есть:
|
|
(7) |
|
|
(8) |
Подставив равенства (7) и (8) в уравнения (5) и (6), получим:
|
|
(9) |
|
|
(10) |
Следовательно, в случае плоскопараллельного движения судна проекции действующих на его корпус элементарных гидродинамических усилий будут определяться выражениями:
|
|
(11) |
|
|
(12) |
В уравнениях (11) и (12) обозначено:
![]() - проекции элементарной гидродинамической силы, приложенной к корпусу судна, на оси подвижной системы координат;
- проекции элементарной гидродинамической силы, приложенной к корпусу судна, на оси подвижной системы координат;
![]() - разность динамических давлений жидкости в равноотстоящих от ДП и лежащих в плоскости одной и той же ватерлинии точках обшивки носовой и кормовой оконечностей судового корпуса;
- разность динамических давлений жидкости в равноотстоящих от ДП и лежащих в плоскости одной и той же ватерлинии точках обшивки носовой и кормовой оконечностей судового корпуса;
![]() - разность динамических давлений жидкости в симметричных относительно ДП точках обшивки внешнего и внутреннего бортов корпуса судна.
- разность динамических давлений жидкости в симметричных относительно ДП точках обшивки внешнего и внутреннего бортов корпуса судна.
Выражения (11) и (12) позволяют сделать предположение о том, что для определения действующих на судно гидродинамических усилий существует объективная возможность замены реального судового корпуса его эквивалентным аналогом.
Действительно, разделим погруженный объем корпуса судна на три составные части:
1) цилиндрическая вставка - средняя часть корпуса, характеризующаяся постоянством значения коэффициента полноты;
2) носовая оконечность - часть корпуса, расположенная в нос от цилиндрической вставки;
3) кормовая оконечность - часть корпуса, расположенная в корму от цилиндрической вставки.
Кроме того, представим реальный корпус судна в виде некоего условного корпуса с вертикальными штевнями. Тогда при сохранении объёмов его составных частей значения длины и коэффициента полноты водоизмещения носовой оконечности будут:
|
|
(13) |
а кормовой:
|
|
(14) |
где ![]() - средняя длина носовой оконечности корпуса судна;
- средняя длина носовой оконечности корпуса судна;
![]() - коэффициент полноты носовой половины диаметрального батокса;
- коэффициент полноты носовой половины диаметрального батокса;
L - длина судна;
![]() - средняя длина цилиндрической вставки в носовой половине корпуса;
- средняя длина цилиндрической вставки в носовой половине корпуса;
![]() - коэффициент полноты водоизмещения носовой оконечности корпуса;
- коэффициент полноты водоизмещения носовой оконечности корпуса;
![]() - коэффициент полноты водоизмещения судна;
- коэффициент полноты водоизмещения судна;
![]() - абсцисса центра масс судового корпуса;
- абсцисса центра масс судового корпуса;
![]() - коэффициент полноты мидельшпангоута;
- коэффициент полноты мидельшпангоута;
![]() - средняя длина кормовой оконечности корпуса судна;
- средняя длина кормовой оконечности корпуса судна;
![]() - коэффициент полноты кормовой половины диаметрального батокса;
- коэффициент полноты кормовой половины диаметрального батокса;
![]() - средняя длина цилиндрической вставки в кормовой половине корпуса;
- средняя длина цилиндрической вставки в кормовой половине корпуса;
![]() - коэффициент полноты водоизмещения кормовой оконечности корпуса.
- коэффициент полноты водоизмещения кормовой оконечности корпуса.
Очевидно, что общий объём погруженной части корпуса судна при этом не меняется, ибо
|
|
(15) |
Здесь B - расчётная ширина судового корпуса;
T - расчётная осадка судна;
![]() - средняя длина цилиндрической вставки корпуса;
- средняя длина цилиндрической вставки корпуса;
|
|
|
Необходимо отметить, что условный корпус, характеризующийся равенством (15), геометрически эквивалентен погруженной части реального судового корпуса.
Для определения зависимости величины ![]() от геометрических характеристик корпуса судна рассмотрим его обращённое движение в продольном направлении с установившейся скоростью
от геометрических характеристик корпуса судна рассмотрим его обращённое движение в продольном направлении с установившейся скоростью ![]() . Спроецировав скорость
. Спроецировав скорость ![]() на внутренние нормали к поверхности в каких-либо равноотстоящих от ДП точках обшивки носовой и кормовой оконечностей корпуса, получим:
на внутренние нормали к поверхности в каких-либо равноотстоящих от ДП точках обшивки носовой и кормовой оконечностей корпуса, получим:
|
|
(16) |
где ![]() - разность давлений, возникающая из-за разности скоростных напоров жидкости на поверхности носовой и кормовой оконечностей корпуса;
- разность давлений, возникающая из-за разности скоростных напоров жидкости на поверхности носовой и кормовой оконечностей корпуса;
![]() - курсовые углы нормалей к ватерлинии в рассматриваемых точках носовой и кормовой оконечностей.
- курсовые углы нормалей к ватерлинии в рассматриваемых точках носовой и кормовой оконечностей.
![]() - снижение нормалей к поверхностям относительно нормалей к ватерлинии в рассматриваемых точках носовой и кормовой оконечностей корпуса.
- снижение нормалей к поверхностям относительно нормалей к ватерлинии в рассматриваемых точках носовой и кормовой оконечностей корпуса.
Найдем приходящееся на единицу площади смоченной поверхности корпуса среднее динамическое давление ![]() в случае установившегося продольного движения судна. Для этого, воспользовавшись теоремой о среднем значении интеграла [1], представим выражение (16) следующим образом:
в случае установившегося продольного движения судна. Для этого, воспользовавшись теоремой о среднем значении интеграла [1], представим выражение (16) следующим образом:
|
|
(17) |
В последнем соотношении обозначено:
![]() - площади смоченных поверхностей носовой и кормовой оконечностей корпуса;
- площади смоченных поверхностей носовой и кормовой оконечностей корпуса;
![]() - коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в носовой оконечности корпуса;
- коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в носовой оконечности корпуса;
![]() - коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в кормовой оконечности судна.
- коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в кормовой оконечности судна.
Следовательно, в случае произвольного установившегося плоскопараллельного движения зависимость ![]() от геометрических характеристик корпуса, согласно формулам Эйлера [2], может быть представлена в виде:
от геометрических характеристик корпуса, согласно формулам Эйлера [2], может быть представлена в виде:
|
|
(18) |
Для оценки зависимости величины ![]() от геометрических характеристик погруженной части корпуса рассмотрим обращённое установившееся поперечное движение судна со скоростью
от геометрических характеристик погруженной части корпуса рассмотрим обращённое установившееся поперечное движение судна со скоростью ![]() . Проецирование скорости
. Проецирование скорости ![]() на внутренние нормали к поверхностям в симметричных относительно ДП точках обшивки бортов даёт следующий результат:
на внутренние нормали к поверхностям в симметричных относительно ДП точках обшивки бортов даёт следующий результат:
в носовой оконечности корпуса
|
|
(19) |
в кормовой оконечности корпуса
|
|
(20) |
в области цилиндрической вставки
|
|
(21) |
Здесь ![]() - коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в области цилиндрической вставки.
- коэффициент, учитывающий среднее снижение нормалей к поверхности обшивки относительно нормалей к ватерлиниям в области цилиндрической вставки.
Таким образом, в случае произвольного установившегося плоскопараллельного движения зависимость ![]() от геометрических характеристик корпуса, согласно формулам Эйлера, может быть представлена в виде:
от геометрических характеристик корпуса, согласно формулам Эйлера, может быть представлена в виде:
|
|
(22) |
|
|
(23) |
|
|
(24) |
Тогда, согласно уравнениям (11) и (12),
|
|
(25) |
|
|
(26) |
где ![]() - разности давлений жидкости на поверхности носовой и кормовой оконечностей соответственно внешнего и внутреннего бортов.
- разности давлений жидкости на поверхности носовой и кормовой оконечностей соответственно внешнего и внутреннего бортов.
Определим моменты этих сил относительно вертикальной оси z. Момент ![]() продольной силы X найдём по выражению:
продольной силы X найдём по выражению:
|
|
(27) |
Аналогично может быть подсчитан и момент ![]() поперечной силы Y -
поперечной силы Y -
|
|
(28) |
Необходимо отметить, что как для реального судового корпуса, так и для его эквивалентного аналога величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() будут иметь одни и те же значения. Поэтому и разности давлений
будут иметь одни и те же значения. Поэтому и разности давлений ![]() ,
, ![]() ,
, ![]() и
и ![]() будут определяться одними и теми же выражениями (18), (22), (23) и (24). Данное обстоятельство позволяет сделать вывод о том, что гидродинамические усилия, действующие как на корпус реального судна, так и на его эквивалентный аналог, тождественны. Следовательно, геометрически эквивалентный аналог одновременно является гидродинамически адекватным аналогом реального судового корпуса.
будут определяться одними и теми же выражениями (18), (22), (23) и (24). Данное обстоятельство позволяет сделать вывод о том, что гидродинамические усилия, действующие как на корпус реального судна, так и на его эквивалентный аналог, тождественны. Следовательно, геометрически эквивалентный аналог одновременно является гидродинамически адекватным аналогом реального судового корпуса.
Таким образом, можно считать доказанным существование объективной возможности для разработки аналитических методов определения действующих на судно гидродинамических усилий. И для того чтобы воспользоваться этой возможностью, необходимо представить погруженную часть судового корпуса в виде её эквивалентного аналога, а значения его геометрических характеристик ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() определить численными методами с помощью теоретического чертежа судна.
определить численными методами с помощью теоретического чертежа судна.
Рецензенты:
Клементьев А.Н., д.т.н. профессор, зав. кафедрой судовождения и безопасности судоходства ФБОУ ВПО «Волжская государственная академия водного транспорта», г. Нижний Новгород.
Тихонов В.И., д.т.н. профессор кафедры судовождения и безопасности судоходства ФБОУ ВПО «Волжская государственная академия водного транспорта», г. Нижний Новгород.




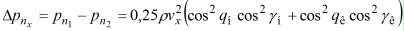 ,
,
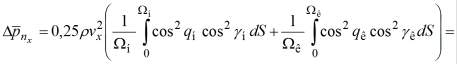
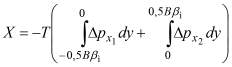 ;
;
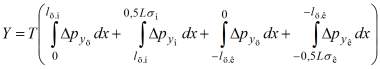 ,
,
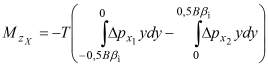 .
.
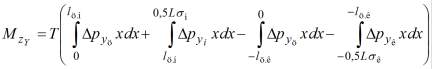 .
.