Установление особенностей течения металла при качении ролика по деформируемой упруго-пластической поверхности может быть основано на понятии о связях, наложенных на материальные точки, которые расположены на заданной поверхности. При условии наложения связей действительное перемещение точек поверхности детали в выбранной системе координат равно геометрической сумме их совместного перемещения с соприкасаемыми точками ролика и дополнительного смещения этих же точек относительно поверхности ролика. Вся проблема заключается в установлении этой второй составляющей.
В процессе качения дуги окружности, образуемой при сечении ролика и детали плоскостью, перпендикулярной оси ролика, при отсутствии проскальзывания, нижняя точка О той же окружности (рис.1) является мгновенным центром вращения, то есть неподвижной относительно деформируемой поверхности.
Скорость любой другой точки М (х,z) дуги окружности ролика, находящейся в контакте с деформируемой поверхностью равна:
VM=ωP×ρм (1)
где: ρм - радиус-вектор, проведенный из точки О в точку М (х,у).
Касательная Vкм и нормальная Vnм - составляющие этого вектора к дуге указанной окружности - определяются из равенств:
Vn =Vм × cos θ; Vk =Vм × sin θ (2)
где: θ - угол между радиусом-вектором×ρм, проведенным из центра окружности Ор в точку М(х,у), и направлением скорости Vм, перпендикулярным радиус-вектору ρм.
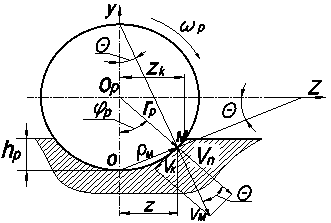
Рис.1. Схема для определения кинематики точек деформируемой поверхности вала без проскальзывания
Для функций sin θ и cos θ имеем следующие соотношения:
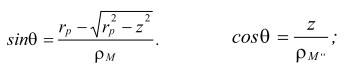 (3)
(3)
С учетом этих соотношений получим:
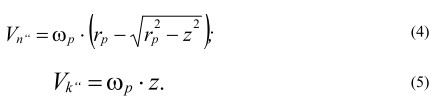
Для вычисления траекторий, по которым движутся точки поверхности ролика, сделаем подстановки:
![]() ,
,
где φр - угол контакта, проведенный из центра ролика в точку М([x,y).
Таким образом:
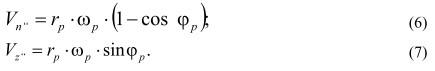
Поскольку:
![]()
где t - время перекатывания ролика по поверхности детали, то, интегрируя (6) и (7) по времени, получим:
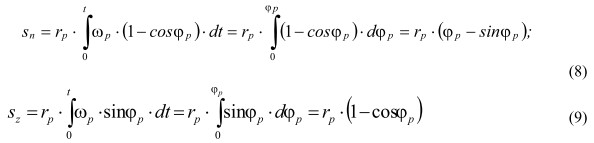
Последние два значения интегралов являются уравнениями циклоид, заданных в параметрической форме.
Поле перемещений точек деформируемой поверхности, описываемое циклоидами (8) и (9), является граничным в том смысле, что действительные траектории не могут быть расположены левее, чем эти траектории. В противном случае, составляющие перемещения будут направлены против сил, выталкивающих металл из зоны обработки, а это невозможно, так как течение металла должно быть направлено в сторону роста напряжений.
Рассмотрим перемещение точек деформируемой поверхности перпендикулярно дугам окружностей, образуемых в сечении ролика при его качении (рис.2, а). В этом случае дуги окружностей представляют семейство, описываемое уравнением:
![]() (10)
(10)
где: s - параметр семейства окружностей.
В предположении, что точки обрабатываемой поверхности перемещаются перпендикулярно поверхности ролика, заключаем, что их траектории движения совпадают с ортогональными линиями семейства (10).
Для определения уравнения семейства ортогональных кривых продифференцируем уравнение (10) по z:
![]() (11)
(11)
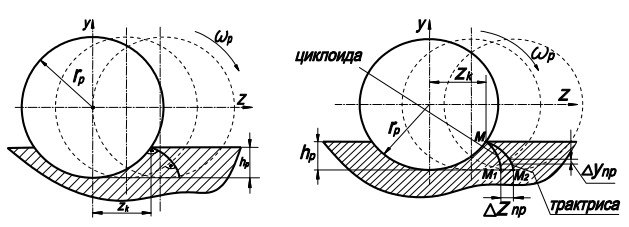
а) б)
Рис.2. Схема для определения траекторий движения точек деформируемой поверхности перпендикулярно поверхности ролика. Сравнение движения точек деформируемой поверхности по циклоидам и трактрисам
Исключив из двух уравнений (10) и (11) параметр s, получим уравнение:
![]() (12)
(12)
которое определяет семейство линий, касательных к семейству (10). Заменив в уравнении (12) y′ на 1/y′, получим:
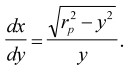
Интеграл этого уравнения определяет семейство траекторий точек деформируемой поверхности в плоскости сечения следующего вида:
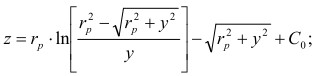 (13)
(13)
где: С0 - постоянная характеризующая конкретную точку поверхности детали. Это уравнение трактрисы. В параметрической форме это же уравнение будет иметь вид:
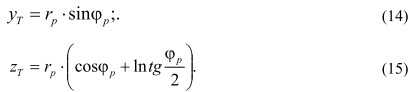
Совместим начала циклоид и трактрис в одной точке М, расположенной на поверхности ролика (рис.2,б).
Из рисунка видно, что движение по трактрисе можно осуществить в виде суммы двух перемещений: перемещение по участку циклоиды от точки М до М2, а затем по дуге окружности - от М1 до М2. В горизонтальном направлении величина сдвига равна:
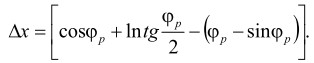 (16)
(16)
Наличием сдвига поверхностного слоя можно объяснить возникновение при ППД преимущественно остаточных напряжений сжатия, т.к. в процессе обработки наружный слой растягивается, причем, чем меньше диаметр ролика при одной и той же глубине внедрения, тем больше растяжение поверхностного слоя.
Аналогичная картина будет наблюдаться для любых других кривых, расположенных правее циклоид.



