Цифровой адаптивный фильтр (ЦАФ) реализован на основе адаптивного устройства подавления помех. На рисунке 1 представлена схема фильтра.
На вход устройства («Входной сигнал») может подаваться сигнал d(t), представляющий собой сумму фильтруемого (полезного) сигнала x(t)=Acos(2πf0t+φ) и комбинации сигналов любого вида - случайных (шум), детерминированных, периодических (активные помехи, работа других передатчиков в полосе частот) и т.п. На эталонном входе («Эталон») действует моногармонический сигнал xэ(t)=Ccos(2πf0t+φ).
Отсчеты входных сигналов берутся с интервалом Tсекунд, после чего переходим к дискретной форме сигналов: dk-входной сигнал, x1k-эталонный сигнал, x2k-эталонный сигнал, сдвинутый на 90º, εk, yk-отсчеты выходного сигнала (k=1,2,3,....).
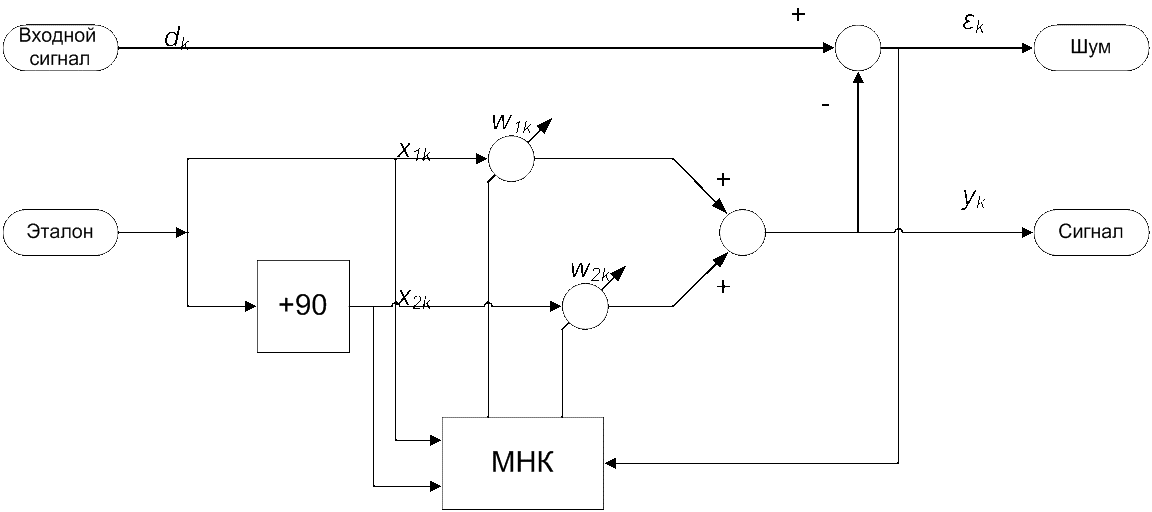
Рисунок1- схема цифрового адаптивного фильтра
Заметим, что названия выходов - «Сигнал» и «Шум» - являются условными. В рассматриваемом случае будем полагать, что эталонный генератор задает полезную составляющую входного сигнала. В противном случае, выходы - «Сигнал» и «Шум» -поменяются местами.
В рассматриваемом фильтре адаптивными (перестраиваемыми) параметрами являются два весовых коэффициента w1 и w2, которые после завершения процесса адаптации принимают значения, приводящие СКО к нулю.
Текущие значения весовых коэффициентов вычисляются методом наименьших квадратов (МНК) по формулам:
,
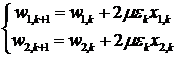где µ - параметр сходимости алгоритма адаптации.
Исходя из выражения , алгоритм настройки коэффициентов может быть реализован с помощью простой схемы, приведенной на рисунке 2. Блоки на рисунке являются стандартными блоками MATLAB/Simulink.
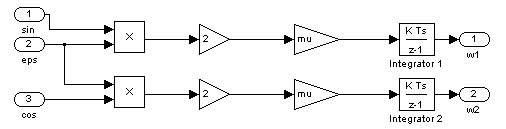
Рисунок 2 - реализация алгоритма настройки коэффициентов в Simulink
В статье [1] также приводятся частотные характеристики данного фильтра (см. рис. 3) для выходов - «Сигнал» и «Шум» - и доказывается устойчивость данной системы.
Пусть теперь полезный сигнал на входе представленного фильтра является сигналом с ФМн-2[2]: последовательность «0» и «1» передается с помощью модуляции фазы несущей частоты, при этом фаза принимает одно из двух значений 
Если сигнал с ФМн-2 используется совместно с расширением спектра методом прямой последовательности, то ширина спектра входного сигнала равна 
, где T - минимальное время, в течение которого фаза остается постоянной или «длительность чипа».
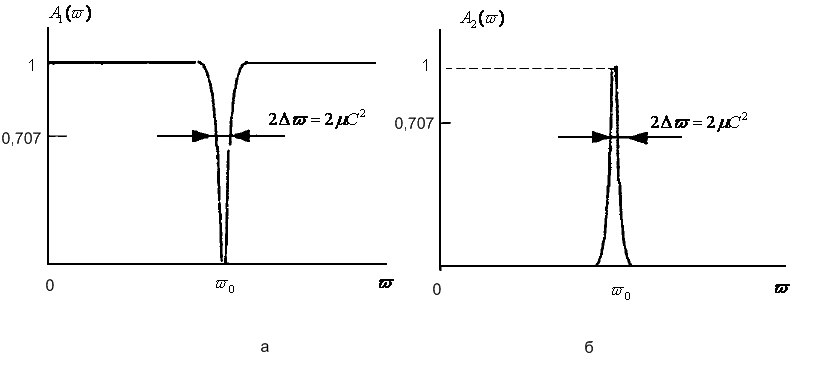
Рисунок 3 - частотные характеристики фильтра: а) - на выходе «Шум», б) - на выходе «Сигнал»
В этом случае из-за постоянных переключений фазы адаптивные коэффициенты 
не будут стремиться к некоторому постоянному значению. Кроме того, т.к. длительность чипа обычно достаточно мала (а значит, велика требуемая полоса пропускания фильтра), придется выбирать параметр сходимости μбольшим, что негативно отразится на способности фильтра противостоять шумам.
Поэтому попробуем разделить задачу фильтрации сигнала с ФМн-2 на две: подстройка амплитуды и фазы несущей частоты и подстройка фазы сигнала, передающей информацию. Решать эти задачи будем, используя два адаптивных фильтра, при этом, для уменьшения ошибки, связанной с появлением и суммарной, и разностной частот при перемножении синусоид, будем рассматривать комплексный сигнал, описываемый выражением:
где 
- амплитуда несущей частоты, 
- фаза несущей частоты, 
- формационная составляющая фазы. Настраиваемые коэффициенты первого фильтра обозначим 
, во втором - 
.
Для формирования сигнала первого фильтра воспользуемся известной «схемой Пистолькорса» [4], получившей широкое применение в широкополосных системах (например, [5]). В соответствии со схемой Пистолькорса, если возвести входной сигнал в квадрат, получим:
где 
-шум.
Т.к. 
принимает значения 
, 
примет значения ,
т.е. после умножения получим сигнал с частотой и фазой, равный удвоенным частоте и фазе несущего колебания. Подав сигнал 
на вход адаптивного фильтра и установив величину 
, получим значения подстроечных коэффициентов 
для частоты 
, которые после преобразования дадут значения подстройки амплитуды и фазы несущего колебания. Эти значения будем использовать при генерации эталона во втором таком же фильтре.
Теперь фаза и амплитуда эталона во втором фильтре совпадают с фазой и амплитудой несущей частоты, поэтому настройка коэффициентов 
должна обеспечить переключение фазы выходного сигнала второго фильтра с 0 на π в соответствующие моменты, а это значит, что коэффициент μ можно выбрать достаточно большой. Схема системы представлена на рисунке 4.
Для преобразования коэффициентов 
используются блоки LUT (LookupTable). На выходе 1 модели наблюдается очищенный модулированный сигнал на несущей частоте. На выходе 2 - фаза этого сигнала или, что эквивалентно, информационная составляющая фазы сигнала 
- 
.
Принцип работы фильтра состоит в следующем. Разность 
между сигналом удвоенной частоты 
и его моделью 
, пропорциональная разности фаз и амплитуд этих сигналов, гетеродинируется на нулевую частоту с помощью эталонного генератора (для получения «отрицательной» частоты используется блок комплексного сопряжения). Сигнал нулевой частоты представляет собой мгновенную разность фаз 
и 
. Далее умноженное на коэффициент 
значение накапливается в интеграторе (выполняет тут и функцию фильтра) в виде настраиваемых коэффициентов 
, стремящихся к истинному значению разности фаз и амплитуд сигналов 
и 
. За счет малого 
получаем узкую полосу пропускания фильтра, достаточную для прохождения синусоидального сигнала.
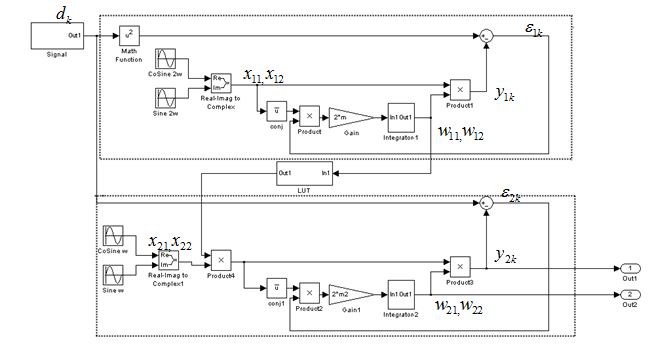
Рисунок 4 - схема двойного фильтра в Simulink
Значения w11,w12 преобразуются с помощью таблицы и служат для поворота фазы эталонного генератора во втором фильтре. Таким образом, фаза и амплитуда несущей частоты сигнала 
оказываются согласованными с фазой и амплитудой эталонного генератора во втором фильтре. Разность 
между сигналом 
и его моделью 
, пропорциональная разности фаз и амплитуд этих сигналов, гетеродинируется на нулевую частоту с помощью эталонного генератора (для получения «отрицательной» частоты используется блок комплексного сопряжения). Сигнал нулевой частоты пропорционален мгновенной разности фаз 
и 
, которая может быть равна или 0, или π. Далее умноженное на коэффициент 
значение накапливается в интеграторе в виде настраиваемых коэффициентов 
, стремящихся к истинному значению разности фаз и амплитуд сигналов 
и 
. За счет большого 
получаем широкую частоту пропускания фильтра.
Выход фильтра (значения w21,w22) и исходный сигнал показаны на рисунке 5.
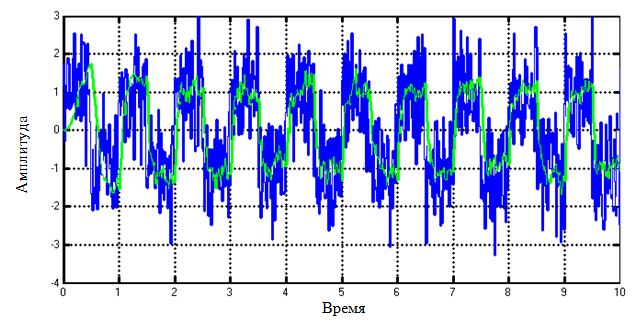
Рисунок 5 - результат работы фильтра
Более светлой линией на рисунке 5 показан выход фильтра. Видно, что шумы значительно упали, а информационная часть фазы сигнала восстановлена, несмотря на случайное значение фазы несущей частоты.
Таким образом, благодаря использованию адаптивного цифрового фильтра с малым значением коэффициента адаптации , настроенного на удвоенную несущую частоту, удалось достаточно точно судить о фазе и амплитуде несущей частоты сигнала, сократив тем самым неопределенность при детектировании сигнала. Настраиваемые весовые коэффициенты второго фильтра (при использовании ФМн-2) будут представлять собой зашумленную информационную составляющую фазы сигнала. Второй фильтр может быть модифицирован за счет замены дискретного интегратора на другое звено, что, возможно, улучшит характеристики быстродействия и точности рассмотренной модели (см., например, [3]).
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы» (Государственный контракт № 14.740.11.1148 от 09.06.2011).
Рецензенты:
- Куприянов М.С., д.т.н., профессор кафедры ВТФГБОУ ВПО «Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
- Герасимов И.В., д.т.н., профессор кафедры САПР ФГБОУ ВПО «Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.