Рассмотрим особенности протекания процесса проскальзывания при совмещенной обработке резанием и ППД роликами, когда обкатник осуществляет, кроме собственно ППД, еще и приводные функции для обеспечения процесса резания [1]. Таким образом, в рассматриваемом случае второй функцией обкатника будет являться фрикционное взаимодействие с обрабатываемой деталью, свойственное фрикционной передаче, а следовательно, должна существовать взаимосвязь передаваемого обкатником крутящего момента, скоростных параметров и проскальзывания в контакте. В связи с этим определение зависимости проскальзывания от конструктивно-технологических параметров обработки является одной из задач по обеспечению необходимых качества и производительности совмещенной обработки с самоподачей.

Рис. 1. Вмятина со следами рисок от предыдущей обработки на заготовке из стали 20, полученная при вдавливании шарика диаметром 10 мм с усилием 30 кН на прессе Бринелля.
При проскальзывании возникает сила трения, направленная в сторону вращения детали. Поэтому мощность обкатывания необходимо определять с учетом возникающих сил трения в контакте. Наличие проскальзывания объясняется перекрещивающимися осями вращения и изменением диаметров ролика и детали по длине контакта. Первая причина вызвана необходимостью установки ролика на угол внедрения и угол самозатягивания, а вторая обусловлена выпуклостью рабочей поверхности ролика и внедрением его в обрабатываемую деталь. Это приводит к тому, что в каждой точке контакта окружные скорости ролика и детали различны по величине и направлению. Вектор разности этих скоростей есть скорость проскальзывания.
Вопросам исследования проскальзывания в литературе применительно к упруго-пластическому деформированию уделяется мало внимания. Основные результаты получены при упругом перекатывании тел вращения.
Фрикционное взаимодействие деформирующего ролика с обрабатываемой деталью в первом приближении может быть рассмотрено с позиций его подобия фрикционной передаче коническими катками. В плоскости, проходящей через ось вращения ролика, в очаге контакта различают две зоны: внедрения и сбега ролика [2; 5]. Длина зоны внедрения при глубинах внедрения ролика свыше 0,05 мм составляет не более 5% от длины зоны сбега, поэтому, упрощая задачу, этой зоной можно пренебречь, а рассматривать лишь зону выхода ролика из заготовки. Известно, что во фрикционных передачах коническими катками только в случае совпадения вершин конусов катков (О1 и О2 на рис. 2) не будет проскальзывания по всей линии контакта [3]. Для фрикционного контакта деформирующего ролика с деталью получено выражение:
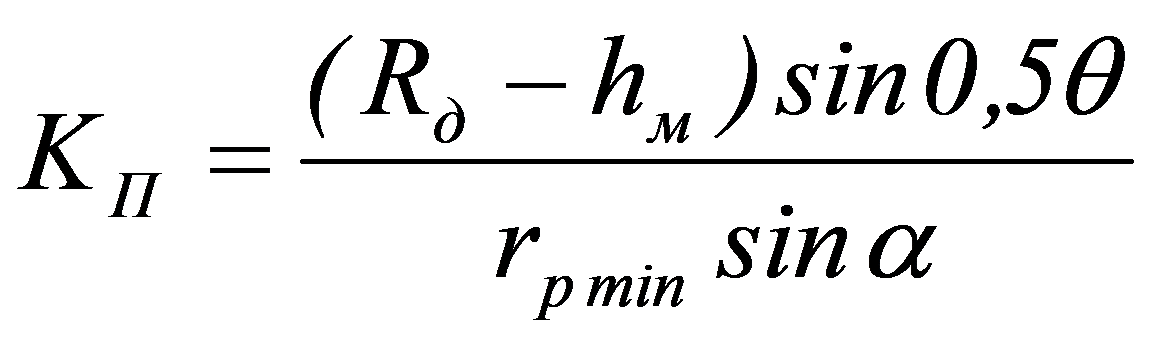 , (1)
, (1)
где Кп - коэффициент проскальзывания; Rд - радиус детали; hм - наибольшая глубина внедрения ролика; θ - угол конуса деформирующего ролика; rpmin - радиус меньшего основания ролика; α - угол образующей контактной зоны (задний угол внедрения ролика).
При значении коэффициента проскальзывания (1), равном единице, проскальзывания не будет по всей линии контакта.
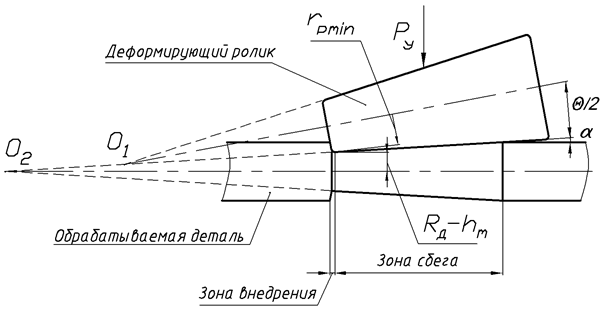
Рис. 2. Схема представления процесса обкатывания как фрикционной передачи коническими катками.
В противном случае отсутствие скольжения будет наблюдаться только в одной точке, радиусы которой на детали и ролике определяются в соответствии с принятыми обозначениями исходя из [3] по формулам:
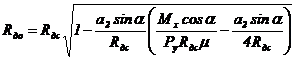 ; (2)
; (2)
![]() , (3)
, (3)
где Rдс - радиус детали в средней точки контакта (рис. 3), определяемый по формуле (4); a2 - длина контакта в зоне сбега; Pу - радиальное усилие прижатия ролика к детали (рис. 2); μ - коэффициент трения скольжения; Mx - крутящий момент на детали.
![]() ,(4)
,(4)
Численный анализ формулы (3) показывает, что при передаваемом крутящем моменте, равном нулю, точка без проскальзывания находится примерно в середине контакта. При возрастании крутящего момента место расположения этой точки меняется - она перемещается или в глубь контакта (при Кп>1) или к точке выхода ролика из контакта (при Кп<1). Последний случай будет соответствовать применению стержневых цилиндрических роликов.
Радиус детали и ролика в произвольной точке контакта К в зависимости от координат точки lк и zк определится по формулам:
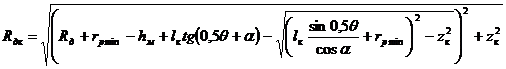 (5)
(5)
![]() (6)
(6)
Окружная скорость детали и ролика в произвольной точке контакта К с учетом формул (2, 3, 5, 6):
![]() ;
; ![]() , (7)
, (7)
где n - частота вращения деформирующего ролика.
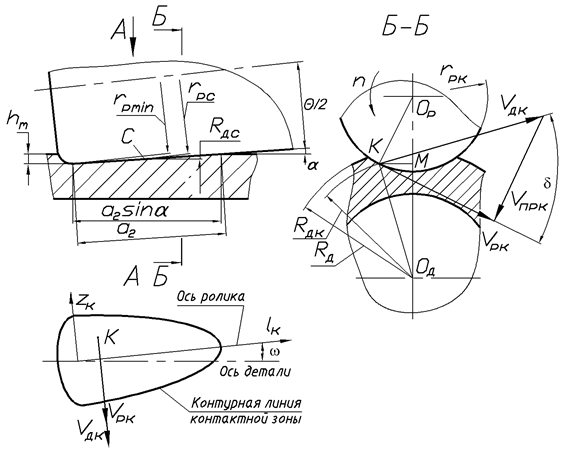
Рис. 3. Схема фрикционного контакта деформирующего ролика с обрабатываемой деталью.
Разность скоростей ролика и детали в произвольной точке контакта определяется по формуле:
![]() , (8)
, (8)
где δ - угол между векторами скоростей ролика и детали в произвольной точке контакта, определяемый по формуле:
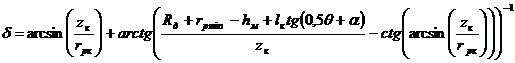 . (9)
. (9)
Опережение или запаздывание ролика относительно детали определяется по знаку проекции скорости проскальзывания на ось zк:
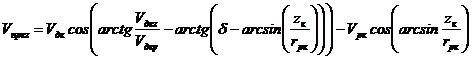 , (10)
, (10)
где Vдкz - окружная скорость точки К; Vдкy - скорость точки К в радиальном направлении, определяемые по формулам:
![]() (11)
(11)
![]() ;
; ![]() . (12)
. (12)
В точках, находящихся на радиусе большем, чем радиус нескользящей точки, деталь запаздывает по сравнению с соответствующими точками ролика, контактирующими с ними, а на меньших радиусах опережает. Это объясняется большей величиной конусности ролика, чем задний угол его внедрения в заготовку.
Мощность, затрачиваемая на проскальзывание в очаге контакта, может быть определена исходя из полученного закона изменения скорости проскальзывания по поверхности контакта Vпрк (8) и закона распределения контактных напряжений σ(lк,zк) [4]. При передаче обрабатываемой заготовке максимального крутящего момента, при условии наличия в контакте точки, в которой скорости ролика и детали равны по значению и имеют одно направление, потери мощности на проскальзывание в зоне сбега определятся из выражения:
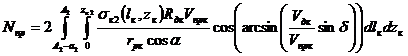 . (13)
. (13)
Мощность, затрачиваемая на деформирование металла, определена также исходя из принятого закона распределения контактных напряжений и скорости движения точек деформируемого металла:
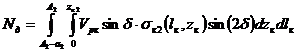 .(14)
.(14)
Как показывают расчеты, потери на проскальзывание составляют менее 1% от общих затрат мощности на обработку ППД и поэтому в практических расчетах могут не учитываться.
Рецензенты:
- Гордеев Борис Александрович, д.т.н., профессор кафедры математики, Нижегородский государственный архитектурно-строительный университет, г. Нижний Новгород.
- Бочкарев Петр Юрьевич, д.т.н., профессор, заведующий кафедрой «Проектирование технических и технологических комплексов», Саратовский государственный технический университет, г. Саратов.



