Основной задачей при алгоритмизации выбора варианта на множестве альтернатив W в случае взаимодействия виртуального эксперта с одним реальным, либо Wg в случае взаимодействия с коллективом экспертов, является формирование матричной игры [1, 3, 4], где альтернативы Wl Є W либо Wl Є Wg рассматриваются как стратегии первого игрока по выдвижению с его точки зрения эффективных вариантов для выбора решения, а оценки эффективности Wl , 
по каждому критерию Ψi , 
как возможности реализации экспертных функций вторым игроком: либо привлечь реального эксперта и получить субъективную оценку δil , , 
(стратегия B1), либо привлечь виртуального эксперта и получить субъективную оценку εil , , (стратегия B2) [1].
В результате имеем (2 x γ) матричную игру. Матрицы такой игры (2 x γ) для критериев Ψi , имеет вид [3]:
|
B W |
B1 |
B2 |
|
W1 |
|
|
|
... |
... |
... |
|
WL |
|
|
Игры вида (2 x L) 
имеют оптимальную стратегию, основанную на сведении к игре (2 x 2) [4],
|
B A |
B1 |
B2 |
|
W1 |
δ1 |
ε1 |
|
W2 |
δ2 |
ε2 |
где W1, W2 - стратегии первого игрока после сведения к игре (2 x 2).
Для матрицы (2 x 2) оптимальные вероятности чистых стратегий вычисляются по формуле [4]:
.
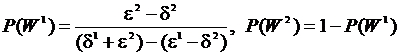Оптимальной является смешанная стратегия, состоящая в случайном применении с вероятностями P(W1) и P(W2) чистых стратегий W1 и W2.
Переход от игры (2 x L) к игре (2 x 2) предлагается осуществлять следующим образом [5]:
1. Исключить из матриц (2 x L) стратегии Wl неудовлетворяющие множеству функций ограничений φ.
2. Оставить в матрице только доминирующие стратегии, т. е. те, по которым большая уверенность в эффективности оценок реального и виртуального экспертов.
3. После предварительного сокращения числа чистых стратегий до L1 < L использовать принцип дихотомии: найти по матрицам
|
B W |
B1 |
B2 |
|
W1 |
|
ε1 |
|
W2 |
|
ε2 |
смешанную стратегию 
вычислить:
, .
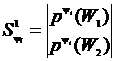Далее определить:
,
,
найти смешанную стратегию 
, по матрицам
|
B W |
B1 |
B2 |
|
|
|
|
|
W3 |
|
|
повторяя этот переход до включения стратегии W1.
В результате получим вероятностные оценки смешанных стратегий для критериев Ψi , :
, ,
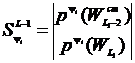на основании которых необходимо осуществить окончательный выбор. Преимущество имеет стратегия с максимальной из 
вероятностью. Если это чистая стратегия, то она принимается за наилучшую чистую стратегию 
. В случае смешанной стратегии сравнивают вероятности, входящие в 
, и продолжают процесс до окончательного выбора чистой стратегии.
Таким образом, имеем I наилучших чистых стратегий по каждому критерию 
. Альтернатива Wl, соответствующая чистой стратегии первого игрока, которая стала наилучшей для наибольшего числа из I (2 x L) матричных игр принимается в качестве согласованного дуального решения 
.
Структурная схема алгоритма дуального режима взаимодействия реального и виртуального экспертов представлена на рис. 1.
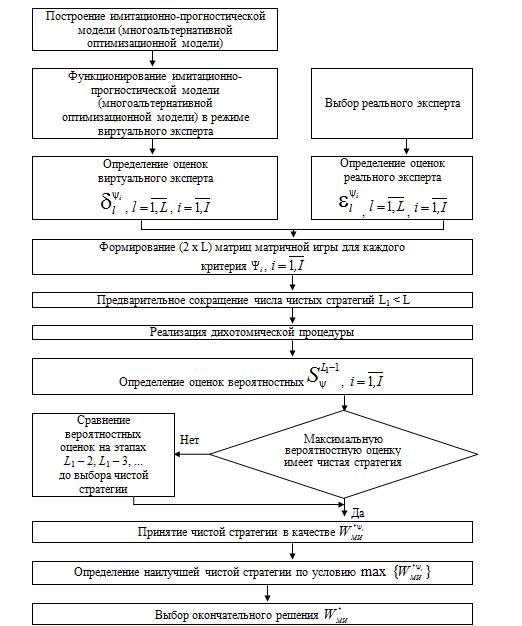
Рисунок 1. Структурная схема алгоритма дуального режима взаимодействия реального и виртуального эксперта
Рецензенты:
- Чопоров О.Н., д.т.н., профессор, заведующий кафедрой технологических и автоматизированных систем электронного машиностроения, ФГБОУ ВПО «Воронежский государственный технический университет», г. Воронеж.
- Драпалюк М.В., д.т.н., профессор, проректор по науке и инновациям, ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.