Задачи формирования инвестиционного портфеля были поставлены в [8], в [10] для их решения применены методы линейной оптимизации. В работах [4; 5] и ряде других сформулированы задачи формирования оптимальных портфелей при различных предположениях, где в качестве целевой функции принимается чистая приведенная (NPV) или накопленная (NFV) стоимость портфеля.
Под (дискретным) инвестиционным проектом (потоком платежей) понимается вектор С = (c0 , c1 , ... , cn), компонента ck которого - это платеж (при ck<0) или возврат средств (при ck>0) в момент времени k [3]. Предположим, что инвестору предложен набор проектов, из которых необходимо выбрать некоторое количество проектов для финансирования. Предполагается, что в качестве альтернативного используется вложение средств с фиксированным годичным коэффициентом накопления. В работе [9] поставлена и проанализирована задача формирования оптимального портфеля инвестиционных проектов, если для некоторых групп проектов предусмотрены групповые платежи. Например, при финансировании хотя бы одного проекта в некотором регионе необходима аренда помещения или приобретение спецтранспорта. В [9] предполагалось, что для групп проектов могут осуществляться только платежи. В то же время в приведенных примерах офис или транспортное средство на некоторое время может сдаваться в аренду, а это приведет и к поступлениям средств.
Будем считать, что сроки выполнения всех проектов совпадают - при необходимости проекты можно дополнить нулевыми платежами. При этом предполагается возможность зависимости между некоторыми проектами, т.е. выбор проекта для включения в портфель зависит от того, включен ли в портфель некоторый другой проект.
Для решения поставленной в [3] задачи применялись точные методы, такие как метод «ветвей и границ» и метод отсечений Гомори [7] в стандартном виде, и были разработаны эвристические алгоритмы - модифицированный метод «ветвей и границ» и эволюционный алгоритм (1+1)-ЕА [2; 3].
Блок-схемы алгоритмов модифицированный метод «ветвей и границ» и эволюционный алгоритм (1+1)-ЕА представлены на рисунках 1 и 2.
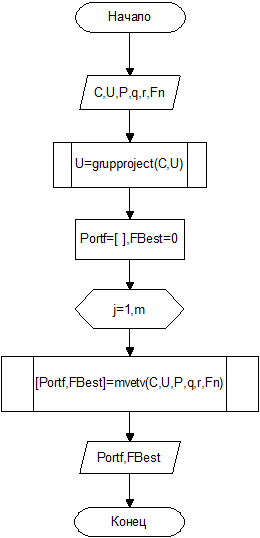
Рисунок 1. Блок-схема модифицированного метода «ветвей и границ»
Основные обозначения (рис. 1): С - множество исходных инвестиционных проектов; U - подмножества проектов; P - множество платежей по группам проектов; q, r - банковские ставки дисконтирования и заимствования; Fn - начальный капитал инвестора; m - длительность проектов; n - количество проектов; s - количество проектов U; Portf - формируемый инвестиционный портфель; FBest - итоговый капитал инвестора; grupproject(C,U) - пользовательская процедура, создающая из всех проектов, не входящих ни в одно подмножество U, дополнительное подмножество U; mvetv(C,U,P,q,r,Fn) - пользовательская процедура, рассчитывающая портфель стандартным методом «ветвей и границ» для каждого подмножества проектов U в отдельности, но с учетом включенных с портфель проектов.
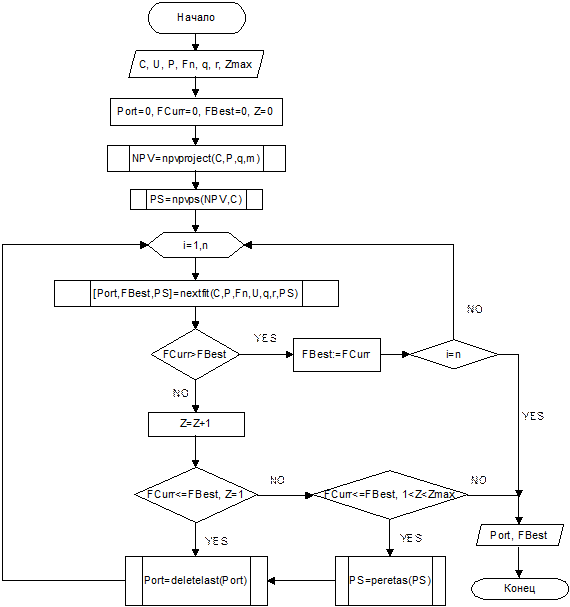
Рис. 2. Блок-схема эволюционного алгоритма (1+1)-ЕА
Основные обозначения (рис. 2): Zmax - максимальное заданное число неудачных включений проектов в портфель (неудача заключается в том, что при включении проекта в портфель результирующий капитал инвестора не увеличивается); Port - текущий портфель проектов; FCurr - текущее значение капитала инвестора; FBest - итоговый капитал инвестора; Z - текущее число неудачных включений проектов в портфель; npvproject(C,P,q,l) - пользовательская функция, рассчитывающая значение чистого приведенного дохода (NPV) проектов по формуле NPV= 
+∑(( 
)/ n), где k - момент времени, в который выполняются платежи по проектам; npvps(NPV,C) - пользовательская процедура, формирующая из исходных проектов приоритетный список PS в порядке убывания их значений NPV; nextfit(C,P,Fn,U,q,r,PS) - пользовательская процедура, которая помещает по порядку проекты из приоритетного списка PS в текущий портфель (при этом из списка PS он удаляется), а также рассчитывается FСurr для этого портфеля по формуле: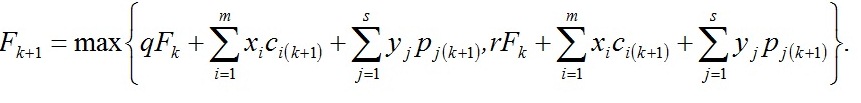 
Peretas(PS) - пользовательская процедура, которая случайным образом переставляет элементы в приоритетном списке PS.
Для анализа эффективности разработанных алгоритмов был создан комплекс программ «Формирование инвестиционного портфеля».
Процесс разработки комплекса программ целесообразно начать с определения набора требований к нему. Весь набор требований разделен на:
- функциональные (описывающие функции комплекса программ);
- к архитектуре и хранилищу данных (как система должна быть построена);
- к средствам разработки (регламентируют используемые для разработки средства, инструменты, серверное ПО и готовые программные модули);
- к разработке эргономичного интерфейса.
Согласно функциональным требованиям, система должна обеспечивать выполнение следующих функций:
- решение задачи формирования оптимального инвестиционного портфеля проектов методом «ветвей и границ» (программа Vetv);
- решение задачи формирования оптимального инвестиционного портфеля проектов методом отсечений Гомори (программа Gomori);
- решение задачи формирования оптимального инвестиционного портфеля проектов модифицированным методом «ветвей и границ» (программа VetvModif);
- решение задачи формирования оптимального инвестиционного портфеля проектов с помощью эволюционного алгоритма типа (1+1)-ЕА (программа Evolut);
- автоматическая генерация списка задач формирования оптимального инвестиционного портфеля проектов (программа Generat);
- открытие задачи из файла и вывод результатов решения задачи для дальнейшего использования инвестором в отдельный файл.
На рисунке 3 представлена функциональная модель процесса формирования оптимального инвестиционного портфеля проектов.
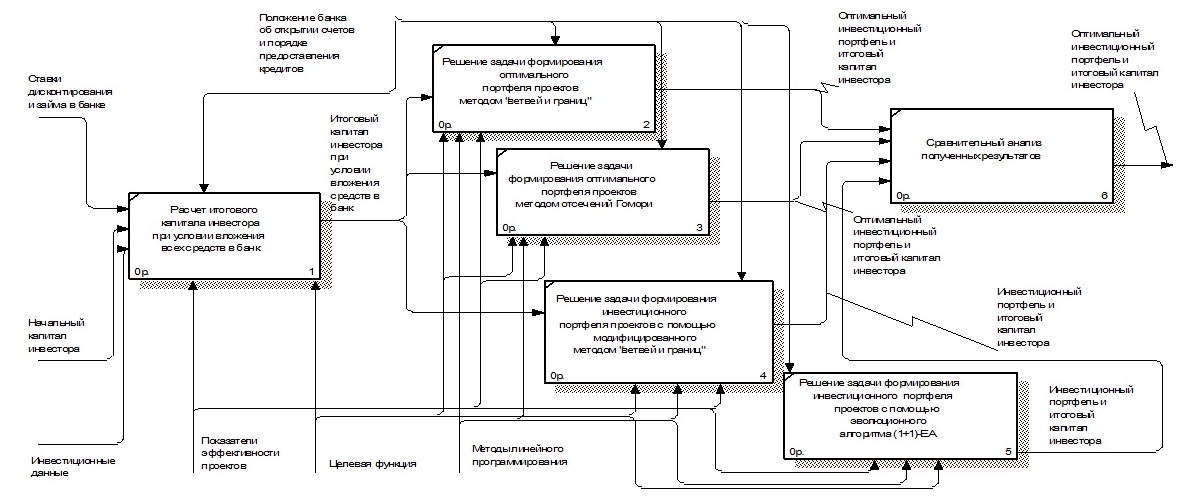
Рис. 3. Функциональная модель процесса формирования оптимального инвестиционного портфеля проектов
В комплекс программ «Формирование инвестиционного портфеля» входят четыре программных модуля Vetv, Gomori, VetvModif, Evolut, реализованных на языке Object Pascal в среде программирования Borland Delpfi 7.0. Программы Vetv, Gomori, VetvModif и Evolut на основании соответствующих оптимизационных алгоритмов и входных данных (начальный капитал инвестора F-1, банковские ставки дисконтирования и займа q и r, длительность проектов, платежи по проектам, число проектов, число и состав подмножеств Uj, платежи по группам проектов Pj, условия зависимости проектов) осуществляют формирование оптимального (Vetv, Gomori) или близкого к оптимальному (VetvModif и Evolut) портфеля инвестиционных проектов, а также расчет чистой будущей стоимости портфеля (NFV) и вывод результатов в файл для дальнейшей работы.
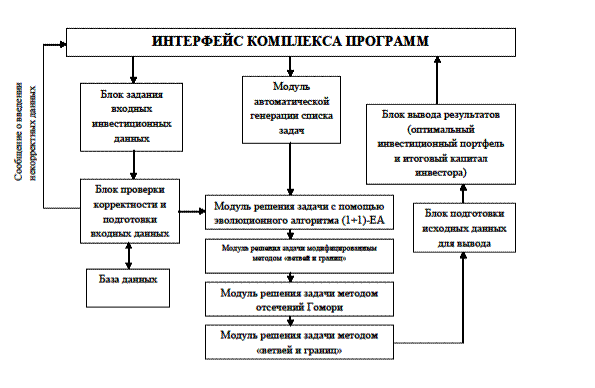
Рис. 4. Архитектура комплекса программ «Формирование инвестиционного портфеля»
На рисунке 4 представлена архитектура разработанного комплекса программ:
- интерфейс комплекса программ - предоставляет пользователю возможность ввода и просмотра исходных данных и результатов работы системы;
- блок задания входных инвестиционных данных - позволяет задавать входные данные, состав которых зависит от выбранного метода решения задачи;
- блок проверки и подготовки данных - производит отсев некорректных данных (выводится соответствующее сообщение пользователю), а также служит для инициализации исходных данных;
- модуль генерации списка задач - случайно генерирует задачи в заданных пользователем диапазонах;
- четыре модуля решения задачи - производят решение оптимизационной задачи соответствующими методами;
- блок подготовки исходных данных - производит инициализацию выходных данных;
- блок вывода результатов - выводит результаты вычислений на экран и сохраняет их во внешних файлах;
- база данных, которая хранит инвестиционную информацию, находится за пределами комплекса программ для повышения надежности и быстроты доступа к данным.
С помощью комплекса программ «Формирование инвестиционного портфеля» был проведен численный эксперимент [7].
Всего было сгенерировано 3000 случайных примеров, результаты решения которых показали эффективность модифицированного метода «ветвей и границ» (отношение конечной стоимости полученного портфеля к стоимости оптимального) - в среднем равна 0,97, эффективность эволюционного алгоритма (1+1)-ЕА при принятых правилах останова в среднем равна 0,88. Для задачи портфельного анализа проведен численный эксперимент, в результате которого установлены тенденции изменения эластичности накопленной стоимости оптимального портфеля к процентным ставкам в зависимости от параметров задачи. Также исследовано влияние на результат числа подмножеств, на которые разбито множество проектов. С ростом числа подмножеств накопленная стоимость оптимального портфеля в среднем падает, причем темп падения уменьшается при увеличении числа проектов [1; 2; 3].
Для возможности формирования оптимального инвестиционного портфеля проектов при наличии групповых затрат и зависимости проектов были разработаны требования к комплексу программ, функциональная модель и архитектура КП, на основании которых разработан комплекс программ «Формирование инвестиционного портфеля». Данный программный комплекс позволяет в полном объеме решать поставленные задачи и может быть адаптирован под конкретные требования инвестиционной политики предприятия.
Рецензенты:
- Спивак С.И., д.ф.-м.н., профессор, зав. кафедрой математического моделирования Башкирского государственного университета Минобрнауки РФ, г. Уфа.
- Юлмухамедов Р.С., д.ф.-м.н., профессор, главный научный сотрудник Института математики с вычислительным центром Уфимского научного центра Российской академии наук, г. Уфа.
Работа получена 30.08.2011