Процессы, происходящие в геотермальных системах (одиночная скважина, геотермальная циркуляционная скважина (ГЦС), многозабойная скважина), столь разнообразны и подвержены влиянию стольких факторов, что их учет, а тем более управление ими при их эксплуатации становится весьма сложной проблемой.
Для принятия эффективных управленческих решений в различных геотермальных системах необходимо иметь надежные методы, позволяющие осуществить выбор наилучшего из возможных вариантов их эксплуатации. В основу таких методов лежат оптимизационные методы, ориентированные на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов.
Одним из важнейших критериев, оценивающих эффективность ГЦС, является критерий минимума удельных капитальных затрат [1]:
![]() , (1)
, (1)
где a1,b1, A1,A2 - постоянные коэффициенты, В - капиталовложения в наземную систему, dH, dД - диаметры нагнетательной и добычной скважин, соответственно, H- глубина скважины, G - дебит добычной скважины.
С учетом эффекта термолифта и гидравлических потерь давления в скважинах и наземном трубопроводе для дебита ГЦС получаем формулу [2]:
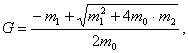
где ![]()
![]()
![]() , а - расстояние между скважинами,
, а - расстояние между скважинами, ![]() - перепад между давлениями на забое нагнетательной скважины и на стенке добычной скважины.
- перепад между давлениями на забое нагнетательной скважины и на стенке добычной скважины.
Очевидно, что эксплуатация ГЦС сопряжена разного рода энергетическими затратами. В первую очередь они связаны с затратами на обратную закачку в пласт отработанной термальной воды (ТВ). Эти затраты, очевидно, зависят от темпов эксплуатации ГЦС, т.е. дебита системы, который в свою очередь зависит от диаметров скважин.
Практическая эксплуатация ГЦС имеет смысл в том случае, когда затраты энергии на обратную закачку составляют лишь относительно небольшую долю общей, получаемой ГЦС энергии.
Через ЕПЛ обозначим долю общей энергии ГЦС, получаемой в результате ее эксплуатации, за вычетом энергии на обратную закачку отработанной воды в пласт:
![]() ,
,
где ![]() , - потери давления в скважинах и в пласте.
, - потери давления в скважинах и в пласте.
Значение оптимального дебита, максимизирующего ЕПЛ определяется формулой:
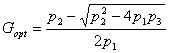 , (2)
, (2)
где ![]() ,
, ![]() ,
, ![]() .
.
В табл. 1 приведены функциональные зависимости оптимального дебита от диаметра скважины, полученные для некоторых месторождений ТВ при =const.
Таблица 1. Функциональные зависимости оптимального дебита от величины диаметра для некоторых месторождений ТВ
|
Кизляр |
Тарки |
Ачису |
Тернаир |
ЮСК |
|
|
|
|
|
|
Таблица 2. Оптимальные параметры ГЦС для некоторых месторождений в зависимости от значений ΔP, полученные при условии минимума F1
|
КИЗЛЯР |
||||||||
|
ΔP, МПа |
G, кг/с |
d, м |
a, м |
ΔPH, МПа |
|
F1, от.ед/Дж |
F2, % |
|
|
1 |
6,6 |
0,124 |
510 |
0,46 |
3,19 |
14 |
99 |
|
|
2 |
9,7 |
0,131 |
619 |
1,2 |
12,3 |
10 |
99 |
|
|
5 |
18,8 |
0,144 |
860 |
3,5 |
68,4 |
5,8 |
98 |
|
|
10 |
33 |
0,157 |
1140 |
7,4 |
253 |
3,7 |
97 |
|
|
МАРТОВСКОЕ - ЮСК |
||||||||
|
ΔP, МПа |
G, кг/с |
d, м |
a, м |
ΔPH, МПа |
|
F1, от.ед/Дж |
F2, % |
|
|
1 |
13,2 |
0,15 |
367 |
0,5 |
6,9 |
8,7 |
99 |
|
|
2 |
18,2 |
0,16 |
431 |
1,28 |
24 |
6,7 |
99 |
|
|
5 |
34 |
0,173 |
590 |
3,66 |
130 |
4 |
98 |
|
|
10 |
58,6 |
0,186 |
774 |
7,7 |
471 |
2,6 |
96 |
|
|
ТЕРНАИР |
||||||||
|
ΔP, МПа |
G, кг/с |
d, м |
a, м |
ΔPH, МПа |
|
F1, от.ед/Дж |
F2, % |
|
|
1 |
17,6 |
0,16 |
599 |
0,61 |
11,2 |
7,2 |
99 |
|
|
2 |
27 |
0,172 |
744 |
1,4 |
40 |
5 |
99 |
|
|
5 |
53,3 |
0,19 |
1044 |
3,85 |
213 |
2,95 |
98 |
|
|
10 |
93 |
0,2 |
1376 |
8 |
773 |
1,9 |
96 |
|
Оценки эффективности сложных систем, каковыми являются и геотермальные системы, не будут объективными только лишь на основе одного, даже очень важного критерия, каким является критерий удельных капитальных затрат. При этом приходится учитывать требования технического, экологического и другого характера. Технические требования находят свое выражение в показателях, связанных с функционированием системы и ее технологических процессов.
Для оценки энергетической эффективности ГЦС определим следующий функционал, показывающий долю общей энергии ГЦС, за вычетом энергии, затрачиваемой на обратную закачку, который необходимо максимизировать:
![]() ; (3)
; (3)
где ![]() - энергия, затрачиваемая на закачку, обратно в пласт обработанной ТВ,
- энергия, затрачиваемая на закачку, обратно в пласт обработанной ТВ, ![]() - энергия, получаемая от теплоносителя массой G(кг/с) в результате изменения его температуры на ΔT(К).
- энергия, получаемая от теплоносителя массой G(кг/с) в результате изменения его температуры на ΔT(К).
Функционал F2, зависит от многих факторов, в том числе и от диаметров dH и dД. В табл. 2 приведены значения критериев F1 и F2 в зависимости от изменяющихся значений депрессии ΔP для некоторых месторождений ТВ.
Анализ данных, полученных в результате численного расчета, показывает, что с возрастанием значений депрессии давления ΔP также растет и энергия закачки EЗАК, причем энергетическая эффективность ГЦС (критерий F2) при этом - уменьшается.
Исследование поведения определенных критериев на зависимость от мощности продуктивного пласта b и от глубины залегания пласта Н показало, что эти факторы влияют на значения критерия F1 практически не влияют на критерий F2.
Основной вывод, вытекающий отсюда, заключается в том, что при создании ГЦС необходимо ориентироваться на такие площади, которые при относительном неглубоком залегании имеют большую мощность продуктивного пласта. А при создании ГЦС на конкретной площади дебит необходимо поддерживать на таком уровне, который обеспечивал бы выполнение поставленных целей.
При освоении геотермальных месторождений помимо оптимизации параметров ГЦС приходится решать и ряд взаимосвязанных задач по определению схемы размещения скважин и их числа.
Рассматривая в качестве схемы размещения скважин на месторождении круговую батарею с расположенной в центре нагнетательной скважиной [1] для определения оптимального дебита такой системы получаем формулу:
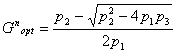 , (4)
, (4)
где ![]() ,
, ![]() ,
, ![]() , n - число добычных скважин в батарее.
, n - число добычных скважин в батарее.
Проведенные расчеты (табл. 3), по оптимизации параметров круговой батареи ( ![]() ) с условием минимума удельных капитальных затрат (1) и значения дебита, полученные на основе формулы (4) при различных количествах добычных скважин n в батарее показали, что рост числа скважин при относительно небольшом увеличении значений критерия F1 (20-40 %) (для значений депрессии ΔP порядка до 10 МПа) позволяет получать значительно большие дебиты (увеличение может составить 50 % и более). Увеличение депрессии ΔP приводит при улучшении оценок по критерию F1 к значительному ухудшению оценок по F2 критерию.
) с условием минимума удельных капитальных затрат (1) и значения дебита, полученные на основе формулы (4) при различных количествах добычных скважин n в батарее показали, что рост числа скважин при относительно небольшом увеличении значений критерия F1 (20-40 %) (для значений депрессии ΔP порядка до 10 МПа) позволяет получать значительно большие дебиты (увеличение может составить 50 % и более). Увеличение депрессии ΔP приводит при улучшении оценок по критерию F1 к значительному ухудшению оценок по F2 критерию.
Поэтому при освоении конкретного месторождения ТВ целесообразно создавать круговые батареи, а решение о количестве добычных скважин в батарее необходимо принимать с учетом реальных потребностей потребителей в тепловой энергии. При высоких значениях депрессии увеличение числа добычных скважин в батарее резко ухудшает оценки по второму критерию F2. Поэтому решение о числе скважин в батарее необходимо принимать с учетом оценок по обоим критериям.
Таблица 3. Оптимальные параметры круговой батареи при различных значениях количества добычных скважин в батарее
|
ΔP =1 МПа |
||||||||
|
n |
ΔPH, МПа |
G*, кг/с |
dД, м |
dH, м |
F1, от.ед/Дж |
F2, % |
||
|
1 |
0,96 |
31 |
0,2 |
0,2 |
11,2 |
99 |
||
|
2 |
0,6 |
21,5 |
0,18 |
0,225 |
11,6 |
99 |
||
|
3 |
0,4 |
17 |
0,164 |
0,241 |
12,4 |
99 |
||
|
4 |
0,26 |
14 |
0,153 |
0,254 |
13,2 |
99 |
||
|
5 |
0,15 |
12 |
0,145 |
0,262 |
13,9 |
99 |
||
|
6 |
0,07 |
10,5 |
0,14 |
0,27 |
14,7 |
99 |
||
|
ΔP=10 МПа |
||||||||
|
n |
ΔPH, МПа |
G, кг/с |
dД, м |
dH, м |
F1, от.ед/Дж |
F2, % |
||
|
2 |
8,5 |
83 |
0,21 |
0,263 |
3,98 |
93 |
||
|
3 |
7,7 |
66 |
0,195 |
0,28 |
4,2 |
90 |
||
|
4 |
7,1 |
55 |
0,182 |
0,296 |
4,4 |
88 |
||
|
5 |
6,7 |
47 |
0,173 |
0,3 |
4,6 |
86 |
||
|
6 |
6,3 |
42 |
0,166 |
0,31 |
4,8 |
84 |
||
|
ΔP=50 МПа |
||||||||
|
n |
ΔPH, МПа |
G, кг/с |
dД, м |
dH, м |
F1, от.ед/Дж |
,F2 % |
||
|
2 |
45,4 |
260 |
0,24 |
0,3 |
1,6 |
62 |
||
|
3 |
43 |
208 |
0,22 |
0,315 |
1,66 |
46 |
||
|
4 |
40 |
175 |
0,2 |
0,33 |
1,73 |
31 |
||
|
5 |
39 |
153 |
0,197 |
0,34 |
1,8 |
17 |
||
|
6 |
38,3 |
136 |
0,19 |
0,35 |
1,87 |
4 |
||
G* - обозначает дебит одной эксплуатационной скважины.
Для улучшения технико-экономических показателей геотермальной отрасли, для повышения ее рентабельности и конкурентоспособности по сравнению с традиционными энергетическими отраслями необходимо создавать ГЦС с горизонтальными скважинами [2].
В табл. 4 для месторождения Кизляр приводятся рассчитанные оптимальные параметры ГеоТЭС, построенной на базе ГЦС с горизонтальными скважинами. Увеличение значений диаметра скважин улучшает оценки по критерию , а по критерию существует оптимум, его минимума. Для месторождения Кизляр таким значением диаметра является - 0,26 м. С увеличением диаметра растут и длины горизонтальных стволов добывающей и нагнетательной скважин. Причем длина последней растет значительно быстрее, что объясняется увеличением зоны дренирования, способствующим уменьшению потерь давления и увеличению полезной мощности ГеоТЭС (табл. 4).
При разработке ГМ всегда возникает проблема выбора системы добычи геотермального теплоносителя (одиночная скважина, ГЦС, ГЦС с горизонтальными скважинами, батарея скважин с n - добывающими и одной нагнетательной, многозабойная скважина с n горизонтальными стволами), обеспечивающей при возможно меньшей себестоимости добычи теплоносителя возможно большую энергетическую эффективность с удовлетворением потребностей потребителя.
Таблица 4. Оптимальные параметры ГеоТЭС для ГЦС с горизонтальными скважинами при одной паре скважин в зависимости от диаметра скважины
|
Кизляр |
||||||
|
d, м |
G, кг/с |
a1, м |
a2, м |
Wn МВт |
F1, от.ед/Вт |
F2, % |
|
0,1 |
15 |
18 |
244 |
0,3 |
10,9 |
81 |
|
0,13 |
28,4 |
26 |
338 |
0,63 |
7,35 |
82 |
|
0,15 |
40 |
32 |
404 |
0,9 |
6,13 |
83 |
|
0,17 |
54 |
38 |
474 |
1,2 |
5,35 |
83,4 |
|
0,19 |
70 |
44 |
547 |
1,6 |
4,84 |
84 |
|
0,2 |
78 |
44 |
547 |
1,8 |
4,66 |
84,5 |
|
0,23 |
108 |
59 |
700 |
2,5 |
4,3 |
85,3 |
|
0,26 |
142 |
70 |
824 |
3,3 |
4,16 |
86,2 |
|
0,29 |
180 |
84 |
954 |
4,2 |
4,17 |
87 |
|
0,32 |
222 |
98 |
1092 |
5,3 |
4,3 |
88 |
|
0,35 |
268 |
113 |
1238 |
6,4 |
4,55 |
89 |
|
0,38 |
318 |
129 |
1391 |
7,7 |
4,9 |
90 |
|
0,41 |
370 |
147 |
1552 |
9 |
5,42 |
91 |
Трудность выбора решения в условиях многоцелевой оптимизации определяется не столько количеством критериев оптимизации и тем более вариантов решения, сколько их противоречивостью.
Так, для конкретного месторождения ТВ всегда возникает задача определения оптимальной технологической схемы добычи теплоносителя, удовлетворяющей следующим условиям:
- минимуму удельных капитальных затрат;
- максимуму энергетической эффективности;
- максимуму полезной мощности ГеоТЭС.
Проведенный сравнительный многокритериальный анализ для четырех технологических схем добычи теплоносителя: I - ГЦС с одной добычной и одной нагнетательной горизонтальными скважинами; II - три добычные вертикальные скважины и одна, расположенная в центре, нагнетательная скважина, III - четыре добычные вертикальные скважины и одна, расположенная в центре, нагнетательная скважина, IV- многозабойная скважина с двумя горизонтальными стволами, показал, что ни одна из рассматриваемых технологических схем не имеет доминирующих оценок по всем рассматриваемым критериям, т.е. все они принадлежать множеству Парето.
Приведя оценки по критериям к соизмеримым значениям для каждой из альтернатив, получаем:
А1=(0; 0,8; 1), А2=(0,72; 0,08; 0), А3=(1; 0; 0), А4= (0,66; 1; 0,82).
Если все критерии считать равноценными, то очевидно, что наилучшей будет альтернатива А4. Действительно, последовательно применяя метод t - упорядочения [3] к имеющимся альтернативам получаем: А4= (0,66; 1; 0,82) ![]() А40=(0,66; 0,82; 1)
А40=(0,66; 0,82; 1) ![]() А1=(0; 0,8; 1)
А1=(0; 0,8; 1)![]() A10=(1; 0,8; 0)
A10=(1; 0,8; 0) ![]() А3=(1; 0; 0)
А3=(1; 0; 0)![]() A30=(0,92; 0,08; 0)
A30=(0,92; 0,08; 0) ![]() А2=(0,72; 0,08; 0).
А2=(0,72; 0,08; 0).
Значит, альтернативы ранжируются следующим образом: А4, А1, А3, А2.
Пусть теперь критерии имеют относительную важность в виде цепочки неравенств, например, вида: F1 > F2>F3. Тогда имеем:
А4= (0,66; 1; 0,82) ![]() А40=(0,66; 0,82; 1)
А40=(0,66; 0,82; 1) ![]() А1=(0; 0,8; 1) и
А1=(0; 0,8; 1) и
А3=(1; 0; 0) ![]() A30=(0,92; 0,08; 0)
A30=(0,92; 0,08; 0) ![]() А2=(0,72; 0,08; 0).
А2=(0,72; 0,08; 0).
Для сравнения альтернатив А1 и А3 нужна дополнительная информация об относительной важности критериев F2 и F3. Поэтому основным недостатком рассмотренного метода является его недостаточная «мощность».
Для установления количественной оценки относительной важности критериев воспользуемся методом Саати [3].
Тогда рассматриваемые альтернативы имеют следующие оценки:![]() = 0,488;
= 0,488;![]() = 0,24;
= 0,24; ![]() = 0,27;
= 0,27; ![]() = 0,87, т.е. наилучшими являются альтернативы с горизонтальными скважинами: ГЦС и многозабойная скважина.
= 0,87, т.е. наилучшими являются альтернативы с горизонтальными скважинами: ГЦС и многозабойная скважина.
Для различных площадей оценки эти будут изменяться, но, несомненно, что среди наилучших альтернатив будут альтернативы геотермальных систем с горизонтальными скважинами.
Основной вывод, который можно сделать на основе проведенного анализа заключается в том, что при освоении новых площадей ТВ необходимо ориентироваться на геотермальные системы с горизонтальными скважинами, ибо они имеют интегрированные преимущества перед другими видами геотермальных систем.
СПИСОК ЛИТЕРАТУРЫ:
- Алхасов А.Б., Магомедбеков Х.Г. Перспективы строительства ГеоТЭС на базе среднепотенциальных термальных вод // Геотермия. Геотермальная энергетика - Сб. науч. тр. ИПГ ДНЦ РАН. Махачкала, 1994, - с. 17-35.
- Алхасов А.Б., Джаватов Д.К. Перспективы использования горизонтальных скважин при разработке геотермальных месторождений / Геотермальная теплоэнергетика - Сб. науч. тр. Отдела энергетики и геотермомеханики ИПГ ДНЦ РАН, Махачкала, 2002, - с.35-46.
- Черноруцкий И.Г. Методы принятия решений.- СПб.: БХВ - Петербург, 2005. - 416 с.



