Введение
Внедрение образовательной робототехники в различные элементы образовательной деятельности открывает новые возможности организации учебного процесса в школе. Робототехника в учебном процессе – это междисциплинарные занятия, сочетающие в себе основы проектной деятельности, программирование, математику и физику [1, 2, 3].
Особой тенденцией в развитии современного образования является поиск новых подходов и методов, позволяющих интегрировать элементы инженерно-технического и информационно-технологического образования для обучения учащихся [2, 4]. Соревнования и конкурсы – важный элемент экосистемы образовательной робототехники, играющий существенную роль в мотивации участия детей и целых регионов, распространении знаний и технологий [5, 6].
В настоящее время существует большое количество соревнований по робототехнике. Но, к сожалению, большинство из них нацелено на аудиторию детей, которые уже освоили основы робототехники и способны решать достаточно серьезные задачи и создавать проекты на основании выявленной проблемы, ее анализа и выбора способов ее решения [6, 7, 8].
Целью практически любого соревнования является не только определение победителя как такового, но и понимание, куда движутся технологии, и определение компетенций участников, необходимых для развития перспективных образцов техники, а также их эксплуатации [5].
В Малой компьютерной академии Северо-Восточного федерального университета (МКА СВФУ) ведется системная работа по разработке регламентов робототехнических соревнований для детей различных возрастных групп.
Робототехнические соревнования представляют собой инновационный подход к обучению, позволяющий вовлечь школьников в активную познавательную деятельность [6]. Однако до сих пор недостаточно исследовано, какие именно знания и умения по физике и математике формируются у школьников в процессе подготовки к таким соревнованиям.
Цель исследования –выявление математических и физических компетенций, развиваемых у школьников младшего и среднего звена в процессе подготовки к соревнованиям «Кольцевые гонки».
Материал и методы исследования
За период работы с 2014 года в МКА СВФУ автором было разработано более 10 регламентов робототехнических соревнований различной сложности. Для расширения охвата участников в 2018 году автор разработал регламент нового соревнования «Кольцевые гонки», направленного на развитие навыков в области кинематики, динамики и геометрии. Соревнование постоянно проводится в рамках ежегодного фестиваля спортивной робототехники «РобОТС» МКА СВФУ и целенаправленно совершенствуется с точки зрения доступности, зрелищности и образовательной ценности. Есть разделение на возрастные категории, также разработаны похожие регламенты для шагоходов и для проведения дистанционных турниров.
Ниже представлен регламент робототехнического соревнования «Кольцевые гонки», в рамках которого участники должны запрограммировать робота на прохождение 3 кругов против часовой стрелки вокруг двух цилиндров за минимальное время.
Размеры и компоненты соревновательного поля
1.Соревновательным полем является белый прямоугольник длиной от 140 см до 250 см и шириной от 90 см до 150 см, ограниченный тонкой линией или краями стола (рис. 1).
2.По центру поля на определенном расстоянии друг от друга устанавливаются два металлических цилиндра черного цвета диаметром 66 мм и высотой 116 мм. От каждого цилиндра до края соревновательного поля проведена тонкая линия (рис. 1).
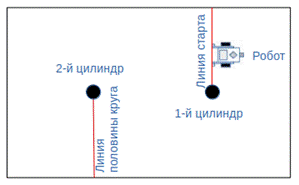
Рис. 1. Схема установки цилиндров и робота на соревновательном поле
Робот
1.Разрешается использовать любой ездящий робот с одним управляющим контроллером, собранный с использованием любых робототехнических наборов и деталей. Запрещено использование клейких, колющих, царапающих деталей.
2. Размеры робота не более 250 мм х 250 мм х 250 мм. Робот не может менять размеры и форму до и после старта.
3.Робот должен быть автономным. Дистанционное управление роботом любым способом ведет к дисквалификации команды.
4.Программа на контроллере должна быть единственной, все посторонние программы удаляются.
5.Запрещено перед стартом вносить любым способом в робота информацию, связанную с расстоянием между цилиндрами. Поэтому запуск программы должен осуществляться одним нажатием единственной запускающей кнопки. В случае контроллера EV3 запускающей кнопкой программы может быть только центральная кнопка «Run». В случае иных робототехнических контроллеров кнопка запуска должна быть заранее отмечена цветным стикером.
Правила проведения состязаний
1.Робот имеет две попытки. В зачет принимается сумма очков за обе попытки. При равенстве очков побеждает команда с меньшей суммой времени выполнения попыток.
2.Продолжительность каждой попытки составляет 120 секунд.
3.Робот устанавливается оператором перед линией старта так, чтобы его проекция не выходила за линию старта. Робот стартует нажатием запускающей кнопки оператором по команде судьи.
4.Расстояние между цилиндрами для каждой попытки определяется жребием.
5.Робот должен проехать 3 круга против движения часовой стрелки вокруг обоих цилиндров, не сбивая цилиндры и не выезжая ни одной опорной точкой за пределы соревновательного поля.
6.Судья фиксирует очки за проезд половины круга. Проездом половины круга считается достижение или полное пересечение проекцией красной линии после объезда дальнего цилиндра против часовой стрелки.
7.Временем выполнения попытки считается зафиксированное время последнего полукруга.
Судья завершает попытку, если:
a.робот проехал 3 круга;
b.закончилось время, отведенное на попытку;
c.цилиндр сбит;
d.опорная точка робота находится за пределами соревновательного поля;
e.участник после старта коснулся робота или цилиндров.
Цилиндр также считается сбитым, если он был сдвинут на 1 см или более.
Очки за каждую половину круга
1.Робот полностью пересек следующую красную линию своей проекцией после объезда цилиндра и не коснулся цилиндра – 5 очков.
2.Робот полностью пересек следующую красную линию своей проекцией после объезда цилиндра и при этом коснулся цилиндра, но не сбил – 4 очка.
3.Робот достиг передней частью следующей красной линии после объезда цилиндра, но не смог полностью пересечь линию своей проекцией – 3 очка.
4.Робот достиг передней частью следующей красной линии после обхода цилиндра и после этого сбил цилиндр – 2 очка.
На основе наблюдений за соревнованиями автором составлены рекомендации по планированию траектории и управлению роботом для достижения лучших результатов.
Для обеспечения максимально прямолинейного движения на некоторых участках требуется подобрать сервомоторы (или коллекторные моторы с энкодерами) с близкими характеристиками. Подбирая моторы, редукторы, колеса и шины, нужно достичь максимальной скорости при сохранении правильной траектории движения. Также для объезда цилиндров, расстояние между которыми заранее не известно, необходимо обнаруживать их датчиком расстояния (ультразвуковым, инфракрасным, лазерным).
Начинающие робототехники при первом знакомстве с соревнованием «Кольцевые гонки» начинают реализовать прямолинейные движения с разворотами на месте на 90 градусов с большим количеством вариантов выполнения (рис. 2).
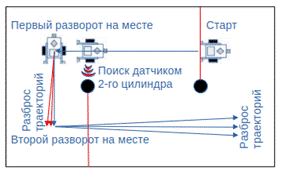
Рис. 2. Очевидная схема планирования траектории обхода двух цилиндров
Но совершить подобным образом три круга вокруг цилиндров очень затруднительно. Главным фактором, негативно влияющим на указанный способ, является наличие у обоих колес люфта (около 5 градусов у большого мотора EV3). Пользуясь моментом, педагог по робототехнике может рассказать детям про редукторы, виды шестеренок, червячную передачу, подшипники качения и скольжения.
Опытные участники соревнований, установив робота на поле, часто тянут его назад на полсантиметра, чтобы избавиться от возможного люфта колес в начале движения. Иначе колесный дифференциальный робот может стартовать в любом из трех направлений (рис. 3):
1) оба колеса находятся с убранным люфтом по направлению движения или оба колеса имеют люфт по направлению движения – робот поедет по синей траектории;
2) люфт левого колеса убран, люфт правого колеса не убран – робот поедет по красной траектории;
3) люфт правого колеса убран, люфт левого колеса не убран – робот поедет по зеленой траектории.

Рис. 3. Варианты траектории при разных состояниях люфта колес на старте
Раскачивание робота при остановке после быстрого разворота на месте заметно на глаз, но и при развороте на низкой скорости нельзя предугадать конечное состояние колес, так как колеса движутся по одному кругу в противоположном друг другу направлении:
1) оба колеса находятся с убранным люфтом по направлению движения– робот поедет по синей траектории;
2) люфт левого колеса убран, люфт правого колес не убран или люфт правого колеса убран, люфт левого колеса не убран – робот поедет по ближней красной траектории;
3) люфт обоих колес не убран – робот поедет по крайней красной траектории.
Соответственно, после каждого разворота на месте количество возможных траекторий увеличивается в 3 раза (рис. 2), что по мере накопления ошибок приведет к выезду за соревновательное поле или к сбиванию цилиндра.
Для повышения точности движения роботов выгоднее заменить два разворота на месте на один поворот по дуге (рис. 4). Этот способ сокращает длину траектории и эффективно устраняет люфты в механизмах. При повороте по дуге оба колеса вращаются в одном направлении, что позволяет постоянно компенсировать небольшие смещения в передаточном механизме. Таким способом обеспечивается более плавное и точное движение робота. Иногда незначительные погрешности, накопленные на первых двух участках трассы, могут привести к некоторому отклонению робота от заданной траектории на последующих участках.
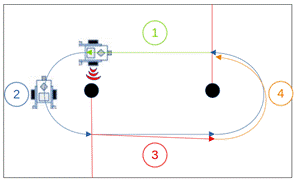
Рис. 4. Оптимальная траектория движения робота
Чаще роботы участников переходят из прямолинейного движения к движению по дуге снижением скорости одного колеса, ближнего к цилиндру. Некоторые, наоборот, для движения по дуге увеличивают скорость внешнего колеса (смотрится очень эффектно), хотя увеличивается риск заноса.
Чтобы реализовать движение робота по дуге необходимого радиуса, следует выполнить точные математические расчеты соотношения скоростей внешнего и внутреннего колес. Далее, посредством программирования двигателей, нужно обеспечить вращение колес по дуге ровно на половину окружности.
Написаны уравнения для расчета отношений между скоростями колес для расчета длины половины окружностей и скоростей, необходимых для движения по дуге за единое время, где h – расстояние между колесами робота (рис. 5):
Sвнеш=2П(Rвнут+h)/2 ; Sвнут=2ПRвнут/2 ; Vвнеш=Sвнеш/t ; Vвнут=Sвнут/t ; откуда получим: Vвнут=VвнешRвнут /(Rвнут+h);
Написаны уравнения для расчета угла a вращения внешнего колеса в градусах, необходимых для преодоления внешней дуги (только половины окружности), где d – диаметр колеса:
Пd/360 = Sвнеш/a ; Пd/360 = П(Rвнут+h)/a; откуда получим: a = (Rвнут+h)*360/d;
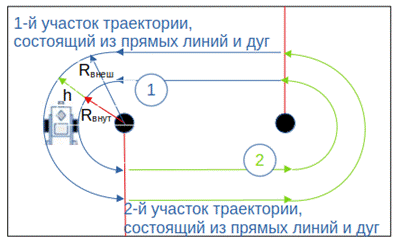
Рис. 5. Траектории движения каждого из двух колес
Результаты исследования и их обсуждение
Тщательный анализ физических процессов и применение математических методов позволяют создать более эффективные алгоритмы управления роботами, что дает существенное преимущество на соревнованиях и имеет важное образовательное значение. Кроме механики, можно изучить со школьниками физическую природу датчиков расстояния.
Предложенные формулы можно запрограммировать и в блочной среде программирования LEGO® MINDSTORMS EV3 (робототехнический конструктор для ребят в возрасте от 10 лет), и в Scratch (визуальный язык программирования для детей), и на других популярных языках программирования роботов.
Для повышения надежности и эффективности управления роботом можно создать одну универсальную функцию для прохождения синего участка трассы под номером 1 в форме крючка (рис. 5). Шестикратный вызов этой функции позволит роботу успешно совершить 3 круга. Измерить расстояние между цилиндрами можно только один раз в начале гонки.
Для участия в соревновании «Кольцевые гонки» достаточно быстро собирается базовая модель «робота-пятиминутки». Настоящая битва разворачивается на этапе программирования и управления, где участники, развивая свои математические и физические компетенции, разрабатывают новые стратегии и соревнуются в скорости и точности прохождения трассы.
Заключение
Анализ результатов соревнований показал, что лучшие результаты демонстрируют команды, применяющие описанные в статье методы оптимизации. Это свидетельствует о том, что такое простое задание, как объезд двух цилиндров, требует довольно глубокого понимания физических процессов и умения применять математические модели. Участники осваивают основы кинематики и динамики, учатся математически рассчитывать траектории движения, оптимизировать алгоритмы управления роботами и учитывать влияние погрешностей в механических системах. Соревнования «Кольцевые гонки» служат эффективным инструментом для формирования и закрепления у школьников начального и среднего звена начальных математических и физических компетенций, способствуют формированию навыков инженерного мышления.



