В современном мире человек сталкивается с переизбытком информации, причем далеко не всегда эта информация достоверная. Ему нужно уметь отличать правду от фейка и вымысла. Способность анализировать информацию, осмысливать, сопоставлять, искать логические связи и объяснения, умение критически мыслить очень важны для современного человека. Перед современной отечественной школой стоит задача подготовить выпускников, умеющих думать, готовых учиться, способных мыслить критически.
Не следует ассоциировать критическое мышление исключительно с выявлением недостатков, отрицательной оценкой любой предлагаемой информации. Умение мыслить критически не означает уметь находить недостатки во всем. Это умение подразумевает способность анализировать информацию, делать логические выводы, аргументировать свою точку зрения [1].
Математике по праву принадлежит особая роль в развитии мышления вообще и критического мышления в частности. Для формирования этих качеств необходимы эффективные методические приемы и средства обучения. Математические задачи – не только важнейшее средство формирования непосредственно математических знаний и умений, но и средство развития умения мыслить. Именно целесообразно подобранные математические задачи представляют собой одно из наиболее эффективных средств развития мышления, формирования такого его качества, как критичность. Практически любая математическая задача в той или иной степени способствует развитию мышления.
Цель данного исследования: обобщить описанные в научно-методических работах и используемые в практике обучения математике типы задач, способствующие развитию критического мышления школьников, выявить типы математических задач, которые наиболее эффективны при формировании критического мышления школьников.
В научных и методических работах в качестве средства формирования критического мышления нередко называют «провоцирующие» задачи (используют также термины «обманные» задачи, «задачи-провокации», «задачи-ловушки»). Провоцирующими называют задачи, формулировка которых провоцирует ученика на ошибку, побуждает к ошибочным действиям. Одна из первых типологий подобных задач представлена в работах М.И. Зайкина [ 2]. Исследователи активно используют выделенные им типы провоцирующих задач: задачи, условия которых навязывают неверный ответ; задачи, условия которых подсказывают неверный путь решения; задачи, в условии которых математические объекты, которые не могут существовать; задачи, вводящие в заблуждение из-за неоднозначности трактовок терминов, выражений [3, 4, 5].
В основном в научно-методических работах приводят примеры провоцирующих задач занимательного характера, однако провоцирующими, т.е. ловушками, могут быть не только занимательные задачи, но и обычные, на первый взгляд не отличающиеся от других учебных задач, предлагаемых на уроке. В частности, примеры подобных задач из курса геометрии приводятся в работах Н.С. Майковой [6]. Следует отметить явную нехватку качественных методических работ, содержащих подборки провоцирующих задач по математике для 7–11-х классов.
Приведем примеры провоцирующих задач, сформулированных на материале школьного курса алгебры и геометрии.
Задачи, условия которых навязывают неверный ответ
Подобные задачи можно найти и в обычных школьных учебниках, чаще всего их можно встретить среди задач, предлагаемых на экзаменах.
Задача. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: 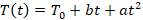 , гдеt− время в минутах,
, гдеt− время в минутах,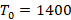 К,
К, 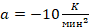 ,
, 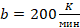 . Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор [7].
. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор [7].
Ловушка в этой задаче заключена в требовании указать наибольшее время. Ученик, решая задачу, определяет, что температура нагревателя равна 1760 К при двух значениях t: 2 и 18. Прочитав слова «наибольшее», ряд учеников ошибочно выбирают 18. Ученики в этом случае не смогли критически оценить ситуацию, проанализировать ее. Они не учли, что через 2 минуты после включения прибор нагреется до 1760 К, и при дальнейшем использовании он может испортиться, поэтому его нужно отключить через 2 минуты.
Для того чтобы обычную задачу превратить в задачу-ловушку, бывает достаточно сформулировать дополнительное требование. Например.
Задача. Решите уравнение 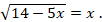 Если уравнение имеет более одного корня, укажите в ответе меньший из корней.
Если уравнение имеет более одного корня, укажите в ответе меньший из корней.
Корнями квадратного уравнения, к которому приводится исходное иррациональное уравнение, являются числа 2 и –7. Однако число –7 не является корнем исходного уравнения. Практика показывает, что требование «указать в ответе меньший из корней» нередко провоцирует ученика на ошибку. Ученик, у которого недостаточно хорошо сформирован навык решения иррациональных уравнений, забывает о необходимости проверить полученные корни или использовать теоремы о равносильных переходах, указывает, что наименьший корень –7. Отсутствие привычки критически оценить свое решение приводит к ошибочному ответу.
Задачи, условия которых навязывают неверный путь решения
Следует заметить, что подобного рода провокации скорее всего приведут к ошибке только ученика, который недостаточно хорошо владеет материалом. Все же стоит признать, что, оказывается, трудно мыслить критически без достаточного количества знаний.
Задача. Сократить дробь 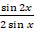 .
.
У ученика, который не усвоил формулу синуса двойного угла, может возникнуть желание просто сократить на 2, а потом еще и на 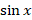 .
.
Задачи про несуществующие объекты
Задача. Дан треугольник АВС, угол С – прямой. СН – высота треугольника, Известны длина высоты СН = 5 см и длина гипотенузы АВ – 8 см. Найдите площадь треугольника.
Подвох: такая геометрическая конфигурация невозможна. Высота прямоугольного треугольника, проведенная из вершины прямого угла, не может быть больше половины гипотенузы.
Среди задач, которые можно отнести к задачам про несуществующие объекты, можно встретить задачи с противоречащими данными. Например.
Задача. В треугольнике АВС АС=5, ВС=8, 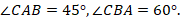 Найти АВ.
Найти АВ.
Ловушка: треугольник, описанный в задаче, не существует, поскольку в треугольнике против большего угла должна лежать большая сторона.
Задачи-ловушки с несуществующими объектами полезно включать в серии однотипных задач. Ученик, несколько раз выполнив похожие операции, нередко теряет бдительность, перестает критически оценивать ситуацию.
Так, например, в серию задач на нахождение площади треугольника по длинам трех сторон можно включить следующую задачу.
Задача. Найти площадь треугольника, длины сторон которого 3, 4 и 7.
Подвох в том, что треугольник с такими длинами сторон не существует, поскольку не выполняется неравенство треугольника.
Приведем пример из алгебры. После изучения формул Виета учитель предлагает ученикам серию задач (уравнений) с требованием: «определите сумму и произведение действительных корней уравнения». Предлагаются уравнения:
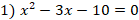 ; 2)
; 2) 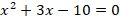 ; 3)
; 3) 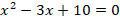 .
.
Используя формулы Виета, ученики быстро отвечают на поставленные вопросы. Ловушка – последнее из этих уравнений, оно не имеет действительных корней. Многие ученики пытаются дать ответ, используя теорему Виета, не удостоверившись, имеет ли уравнение действительные корни.
Большую пользу в плане развития критического мышления несут задачи, имеющие не единственный возможный вариант ответа. Можно привести немало примеров геометрических задач такого типа, например следующие.
Задача. Трапеция с основаниями, длины которых 6 см и 8 см, вписана в окружность, радиус которой равен 5 см. Найдите высоту трапеции.
Задача имеет два ответа, поскольку возможно два разных расположения центра окружности (вне трапеции и внутри нее).
Задача. Около треугольника АВС описана окружность радиусом, равным 2 см. Хорда ВС равна радиусу окружности. Определите градусную меру угла ВАС.
Используя теорему синусов, ученики находят синус угла ВАС, он оказывается равным 0,5. Часть учеников дает один только вариант ответа – 30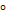 , забывая о том, что такой синус имеет также угол
, забывая о том, что такой синус имеет также угол 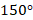 .
.
Так называемые многовариантные планиметрические задачи несколько лет назад активно предлагались на ЕГЭ.
Среди математических задач, способствующих формированию критического мышления, особое место принадлежит задачам на поиск ошибок в представленном решении.
Среди заложенных ошибок могут быть ошибки разного характера:
– содержательные (ошибочно использовано некоторое свойство; не учтены все ограничения; неверно использованы кванторы общности и существования, при аргументации неверно сформулированы определение или теорема, на которую ссылаются, отсутствует обоснование у утверждения; решение проводится только для частного случая и др.);
– логические (используются некорректно причинно-следственные связи, путаница в понятиях «объединение» и «пересечение», неполнота индукции и т.д.);
– вычислительные;
– ошибки в использовании символики;
– графические;
– грамматические [8].
Большая часть методических работ, в которых предлагают задания на поиск ошибок в решении, содержат задания, в которых ученик осознает присутствие ошибки в рассуждениях, поскольку доказано утверждение, противоречащее здравому смыслу [8].
Например, при нахождении площади фигуры в ответе указано отрицательное число; большинство учеников понимают, что в решении допущена ошибка, поскольку площадь не может выражаться отрицательным числом.
Гораздо более сильно развитое критическое мышление требуется при нахождении скрытых ошибок. Целесообразно в качестве преднамеренных ошибок использовать типичные ошибки школьников [9]. Приведем несколько примеров.
Задание. Проверить правильность представленного решения (рис. 1).
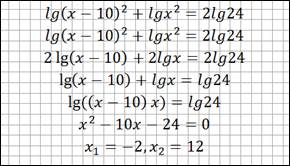
Рис. 1. Решение логарифмического уравнения из ученической тетради
Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного. 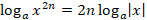 .
.
Задание. Найдите ошибку в решении уравнения (рис. 2).

Рис. 2. Решение иррационального уравнения из тетради ученика
Решение не верно: при возведении в квадрат обеих частей уравнения 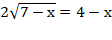 нарушается равносильность, поэтому требуется еще проверка корней (или следует учесть, что выражение, стоящее в правой части, – неотрицательное). В резульате придем к выводу, что число 6 – посторонний корень.
нарушается равносильность, поэтому требуется еще проверка корней (или следует учесть, что выражение, стоящее в правой части, – неотрицательное). В резульате придем к выводу, что число 6 – посторонний корень.
Задание. Установите, правильно ли решено уравнение (рис. 3)?
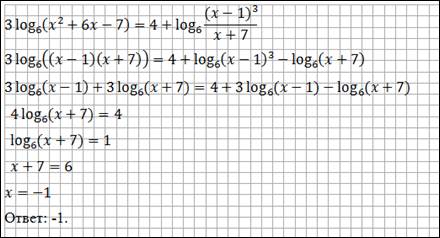
Рис. 3. Решение логарифмического уравнения из ученической тетради
При решении уравнения (рис. 3) допущено сразу несколько ошибок:
1) неправильно применены свойства логарифмов (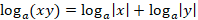 ,
, 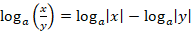 ), в результате произошли сужение области допустимых значений переменной и потеря корней;
), в результате произошли сужение области допустимых значений переменной и потеря корней;
2) не учтена область допустимых значений, полученный корень является посторонним.
Задание. Проверить правильность представленного решения (рис. 4).
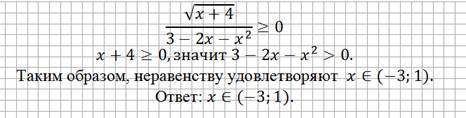
Рис. 4. Решение логарифмического уравнения из ученической тетради
Неравенство решено не верно, потеряно одно решение. Выражение, стоящее в числителе, равно 0 при 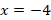 , при этом значении х знаменатель не обращается в ноль, таким образом, оно является решением неравенства.
, при этом значении х знаменатель не обращается в ноль, таким образом, оно является решением неравенства.
В очередной раз приведенные примеры подтверждают тезис о том, что для того, чтобы уметь мыслить критически, все же не всегда достаточно только владения приемами мышления, необходимо иметь и качественные знания.
Заметим, что, предлагая ученикам задание «проверить, верно ли решение задачи», не следует ограничиваться заданиями, при решении которых действительно были допущены ошибки. Периодически следует предлагать и правильно решенные задачи.
Умение критически мыслить подразумевает умение наблюдать, подмечать закономерности, внимательно относиться к деталям. Для формирования этих умений также полезны задачи на поиск закономерностей.
Выводы. Проведенный анализ научных статей и методических разработок, а также собственный многолетний опыт преподавания математических дисциплин позволили выделить типы математических задач, способствующих развитию критического мышления школьников. Проведенное автором исследование показало, что в плане формирования критического мышления наиболее эффективно применение при обучении школьников следующих типов задач: провоцирующих задач про несуществующие объекты; провоцирующих задач, условия которых навязывают неверный ответ или действия; задач на поиск ошибок в предложенном решении.
Эффективность применения перечисленных выше типов подтверждена экспериментально: задачи систематически использовались автором в практике обучения школьников на протяжении десяти лет, целенаправленно систематически проводились диагностика и анализ результатов обучения. Исследование показало, что систематическое использование подобных типов задач при обучении школьников способствует выработке у них навыка внимательно изучать условие задачи, не пренебрегать этапом анализа полученного ответа, критически оценивать каждое выполненное при решении задачи действие, т.е. способствует формированию критического мышления.



