Образовательный процесс должен чутко реагировать на общественные явления, чтобы подготовить специалистов, которые владеют компетенциями, актуальными в быстро меняющемся мире. Одной из целей Государственной программы Российской Федерации «Развитие образования» [1] является «формирование эффективной системы выявления, поддержки и развития способностей и талантов у детей и молодежи, основанной на принципах справедливости, всеобщности и направленной на самоопределение и профессиональную ориентацию всех обучающихся». Для достижения этой цели необходимо не только в школе, но и в вузе использовать инновационные методики обучения и контроля знаний, которые способствуют развитию благоприятных условий для профессионального роста и проявления творческого потенциала студентов.
Одной из таких методик является система укрупнения дидактических единиц (УДЕ). Разработанная еще в прошлом веке доктором педагогических наук, профессором, академиком РАО П.М. Эрдниевым для школьной математики с первого по выпускной классы, она содержит ряд обучающих приемов, таких как «единство составления и решения задач», «совместное изучение взаимосвязанных действий» и другие, которые позволяют совершенно по-другому взглянуть на образовательный процесс, привлекая в него элементы креатива и творчества. По оценкам автора технологии УДЕ, при ее применении сокращается время на изучение различных разделов математики и значительно возрастает качество усвоения учебного материала. Этой тематике посвящено большое число статей и методических разработок, проводятся научные конференции, в которых докладчики демонстрируют применение методики УДЕ на различных уроках в школе (например, [2]). Авторы работы [3] подробно разбирают возможности внедрения данной системы в дисциплину «Математика» средней школы и предлагают с помощью системы УДЕ ввести в высшую школу общий предмет «Линейная математика», в котором сочетались бы линейная алгебра и аналитическая геометрия.
Современные образовательные стандарты для направлений бакалавриата не регламентируют количество зачетных единиц, отводимых на изучение математики, что приводит к существенным различиям в программах разных вузов для одних и тех же направлений. Однако существует ряд основных вопросов, которые необходимо знать студенту вуза. Перечень вопросов определяется направлением подготовки и для студентов физико-математических специальностей – он наиболее широкий. Учитывая значимость фундаментальной математической подготовки этих студентов и ограниченность дисциплин по времени, необходимо использовать новые технологии преподавания высшей математики.
В последние несколько десятков лет стали появляться научные работы, в которых авторы предлагают применять альтернативные образовательные методики при обучении математике в вузе. Так, в работе [4] автор рассматривает сочетание сразу двух методик: педагогики сотрудничества и укрупнения дидактических единиц. «Педагогика сотрудничества» формирует связанные пары, такие как теория – практические приложения, наука – методика обучения, индивидуальная и групповая деятельность и др. В указанной статье эта технология реализована на зачетном занятии по одному из разделов математического анализа, подробно описан весь ход занятия с указанием на особенности применения вышеуказанного методического приема. Отдельно в этой научной работе рассмотрены задачи по аналитической геометрии, в которых реализован принцип укрупнения дидактических единиц. Эта технология относится к формированию внутренней структуры курса, помогает выстроить последовательность изложения материала и решения тех или иных задач. Так, в работах [5, 6] рассматриваются различные понятия теории вероятностей и математической статистики, которые затем иллюстрируются примерами. Широкое применение технологии УДЕ обусловлено самой природой мышления человека. Здесь реализованы общелогические методы научного познания (анализ и синтез, индукция и дедукция, моделирование и др.) на более высоком «знаковом» (или «символьном») уровне восприятия. Это позволяет по-новому взглянуть на сам процесс обучения – сделать его более эффективным, внедряя «деятельности подход». Например, в статье [7] подробно разбирается методика решения задачи из аналитической геометрии в контексте УДЕ, где в качестве дидактической единицы рассматривается действие. Автор предлагает продолжить работу с задачей и после получения ответа – предложить студентам самим сформулировать более общую задачу на базе уже решенной, постепенно ее укрупняя.
Цель исследования заключается во внедрении элементов системы УДЕ при изучении векторного и тензорного анализа студентами профильных (физико-математических) направлений. В основу изложения теоретического материала закладываются блочные структуры определений и свойств. Проблематика практических занятий структурируется по типу и уровню задач.
Материал и методы исследования
Студенты физико-математических направлений вузов должны свободно ориентироваться в многообразии математических абстракций, описывающих реальные объекты. Именно связь с природным объектом делает математическую модель значимой, помогая обучающимся увидеть логику выражений и символов. В школе учащиеся сталкиваются лишь со скалярными и векторными величинами, при этом акцентируется связь между ними: так, вектор может быть записан через его скалярные компоненты или проекции на указанный набор базисных векторов (чаще единичных). В курсе математики высшей школы появляется новый математический оператор – тензор, вводятся первые тензорные величины в физике (тензор инерции, тензор напряжений).
Важно понимать, что термин «тензор» – это общее математическое описание геометрических объектов, которые имеют величину и любое количество направлений. Тензор порядка p имеет содержимое из p направлений и имеет Np компонентов. Таким образом, скаляр – это тензор нулевого порядка, вектор – тензор первого порядка, матрица – тензор второго порядка и т.д.
Хотя любой тензор второго порядка 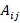 может быть интерпретирован как квадратная матрица, не все квадратные матрицы являются тензорами. Матрицы представляют собой простые массивы произвольных элементов, в то время как тензоры содержат геометрическую информацию о направлении, удовлетворяют законам преобразования для изменения базиса и обладают инвариантными свойствами, независимыми от базиса. Иногда бывает полезно ввести поворот векторного базиса и координат в другую ориентацию. Компоненты и координаты тензора удовлетворяют законам линейного преобразования, которые определяют координаты и компоненты в одном базисе в терминах известных компонентов в другом базисе.
может быть интерпретирован как квадратная матрица, не все квадратные матрицы являются тензорами. Матрицы представляют собой простые массивы произвольных элементов, в то время как тензоры содержат геометрическую информацию о направлении, удовлетворяют законам преобразования для изменения базиса и обладают инвариантными свойствами, независимыми от базиса. Иногда бывает полезно ввести поворот векторного базиса и координат в другую ориентацию. Компоненты и координаты тензора удовлетворяют законам линейного преобразования, которые определяют координаты и компоненты в одном базисе в терминах известных компонентов в другом базисе.
Векторные и тензорные поля также требуют локального базиса в каждой точке для определения векторных/тензорных компонентов. Надо отметить, что обычно используется ортонормированный базис со стандартным обозначением единичных векторов – в декартовой системе координат 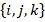 . В вузовском курсе математики на профильных (физико-математических) направлениях студенты переходят к компактной математической записи и от «буквенных обозначений» – к индексной. Введение таких обозначений значительно упрощает не только вид выражений, но и операции с ними. Например, произведение векторов легко записать с помощью специальных символов: Леви-Чевиты –
. В вузовском курсе математики на профильных (физико-математических) направлениях студенты переходят к компактной математической записи и от «буквенных обозначений» – к индексной. Введение таких обозначений значительно упрощает не только вид выражений, но и операции с ними. Например, произведение векторов легко записать с помощью специальных символов: Леви-Чевиты – 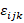 и Кронекера –
и Кронекера – 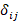 . Так, в ортонормированном базисе (
. Так, в ортонормированном базисе (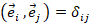 ), вектор
), вектор 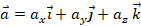 , если
, если 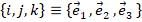 , можно разложить как
, можно разложить как 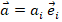 (с учетом правила о повторяющемся в одночлене индексе, по которому ведется суммирование) [8]. Аналогично вводим определение тензора второго порядка:
(с учетом правила о повторяющемся в одночлене индексе, по которому ведется суммирование) [8]. Аналогично вводим определение тензора второго порядка: 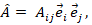 здесь
здесь 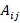 можно интерпретировать как матрицу тензорных компонент.
можно интерпретировать как матрицу тензорных компонент.
Учитывая важность тензорного анализа для физики, можно ввести понятие тензора (табл. 1) и его основные свойства уже в курсе линейной алгебры после изучения матричного исчисления, в рамках технологии укрупнения дидактических единиц. Такое одновременное изучение помогает не только сократить время, затрачиваемое на лекционный материал, освобождая его на решение конкретных примеров и задач, но и показать общность понятий, формируя логику математического мышления будущих специалистов.
Таблица 1
Одновременное введение понятий тензора нулевого, первого и второго рангов
|
Скаляр (тензор нулевого ранга) |
Рис. 1а |
|
|
Вектор (тензор первого ранга) |
Рис. 1б |
|
|
Тензор второго ранга
|
Рис. 1в |
|
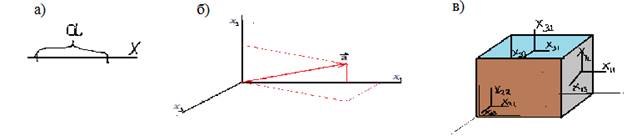
Рис. 1. Графическое представление тензорных величин различного ранга
Далее принцип УДЕ – совместного изучения этих величин – можно распространить на свойства произведения этих величин, которые для наглядности представим в таблице 2.
Таблица 2
Блочное представление произведений тензоров 1-го и 2-го рангов
|
|
вектор |
Тензор 2-го ранга |
|
скаляр |
|
|
|
Вектор |
|
|
|
Вектор
|
|
|
|
Тензор 2-го ранга
|
|
|
После этого предлагается рассмотреть задачи на использование этих свойств (например, [9]), при решении которых внимание студентов акцентируется на аналогиях в задачах, тем самым устанавливаются логические связи в изучаемом материале. Так, предлагается одновременно решить задачи.
Пример 1. Пусть в некоторой декартовой системе координат K известны компоненты вектора 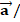 тензора второго ранга
тензора второго ранга 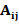 . В системе K′, полученной из K поворотом на некоторый угол вокруг оси z, найти компоненты этого вектора/тензора.
. В системе K′, полученной из K поворотом на некоторый угол вокруг оси z, найти компоненты этого вектора/тензора.
Пример 2. Найти собственные векторы и собственные значения тензора, заданного матрицей 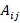 [10].
[10].
В этом примере можно сразу отметить принцип УДЕ: «совместного и одновременного изучения взаимосвязанных операций», который реализуется при решении уравнений вида:
А) 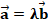 ,
, 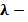 скаляр
скаляр
Б) 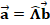 ,
, 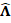 – тензор второго ранга, описываемый квадратной матрицей
– тензор второго ранга, описываемый квадратной матрицей 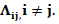
Здесь можно подчеркнуть, что в первом случае векторы 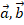 являются параллельными, а во втором – нет. Существуют направления, вдоль которых векторы остаются параллельными и в этом случае: это главные направления тензора
являются параллельными, а во втором – нет. Существуют направления, вдоль которых векторы остаются параллельными и в этом случае: это главные направления тензора 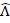 . Они играют очень важную роль и в математике и в физике. Чтобы их найти, надо перейти от случая Б) к А), то есть потребовать, чтобы все диагональные элементы матрицы
. Они играют очень важную роль и в математике и в физике. Чтобы их найти, надо перейти от случая Б) к А), то есть потребовать, чтобы все диагональные элементы матрицы 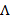 были равны:
были равны: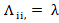 , а недиагональные равны нулю или
, а недиагональные равны нулю или 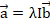 ,
, 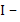 единичная матрица. Тогда получаем уравнение:
единичная матрица. Тогда получаем уравнение:
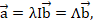
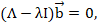
которое позволяет найти собственные значения и собственные векторы (главные направления); вдоль главных осей векторы 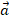 и
и 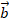 параллельны.
параллельны.
После получения искомых выражений можно привести матрицу тензора 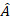 к диагональному виду в новом ортонормированном базисе. Обсуждением результатов в соответствии с технологией УДЕ решение задачи не должно заканчиваться, студентам можно предложить решить проблемы, связанные с исходной, например построить уравнение тензорной поверхности в старом и новом базисе и др.
к диагональному виду в новом ортонормированном базисе. Обсуждением результатов в соответствии с технологией УДЕ решение задачи не должно заканчиваться, студентам можно предложить решить проблемы, связанные с исходной, например построить уравнение тензорной поверхности в старом и новом базисе и др.
Результаты исследования и их обсуждение
Образовательный процесс в высшей школе отличается от школьного – больший акцент делается на самостоятельное изучение учебного материала, особое внимание уделяется практическому обучению и научно-исследовательской составляющей. В этом смысле система УДЕ может стать той методической основой, которая призвана помочь будущему выпускнику бакалавриата добиться профессионализма и личностного роста, свободно ориентироваться в меняющихся условиях.
В процессе работы со студентами факультета математики, физики и информационных технологий использовались элементы теории укрупнения дидактических единиц, как при объяснении теоретического материала, так и на практических занятиях. Для оценки качества успеваемости применялся так называемый индекс среднего балла, когда сравниваются результаты балльно-рейтинговой оценки знаний по итоговому среднему баллу в двух группах. Так, из 100 студентов первого курса примерно половина изучали рассматриваемый раздел высшей математики с привлечением элементов технологии УДЕ, во второй части традиционно вводились последовательно понятия сначала векторных, а затем тензорных величин. После подведения итогов текущего контроля (тестирования, контрольных работ) оказалось, что качество усвоения материала в контрольной группе выше примерно на 10%.
Тем не менее, ряд важных вопросов все еще остается открытым: были бы результаты другими, если бы студенты выполняли те же действия в группе, а не по отдельности; насколько повлияло каждое из действий (блочная подача лекционного материала, одновременное изучение связанных понятий, решение комплексных задач и т.д.); кроме этого, можно было бы провести ранжирование студентов группы по уровню знаний и учесть ряд других факторов.
Заключение
Одновременное изучение векторных и тензорных величин в курсе высшей математики позволяет добиться более глубокого понимания физического смысла указанных форм; свободного оперирования векторными и тензорными компонентами в выбранном ортонормированном базисе. Как показали результаты практической работы со студентами физико-математических направлений, применение системы УДЕ приводит к росту показателей по формированию нескольких компетенций, как общепрофессиональных, так и универсальных (в частности, в категории «самоорганизация и самообразование»).
Одной из целей настоящей работы было предложить способ изучения основ векторного и тензорного анализа путем введения элементов технологии УДЕ. Этот подход имеет свою учебно-методическую ценность, и для оценки результативности его применения в первом приближении было проведено сравнение результатов текущего контроля знаний по данной теме, которое показало более высокий уровень усвоения материала студентами, которые занимались в группе, где использовался метод УДЕ. Здесь особую значимость приобретает разработка кейс-зданий, которые позволяют определить качественные и количественные показатели уровня сформированности компетенций.




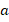
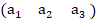 или
или 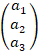
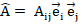
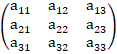
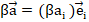
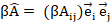
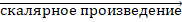
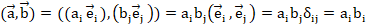
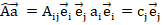
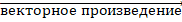
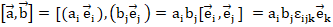
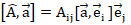
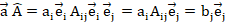
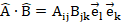
 (тензор 4-го ранга)
(тензор 4-го ранга)