Процесс обучения студентов в университетах является динамическим и требует постоянного совершенствования как из-за меняющегося уровня знаний в науке, так и из-за корректировки требований к уровню образования и к компетентности выпускников [1–3]. При этом постоянно меняются требования к содержанию образования, связанные с достижениями современной технологии, с цифровизацией технологий обучения [4–5] и пересмотром содержания образования – как в целом, так и отдельных дисциплин. Некоторые дисциплины утрачивают свою актуальность и исключаются из учебных программ, другие расширяются и укрупняются за счет включения новых разделов и объединения с ранее отдельными дисциплинами [6]. Существенное повышение эффективности изучения базовых дисциплин возможно с некоторой переориентацией учебного материала. Результат проверки остаточных знаний из раздела общих базовых у студентов оказывается близким к нулевому ввиду их оторванности от реальных задач. Большое число дисциплин рабочих программ при всей их общей целесообразности не взаимосвязаны из-за того, что они читаются разными кафедрами, и наличия многочисленных повторов материала. Это снижает интерес к обучению и приводит к большим потерям учебного времени [7]. Нет системы единого методического обеспечения, позволяющей убрать наблюдающийся многочисленный повтор материала на разных курсах, разными преподавателями. При этом наблюдается нехватка времени на изложение современного состояния вопроса. Выпускники вузов не знакомы с современными вопросами и достижениями своей специальности. Возникают проблемы с трудоустройством выпускников из-за их недостаточных знаний о современном состоянии техники. Эти проблемы известны учащимся, и это также снижает мотивацию обучения.
Цель исследования: разработка новых пакетов обучающих заданий для реализации программы непрерывности междисциплинарной подготовки по базовым дисциплинам.
Интенсивное развитие техники телекоммуникаций определяет необходимость постоянной корректировки программ подготовки специалистов с учетом требуемых компетенций. Рабочие функции специалистов систем связи довольно быстро и существенно изменяются, что определяет необходимость постоянной существенной корректировки содержания курсов или даже отказ от некоторых разделов и самих курсов, ранее считавшихся необходимыми. Переход на программы бакалавриата в технических вузах привел к прекращению подготовки инженерных кадров практически по всем (за некоторыми исключениями) специальностям. Это произошло путем поэтапного снижения учебных часов базовой подготовки и замены дисциплин базовой подготовки (или их существенным сокращением в зависимости от дисциплины в 6–10 раз) и введением и расширением дисциплин менеджмента.
Материал и методы исследования
На кафедре физики разработаны рабочие программы по основному курсу физики для всех специальностей и направлений подготовки специалистов телекоммуникации в соответствии с изменившемся числом учебных часов на подготовку. Подготовлены учебные пособия по физике для студентов, которые доступны на сайте кафедры вуза. Эти пособия включают специально разработанные индивидуальные задания для студентов, являются самодостаточными и позволяют изучать курс под руководством преподавателя самостоятельно и в дистанционном режиме. Для исследования эффективности использования этих заданий по усвоению раздела «Электромагнетизм» группа студентов вуза направления «Радиотехника» (19 человек) получила индивидуальные задания по расчету неоднородных элементов электронных схем радиотехники. Для выполнения этих заданий необходимо обобщение известных из обычных учебников курса физики результатов на случай реальных конструкций. Процесс работы над этими заданиями сопоставлялся с процессом изучения этого раздела физики в двух таких же группах аналогичной специализации (направление «Инфокоммуникационные технологии») с таким же объемом учебных часов на изучение курса физики. Подготовленные задания рассчитаны на студентов, стремящихся овладеть элементами инженерной подготовки с возможностью получения фундаментальной подготовки. Выполнение задания позволяет по индивидуальной программе углубленно осваивать разделы курса физики в процессе проведения студенческой научной работы. Предполагается, что законченная работа после ее оформления как СНИРс (в соответствии с требованиями, определяемыми издательствами) обязательно представляется на вузовских и внешних студенческих конференциях, научных форумах (кафедра на нескольких студенческих конференциях и форумах имеет свои секции). Материалы представляются к публикации в студенческих журналах и сборниках. Индивидуальные задачи, выдаваемые студентам, включают все материалы, требуемые ФГОС. Это дает возможность подготовки материалов СНИРс и перспективы продолжения более глубокого исследования по этой же или близкой теме для подготовки дипломной работы бакалавра. Ниже мы приводим примеры заданий по вопросам раздела электромагнетизма, выдаваемых студентам.
1. Метод расчета емкостей конденсаторов плоских конфигураций хорошо известен [8]. Конденсаторы являются одним из основных элементов электронных схем различного назначения. Основным параметром конденсатора является его емкость, величина которой зависит от площади пластин, расстояния между пластинами и диэлектрической проницаемости среды, заполняющей внутреннюю полость конденсатора. Расчет конденсатора с однородными параметрами и однородной средой проводится по хорошо известным соотношениям [8], и на этом по учебной программе и завершается. Вместе с тем на практике однородность структуры относительно легко обеспечить в макро- и даже микроустройствах, однако при переходе к нанодиапазону это становится проблематичным из-за особенностей технологии производства схем. Вместе с тем именно эти диапазоны являются передним краем современных технологий. Влияние неоднородностей различного типа на параметры схем представляет практический интерес. Изучение этих задач знакомит с современным состоянием технологии производства. Кроме того, неоднородность параметров в конструкции конденсатора может представлять самостоятельный интерес из-за дополнительных известных возможностей в управлении параметрами конденсатора. Предлагается рассмотреть методику расчета влияния неоднородности толщины слоя между пластинами конденсатора и неоднородности заполнения на его емкость в макроскопическом приближении для некоторых типов неоднородностей путем использования аппарата интегрирования и, как вариант, компьютерного моделирования. Показано, что для ряда конфигураций возможно аналитическое описание емкости конденсаторов с неоднородной структурой их конфигурации. Емкость конденсатора для однородных структур обычно сводится к расчету соотношения: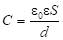
, где S – площадь перекрытия пластин конденсатора, d – расстояние между пластинами. Студенты должны уметь экстраполировать результаты, доступные школьникам, на более общие неоднородные конфигурации структур, которые встречаются на практике, должны овладеть математическим аппаратом интегрирования. Поэтому формулу расчета плоского конденсатора предлагается обобщить и взять за основу исследовательской работы. Решение этой задачи дает возможности рассчитывать параметры конденсаторов с разными типами неоднородности (среды заполнения 
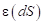, толщины 
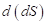, меняющихся в каждом элементе площади 
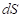). Емкость определяется путем интегрирования функции
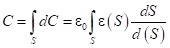, где в области малой площади 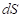конденсатор можно считать плоским.
Можно показать, что для некоторых типов неоднородностей существуют аналитические решения. Например,
1.1. При линейной функции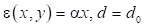
имеем:
.
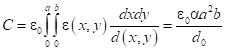1.2. При периодической форме структуры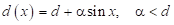
. В этом случае расчет дает значение:
.
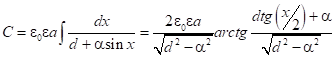С увеличением коэффициента нелинейности 0 ≤ α ≤ d (рост неоднородности при сохранении среднего расстояния между пластинами) емкость возрастает.
1.3. В клиновидной структуре, где расстояние между пластинами меняется по закону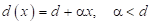 
, емкость определяется соотношением:
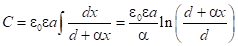
Этими примерами не ограничиваются варианты неоднородностей, для которых может быть получено аналитическое решение. Можно рассматривать различные типы функций, описывающих большое число неоднородных емкостей. Это предлагается сделать студентам в качестве самостоятельной работы уже при изучении разделов интегрирования в курсе математики. Помимо аналитических расчетов, студентам предлагается составить и проверить программу численного интегрирования своего варианта неоднородного конденсатора с сопоставлением результатов аналитического и численного расчета. Тем самым расширяется уровень познания студентов в отдельных разделах физики (в данном примере это раздел «Электричество»), математики (раздел «Интегрирование»), вычислительной техники (программирование и расчет), появляются практические навыки расчета реальных емкостей. При этом естественным путем устанавливается связь различных дисциплин и формируется непрерывность междисциплинарной подготовки. Задачи, сформулированные в курсе физики, используются далее в качестве примеров при изучении задач других дисциплин.
2. Помимо расчета неоднородных емкостей, аналогичный подход применяется для расчета сопротивлений неоднородных по форме или материалу резисторов. При передаче энергии от источника в нагрузку в макросхемах используются проводники конусообразной формы или плоские интегральные схемы в объемной или интегральной форме исполнения, сопротивление которых во многих схемах обычно из-за малого значения не учитывается. Переход к схемам микро-, а тем более нанодиапазона конструктивно потребовал использования проводников переменного сечения, концы которых имеют размер 10-3– 10-6 м. Поэтому анализ методов оптимального подключения от проводников обычных размеров к схемам микро- и нанодиапазонов представляет актуальную задачу. Сопротивление резисторов и проводников цилиндрической формы, заполненных однородным материалом с постоянным по всей длине проводника сечением, рассчитывается по формуле [8]: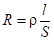 
, где ρ – удельное сопротивление проводника (зависит от материала), S – площадь поперечного сечения проводника, l – длина проводника. Для описания зависимости сопротивления неоднородного проводника переменного сечения необходимо использовать более общее выражение:
,
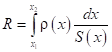где x1 и x2 – начало и конец проводника с переменной шириной сечения.
Для токопроводящего полоска толщиной δ из однородного металла, ширина которого зависит от координаты x и описывается функцией y(x), сопротивление определяется в виде:
.
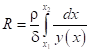Последнее соотношение позволяет рассчитать сопротивление для проводников самых разных форм. Для большого числа конфигураций можно получить аналитические выражения для расчета сопротивления или воспользоваться численными методами. Рассмотрим простейшие конфигурации, для которых можно получить аналитическое решение.
2.1. Конусовидная зависимость ширины полоска, описываемая функцией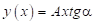 
, дает соотношение для расчета сопротивления проводника в виде:
.
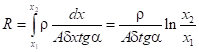Из формулы следует, что сопротивление конусообразного проводника уменьшается при увеличении угла у вершины конуса α. Использование клиновидной структуры снижает степень роста сопротивления проводника с увеличением его длины.
2.2. Проводник в виде полоска с экспоненциальной зависимостью ширины полоска, описываемой функцией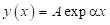 
, характеризуется сопротивлением:
.
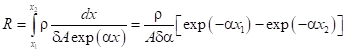2.3. Проводник с поперечным размером, описываемым функцией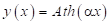
, характеризуется сопротивлением, определяемым соотношением:
.
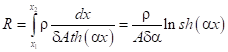Полученные результаты показывают зависимость сопротивления проводников от формы, проявляющуюся наиболее существенно в области малых сечений. Таким образом, при малых размерах поперечного сечения необходимо учитывать форму проводника. Аналогично можно рассмотреть катушки индуктивности с неоднородными элементами. В учебных и в научных задачах можно предложить большое число неоднородных структур, расчет которых требует привлечения аппарата интегрирования (аналитического или численного).
Результаты исследования и их обсуждение
Проводилось сравнение результатов освоения учебного материала по одинаковой теме в группе с индивидуальными заданиями и в аналогичных параллельных группах, изучающих курс физики по традиционной программе, с одинаковым числом студентов, по нескольким показателям. При тестировании по обычным тестам раздела «Электромагнетизм» студенты контрольных групп, изучающие курс физики по традиционной программе, показали удовлетворительное усвоение материала в пределах от 40% до 60% и не проявили интереса к изучавшейся теме. Студенты, выполняющие индивидуальные работы, с теми же тестами, которые выдавались для контрольных групп, справились на 100% и оценили их как простые. При этом они выразили желание выполнять более сложные и интересные задания, чтобы иметь возможность повысить свою самооценку. Другим результатом исследования явилось то, что у студентов, выполнивших индивидуальные комплексные задания, на руках оказывались готовые научно-исследовательские работы. Эти работы они представляли на студенческие научные конференции разного уровня, а наиболее интересные работы после оформления публиковались в студенческих научных журналах. В аналогичных группах с традиционной методикой обучения такая возможность отсутствует. В этих группах студенческая научная работа проводится только наиболее успевающими студентами не из-за личного желания, а часто за счет некоторого давления со стороны преподавателей. У студентов экспериментальной группы резко выросли мотивация обучения и желание проведения новых исследований, которые можно было бы представлять на студенческие конкурсы разного уровня. Минусом полученных результатов является сложность работы по индивидуальным заданиям с большим числом учащихся из-за недостатка времени у преподавателей на работу с каждым студентом. Для высокой эффективности работы по предлагаемой методике необходима индивидуальная работа с каждым студентом, время на которую не предусматривается учебными планами.
Заключение
Реализация программы непрерывности междисциплинарной подготовки и повышения ее эффективности возможна только при разработке специальной рабочей программы, где изучение отдельных тем будет увязано с вопросами, входящими в предмет изучения другой дисциплины. Наибольший эффект достигается в том случае, когда ставится и решается комплексная задача, в которой используются знания разных дисциплин, которые не разделены искусственно, а используются совместно. Разработаны задачи расчета неоднородных элементов электрических схем, требующие изучения и применения разделов физики, интегрирования и программирования. Показана возможность получения аналитических решений для большого числа новых конфигураций, ранее не рассматривавшихся в литературе, на основе которых возможно создание планарных элементов микро- и наноразмеров для различных диапазонов частот. Решение этих задач позволяет естественным путем освоить темы, относящиеся в настоящее время к разным учебным дисциплинам.