Технологический прогресс, возникновение и развитие сети Internet привели к глобальным изменениям во всех сферах человеческой жизни, в том числе и в образовании. Актуальным направлением развития системы высшего образования является подготовка кадров, способных эффективно решать профессиональные задачи в условиях постоянных, непредсказуемых и быстрых изменений. Для описания новой реальности уже привычно используется термин VUCA-мир – мир, характеризующийся нестабильностью (volatility), неопределенностью (uncertainty), сложностью (complexity) и неоднозначностью (ambiguity). Пандемия вируса COVID-19 является примером вызова VUCA-мира, затронувшим все сферы человеческой деятельности и обострившим проблему соответствия модели выпускника высшей школы требованиям общества. Важными составляющими компонентами компетентностной модели современного специалиста являются метапредметные (способность учиться самостоятельно, работать с информацией, адаптироваться к новым условиям профессиональной деятельности), предметные (применять предметные знания и цифровые инструменты для решения профессиональных задач) и личностные (способность эффективно взаимодействовать в команде и нестандартно мыслить при решении профессиональных задач) компетенции.
Трансформация целей обучения в высшей школе определила развитие новых образовательных технологий. В «Стратегии развития информационного общества в Российской Федерации на 2017-2030 годы» отмечена необходимость использования различных образовательных технологий, в том числе дистанционных, при реализации образовательных программ [1].
Понятие «дистанционные образовательные технологии» определено в Федеральном законе «Об образовании в Российской Федерации» (№ 273-ФЗ от 29.12.12 г. с изменениями 2020г.) как «образовательные технологии, реализуемые в основном с применением информационно-телекоммуникационных сетей при опосредованном (на расстоянии) взаимодействии обучающихся и педагогических работников». Федеральные государственные образовательные стандарты высшего образования допускают использование вузами дистанционных образовательных технологий при реализации образовательных программ бакалавриата и магистратуры.
Принимая во внимание сложную эпидемиологическую обстановку в мире, трудно сегодня представить вуз, не использующий в той или иной мере дистанционные образовательные технологии. Распространенным инструментом внедрения дистанционных образовательных технологий являются электронные системы управления обучением. Одной из самых популярных систем управления обучением в российских и зарубежных университетах является LMS Moodle (модульная объектно-ориентированная динамическая учебная среда), получившая широкое распространение благодаря понятному интерфейсу, функциональным возможностям и бесплатному распространению [2].
Однако эффективность применения дистанционного обучения зависит не только от используемых информационных технологий, но и от методических подходов к обучению [3-5]. В связи с этим рассматривается проблема разработки теоретических и методических основ дистанционного обучения студентов математическим дисциплинам на базе LMS Moodle. Решить данную проблему можно на основе профессионально-деятельностного подхода к обучению [6], объединяющего положения системно-деятельностного и профессионально направленного подходов.
Целью предпринятого исследования является разработка с позиций профессионально-деятельностного подхода электронного учебного курса (ЭУК) по математическому анализу для студентов экономических направлений подготовки с помощью электронно-образовательной системы LMS Moodle.
Материал и методы исследования. Результатом математической подготовки в вузе является математическая компетентность специалиста, которая большинством исследователей (Т.Л.Анисова, Н.А.Бурмистрова, Л.Н.Журбенко, Л.К.Илященко, Л.Д.Кудрявцев, В.А.Шершнева, Л.В.Шкерина, С.А.Шунайлова и др.) рассматривается как составляющая его профессиональной компетентности, её проекция на предметную область математики.
Ведущая идея профессионально-деятельностного подхода к обучению заключается в следующем: при разработке целей обучения предмету необходимо, прежде всего, выделить систему типовых профессиональных задач будущего специалиста, для решения которых требуются предметные знания. Поэтому под математической компетентностью специалиста мы понимаем его способность и готовность решать типовые профессиональные задачи (ТПЗ), требующие применения математических знаний [6]. Такой подход позволил обосновать и произвести отбор содержания математической подготовки специалиста в вузе как совокупности математических знаний, необходимых для выполнения всех действий методов решения задач будущей профессиональной деятельности.
Выделенное описанным выше способом содержание дисциплины «Математический анализ» было структурировано в учебные модули, целью которых является обучение отдельным действиям обобщенных методов решения ТПЗ или обобщенному методу в целом. Модульная структура учебного курса позволила систематизировать его содержание по типам решаемых задач, дала возможность получения регулярной «обратной связи» от студентов, позволила выстроить индивидуальную образовательную траекторию студентов в зависимости от профиля и формы подготовки.
Изучение всех учебных модулей проводится в два этапа: дисциплинарный и междисциплинарный. Дидактическим средством реализации дисциплинарного этапа являются системы математических задач установленных типов, а междисциплинарного этапа – псевдопрофессиональные задачи (математические задачи с профессиональным контекстом). Все учебные модули в ЭУК имеют одинаковую структуру, что позволяет студентам легко ориентироваться в учебном материале.
Разработка электронного учебного курса «Математический анализ» включала следующие этапы:
· определение в качестве цели ЭУК обучение методам решения типовых задач математического анализа как систему опорных знаний, необходимых для будущей профессиональной деятельности;
· отбор содержания ЭУК (опорных знаний по математическому анализу) по авторской методике [7];
· определение структуры ЭУК как совокупности учебных модулей (разделов, тем) математического анализа, в рамках которых формируются опорные знания;
· выделение для каждого учебного модуля системы типовых математических задач и методов их решения;
· разработка дидактических средств обучения методам решения типовых математических задач и контроля знаний;
· разработка псевдопрофессиональных задач для каждого учебного модуля;
· размещение разработанных дидактических материалов в LMS Moodle;
· внедрение ЭУК в учебный процесс.
В статье приведены результаты разработки ЭУК по математическому анализу для студентов экономических направлений подготовки на основе профессионально-деятельностного подхода, внедрение которого позволило повысить итоговый показатель успеваемости студентов по данной дисциплине.
Результаты исследования и их обсуждение. Организация дистанционного обучения в Астраханском государственном университете осуществляется на базе LMS Moodle, что потребовало предварительного обучения профессорско-преподавательского состава. В настоящее время разработаны ЭУК практически по всем дисциплинам, которые используются для организации дистанционного и смешанного обучения студентов очной, очно-заочной и заочной форм обучения по всем направлениям и уровням подготовки.
Рассмотрим особенности разработки ЭУК по математическому анализу для бакалавров экономических направлений подготовки. Структура курса состоит из метаданных и учебных модулей (рис. 1).
Метаданные курса включают название курса, информацию об авторе и направлении подготовки обучающихся студентов, рабочую программу дисциплины (аннотация, количество часов, формируемые компетенции студентов, тематический план, содержание, примеры контрольных заданий, вопросы к экзамену, список рекомендуемой литературы), словарь терминов, файлы с учебно-методической литературой и объявления преподавателя.
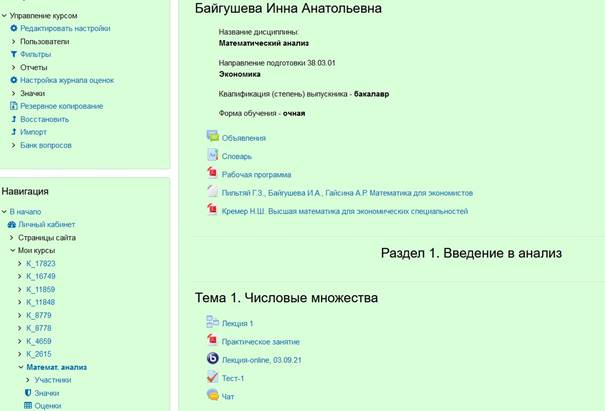
Рис. 1. Структура курса
Содержание курса математического анализа представлено 15 учебными модулями (темами), объединенными в 4 раздела: «Введение в анализ» (4 модуля), «Дифференциальное исчисление функций одной переменной» (3 модуля), «Интегральное исчисление функций одной переменной» (3 модуля), «Дифференциальное исчисление функций нескольких переменных» (3 модуля), «Ряды» (2 модуля).
Структура учебных модулей включает следующие компоненты: краткий теоретический материал, подробный разбор методов решений типовых задач, примеры решения псевдопрофессиональных задач, задачи для самостоятельного решения, тесты для самоконтроля, площадка для интерактивного взаимодействия преподавателя и студентов. Отдельные учебные модули могут содержать дополнительно: видеоматериалы, онлайн-лекции, развернутые задания. Например, модуль «Числовые множества» (рис. 1) включает ещё информацию об онлайн-лекции. Между модулями в соответствии с рабочей программой дисциплины содержатся контрольные задания. Правильно структурированные материалы облегчают их размещение [8], а также работу студентов и преподавателя.
В каждом учебном модуле необходимо выделить ориентировочную основу учебной деятельности – математические знания данного модуля, основные типы математических задач, при решении которых применяются знания модуля и обобщенные методы их решения. Например, ориентировочную основу модуля «Дифференциальное исчисление функций одной переменной» дисциплины «Математический анализ» составляют математические понятия «производная», «дифференциал», «дифференцируемая функция», «экстремумы функции», «формула Тейлора», а также утверждения (теоремы) по установлению свойств, взаимосвязи и применению данных понятий.
Для изложения материала в системе LMS Moodle используется элемент «Лекция», который может содержать гиперссылки на необходимые источники информации (учебники, учебно-методические пособия, видеоматериалы). В содержание лекции необходимо включать задания на проверку понимания сути изучаемых понятий и вопросы для самопроверки, не позволяющие изучать новый материал, пока не получены верные ответы.
Рассматриваемый модуль содержит семь основных типов задач: «Нахождение производных и дифференциалов функций», «Нахождение касательной и нормали к графику функции», «Нахождение локальных экстремумов функций», «Нахождение глобальных экстремумов функций», «Исследование свойств и построение графика функции», «Нахождение пределов функции по правилу Лопиталя», «Приближенное вычисление значений функции». Каждой задаче соответствует обобщенный метод решения, позволяющий решить любую задачу данного типа.
Например, обобщенный метод решения задачи «Нахождение локальных экстремумов функций» состоит из следующих действий [9]:
1. Найти область определения функции 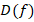 .
.
2. Найти производную функции.
3. Найти стационарные и критические точки, опираясь на необходимое условие существования экстремума.
4. Разбить 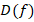 на интервалы стационарными и критическими точками.
на интервалы стационарными и критическими точками.
5. Определить знак производной в каждом интервале.
6. Определить точки экстремума функции, опираясь на достаточное условие существования экстремума.
7. Вычислить экстремумы функции.
Для представления методических материалов, в которых рассмотрены обобщенные методы решения типовых математических задач по математическому анализу, примеры их реализации и задачи для самостоятельной работы, в учебном модуле используется элемент «Практическое занятие». Для освоения метода студенты должны многократно применить его для решения задач соответствующего типа.
Элемент учебного модуля «Тест» предназначен для оценки освоения студентами учебного материала. В LMS Moodle тест создается на основе банка вопросов, куда можно включать вопросы разных типов по категориям, соответствующим учебным модулям дисциплины. При создании Банка вопросов по дисциплине «Математический анализ» нами использовались вопросы таких типов, как «Числовой ответ», «Множественный выбор», «На соответствие», «Эссе». В настройках теста можно устанавливать ограничение по времени, количество попыток для студента, метод оценивания, порядок и свойства вопросов в тесте, доступную студентам информацию [10].
Преподаватель при оценке уровня сформированности метода должен иметь возможность проверить не только результат решения, но и соблюдение последовательности выполнения всех действий метода. Для этого удобно использовать вопрос типа «эссе», для ответа на который студенты могут прикрепить файл с решением. Такой тип вопроса преподаватель оценивает «вручную», остальные типы вопросов можно оценивать автоматически. Рассмотрим решение задачи «Нахождение локальных экстремумов функций», выполненное студентом в соответствии с алгоритмом обобщенного метода решения в качестве ответа на вопрос «Эссе».
Задача. Найти экстремумы функции 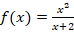 [7].
[7].
Решение. 1. Данная функция определена для всех действительных чисел, кроме 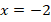 . Следовательно,
. Следовательно, 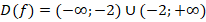 .
.
2. Дифференцируя частное, получим 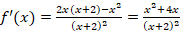 .
.
3. Очевидно, что производная также определена при всех x, кроме 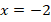 , значит критических точек нет. Из уравнения
, значит критических точек нет. Из уравнения 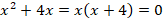 находим стационарные точки
находим стационарные точки 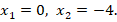
4. Разобьем область определения функции 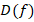 стационарными точками на интервалы
стационарными точками на интервалы 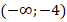 ,
, 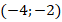 ,
, 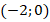 ,
, 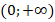 , в каждом из которых производная сохраняет знак.
, в каждом из которых производная сохраняет знак.
5. Найдем знаки производной в этих интервалах (рис. 2).
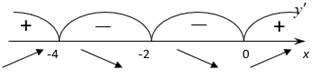
Рис. 2. Определение знака производной функции в области её определения
6. В окрестностях стационарных точек 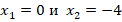 производная меняет знак, значит, они являются точками экстремума:
производная меняет знак, значит, они являются точками экстремума: 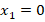 – точка минимума,
– точка минимума, 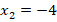 – точка максимума.
– точка максимума.
7. Вычислим экстремумы функции: 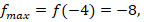
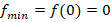 .
.
В тесты включены псевдопрофессиональные задачи разных типов, для решения которых требуются математические знания изученного учебного модуля. Пример такой задачи из теста учебного модуля «Дифференциальное исчисление функций одной переменной», оформленной в виде вопроса «Числовой ответ», представлен на рисунке 3.
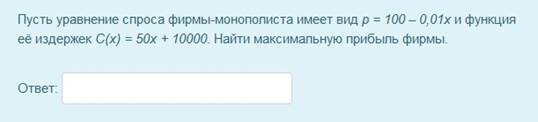
Рис. 3. Пример вопроса «Числовой ответ» с псевдопрофессиональной задачей
Для решения представленной выше задачи (рис. 3) используется сформированный при изучении данного учебного модуля обобщенный метод решения задачи «Нахождение локальных экстремумов функций». Действительно, сначала следует составить функцию общего дохода фирмы 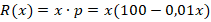 , тогда функция прибыли будет иметь вид
, тогда функция прибыли будет иметь вид 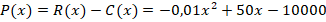 . Затем, выполняя действия 1-7 обобщенного метода, студенты находят максимальное значение прибыли 52500 усл. ед.
. Затем, выполняя действия 1-7 обобщенного метода, студенты находят максимальное значение прибыли 52500 усл. ед.
Для выставления итоговой оценки по дисциплине «Математический анализ» был создан тест, составленный случайным образом из вопросов разных категорий банка вопросов.
Для обмена сообщениями между студентами и преподавателем при дистанционном режиме обучения в LMS Moodle предусмотрены элементы «Чат» и «Форум».
Заключение. Как показала практика, внедрение в учебный процесс ЭУК «Математический анализ» для экономических направлений подготовки бакалавров, разработанного на платформе LMS Moodle, позволяет студентам в дистанционном режиме освоить обобщенные методы решения типовых математических задач, научиться использовать эти методы для решения задач будущей профессиональной деятельности. Кроме предметных результатов обучения, у студентов формируются такие ключевые компетенции, как умение грамотно использовать цифровые технологии, навык самоорганизации познавательной деятельности. Разработанный ЭУК можно использовать и при смешанном режиме обучения для организации самостоятельной учебной работы студентов и оценки результатов обучения.



