Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В России ежегодно миллионы школьников принимают участие в предметных олимпиадах, направленных выявление и поддержку одаренной молодежи.  В статье Е.А. Кротовой и О.М. Филатовой, посвященной олимпиадному движению школьников, отмечается, что участие в предметных олимпиадах «способствует развитию творческой активности и становлению профессионального самоопределения будущего выпускника» [1].

Министерство науки и высшего образования и Министерство просвещения Российской Федерации являются соорганизаторами олимпиад школьников по иностранным языкам (см. [2, 3]), интерес к которым традиционно высок. Так, согласно перечню [2], в 2020/2021 учебном году количество таких олимпиад  составило 19.

Значительная часть научных работ, посвященных исследованию олимпиад по иностранным языкам, нацелена на проведение теоретического анализа выполнения конкурсных олимпиадных заданий и формулирование методических рекомендаций педагогам [4, 5]. Так, в работе Н.А. Бесядовской и Н.И. Трубицыной [6] предлагается методика проведения анализа олимпиадных тестовых заданий с применением инструментов математической статистики. Такой подход позволяет авторам, в частности, выявлять типичные ошибки школьников при выполнении олимпиадных заданий и конкурсов, возможные причины их появления и формулировать на основе проведенного анализа рекомендации по их устранению.

Олимпиадные задания по иностранному языку носят интегрированный характер, сочетая разные формы и объекты контроля. Например, заключительный этап анализируемой олимпиады по французскому языку включает 5 конкурсов, соответствующих уровню сложности В2+ по европейской шкале, из которых четыре проводятся в письменной форме [7].

Цель настоящего исследования – на основе статистических методов исследования показать соответствие методическому принципу системности комплекта олимпиадных заданий Всероссийской олимпиады школьников (ВсОШ) по иностранному языку (на примере заключительного этапа по французскому языку).

Материал и методы исследования

Всероссийская олимпиада школьников по французскому языку проводится с 2002 г. В таблице 1 приведены результаты заключительного этапа данной олимпиады за последние 5 лет (в 2020 г. заключительный этап не проводился в связи с эпидемией COVID-19).

Таблица 1

Результаты участников заключительного этапа ВсОШ по французскому языку 2017–2021 гг.

Как видно, итоговые результаты в динамике по годам являются достаточно однородными, что обеспечивается утвержденным Порядком проведения Всероссийской олимпиады школьников в части норм определения победителей и призеров [8], а также единым подходом к разработке олимпиадных заданий, соответствующих уровню сложности В2+ по европейской шкале. Таким образом, не ограничивая общности, для достижения поставленной исследовательской цели можно выбрать произвольный год проведения олимпиады. 

В соответствии с утвержденным порядком проведения ВсОШ на официальном сайте олимпиады в сети Интернет в обязательном порядке размещаются итоговые результаты и олимпиадные работы только победителей и призеров. Однако для достижения исследовательской цели необходимо не только провести анализ итоговых результатов участников, но и детально проанализировать баллы по всем конкурсным заданиям. Исследовав опубликованные на официальных сайтах ВсОШ по французскому языку данные за последние пять лет, мы выбрали для анализа заключительный этап 2018 г. как последний, по которому доступны результаты всех участников олимпиады (включая и школьников, не ставших призерами) по всем конкурсным заданиям. Таким образом, были проанализированы результаты всех 196 участников [9].

В состав исходных показателей исследования вошли результаты участников по пяти конкурсам и итоговый балл:

1-й конкурс (ЛГТ) – лексико-грамматический тест (максимально возможное количество баллов – 40) с оцениванием по ключу;

2-й конкурс (ТПУТ) – тест на понимание устного текста (максимально возможное количество баллов – 30) с оцениванием по ключу;

3-й конкурс (ТППТ) – тест на понимание письменных текстов (максимально возможное количество баллов – 30) с оцениванием по ключу;

4-й конкурс (КПР) – конкурс письменной речи (максимальное количество баллов – 20) с оцениванием по критериям;

5-й конкурс (КУР) – конкурс устной речи (максимальное количество баллов – 20) с оцениванием по критериям;

итоговый балл (ИБ) – сумма баллов участника олимпиады за выполнение всех олимпиадных заданий.

Для анализа результатов применялись статистические методы: процедуры описательной статистики и корреляционный анализ.

Результаты исследования и их обсуждение

Участниками заключительного этапа Всероссийской олимпиады по французскому языку становятся обучающиеся, достижения которых соответствуют критериям отбора, установленным Минобрнауки России. В частности, это участники регионального этапа олимпиады, набравшие необходимое для участия в заключительном этапе олимпиады количество баллов.

Порядок определения победителей и призеров заключительного этапа олимпиады устанавливается квотой Минобрнауки России: число победителей и участников «составляет не более 45% от общего числа участников заключительного этапа олимпиады предыдущего года; они должны иметь не менее 50% от максимально возможного количества итоговых баллов, при этом число победителей не должно превышать 8% от общего числа участников заключительного этапа» [10].

В 2018 г. из 196 школьников, принявших участие в олимпиаде по французскому языку, чьи результаты вошли в итоговый протокол, 13 стали победителями с результатом 119–127 баллов и 76 – призерами (106–118 баллов). В таблице 2 приводятся рассчитанные показатели описательных статистик результатов по всем конкурсам и итоговым баллам, среди который есть, в частности, мода (значение в множестве данных, которое встречается наиболее часто) и медиана (значение, которое делит упорядоченное множество точно пополам).

Следует отметить, что для итогового балла мода, равная 106, совпала с нижней границей баллов у призеров, а значение медианы 104 ниже значения моды, что может косвенно свидетельствовать о том, что установленный порядок определения победителей и призеров представляет собой достаточно точный «измерительный прибор»: все победители и призеры входят в «половину» участников с высокими баллами.

Таблица 2

Описательные статистики результатов

Размах, дисперсия и стандартное отклонение являются мерами изменчивости. Например, значения дисперсии и стандартного отклонения характеризуют разброс значений баллов вокруг среднего значения. Если дисперсия близка к нулю, то это означает, что школьники одинаково ровно выполняют их, а значит, конкурсные задания плохо дифференцируют испытуемых по уровням владения иностранным языком и не могут адекватно ранжировать участников олимпиады. Большие значения дисперсии могут вызываться различными факторами, такими как:

- неоднородность группы участников олимпиады (согласно положению [10], от некоторых регионов в качестве финалистов направляется один школьник, который на региональном этапе набрал наибольшее количество баллов, но не являющееся необходимым для участия в заключительном этапе);

- незнакомые для части аудитории конкурсные задания или недостаточно ясные формулировки и т.п.

Анализируя показатели дисперсии и стандартного отклонения, представленные в таблице 2, можно сделать вывод, что конкурсные олимпиадные задания позволяют достаточно хорошо дифференцировать участников по уровням.

Обязательным требованием многих статистических методов является то, что анализируемые данные распределены нормально. Результаты тестирований при больших выборках обычно имеют распределение, близкое к нормальному. Такое распределение имеет колоколообразную форму, значения его моды, медианы и среднего арифметического равны. Анализ показателей моды, медианы и среднего арифметического таблицы 2 и графиков результатов олимпиадных конкурсов (рис. 1–5) позволяет предполагать, что результаты имеют распределения, близкие к нормальному.

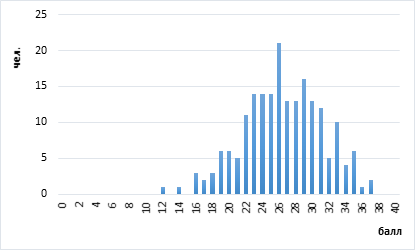
Рис. 1. График результатов лексико-грамматического теста

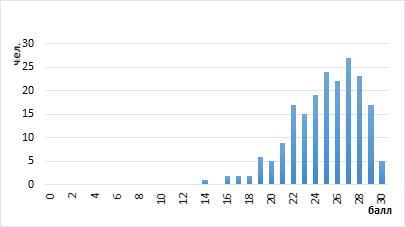
Рис. 2. График результатов понимания устного текста

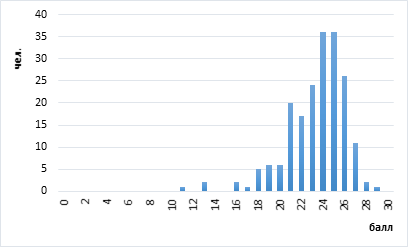
Рис. 3. График результатов понимания письменных текстов

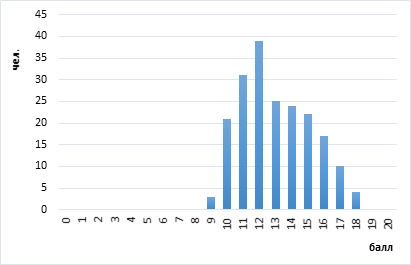
Рис. 4. График результатов конкурса письменной речи

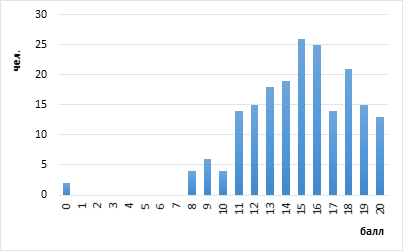
Рис. 5. График результатов конкурса устной речи

Для точного установления факта нормальности распределений применим критерии асимметрии и эксцесса. Сравнивая выборочные показатели асимметрии A и эксцесса E (табл. 2) с критическими значениями 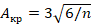 ,  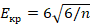, где n = 196, можем утверждать, что результаты лексико-грамматического теста и конкурса письменной речи соответствуют нормальному закону, распределения прочих результатов отличаются от нормального. В связи с этим фактом для исследования взаимосвязи результатов олимпиадных конкурсов будет применяться метод ранговой корреляции.

Корреляционный анализ выступает в качестве одного из инструментов проверки валидности отдельных заданий. При разработке конкурсных этапов и заданий нужно стремиться к тому, чтобы корреляция результатов была достаточно высокой. Однако коэффициент корреляции между отдельными конкурсами не должен быть очень близким к 1, поскольку это может означать, что задания начинают дублировать друг друга: одно из них фактически является лишним.

В таблице 3 приведены рассчитанные значения коэффициентов ранговой корреляции Спирмена.

Таблица 3

Корреляционная матрица

Таким образом, корреляционный анализ демонстрирует наличие тесной связи между всеми конкурсами заключительного этапа Олимпиады и итоговым результатом: все коэффициенты ранговой корреляции Спирмена значимы на уровне 0,01. При этом следует отметить, что для конкурсов показателей корреляции, близких по модулю к 1, нет, что свидетельствует о том, что данные олимпиадные задания не находятся в «слишком тесной связи», подменяя друг друга. В то же время следует отметить, что итоговый балл находится в очень тесной связи с каждым отдельным олимпиадным конкурсом.

Заключение

Проведенный статистический анализ результатов школьников заключительного этапа Всероссийской олимпиады по французскому языку, включающий 5 конкурсов, соответствующих уровню сложности В2+ по европейской шкале, показал соответствие комплекта олимпиадных заданий методическому принципу системности. Олимпиадные задания носят интегрированный характер, сочетая разные формы и объекты контроля; позволяют достаточно хорошо дифференцировать участников по уровням. Корреляционный анализ подтверждает тот факт, что олимпиадные конкурсы по иностранным языкам не дублируют друг друга, а образуют целостную систему.