Траекторию включения дисциплин математического содержания и вектор интеграции профессиональных дисциплин с областями математического знания, математическими методами и информационными технологиями в разрабатываемых профессиональными образовательными организациями образовательных программах во многом обусловила Концепция развития математического образования в Российской Федерации [1], в которой, кроме обоснования важности математики для «создания инновационной экономики, реализации долгосрочных целей и задач социально-экономического развития Российской Федерации», перечислены также основные проблемы развития математического образования:
– проблемы мотивационного характера (связанные с недооцененностью математического знания, с упущением важности изучения математических дисциплин в профессиональном становлении личности и будущего специалиста – выпускника образовательных программ высшего образования любых направлений подготовки/специальностей, с отсутствием механизмов повышения мотивации и инструментария стимулирования обучающихся, активно использующих математические методы в своей учебно-образовательной и научно-исследовательской деятельности, и т.д.);
– проблемы содержательного характера (связанные с устареваемостью наполнения и несоответствием содержания рабочих программ математических курсов реальным требованиям современного научно-технического прогресса, запросам работодателей и (или) профессиональных сообществ, с отсутствием реальной интеграции математического знания в содержание профилирующих профессиональных дисциплин и т.д.);
– кадровые проблемы (связанные с нехваткой профессиональных квалифицированных кадров – специалистов высокого класса, способных не только обучить студентов в профессиональном плане, но и сформировать у них жизненные интересы, в том числе путем развития организационно-методических навыков).
Основные позиции и положения Концепции развития математического образования трансформировались в том числе и в требования ФГОС ВО в форме соответствующих компетенций. Если в учебно-методическом обеспечении основной профессиональной образовательной программы высшего образования (далее – ОПОП ВО) по направлению подготовки 06.03.01 Биология [2] в соответствии со ФГОС ВО (так называемом стандартом 3+) к дисциплине «Математика и математические методы в биологии» привязаны общепрофессиональные и профессиональные компетенции (такие как ОПК-1, ПК-1 и ПК-8), то в актуализированном ФГОС ВО (так называемом стандарте 3++) [3] перечень компетенций, которые могут быть сформированы в том числе при помощи математических дисциплин, несколько увеличился, и в основном это компетенции «общего» плана – универсальные и общепрофессиональные. Здесь прослеживаются позиция государства и видение академического сообщества в части важности освоения элементов математического знания при обучении по всем направлениям подготовки/специальностям профессионального образования независимо от профиля осваиваемой образовательной программы.
Эффект от изучения математических курсов при обучении по непрофильным образовательным программам, а также влияние математической подготовки обучающихся на их общую профессиональную подготовку рассматривали и многие научные исследователи. Методическую составляющую повышения качества профессиональной математической подготовки выпускников профильных образовательных программ посредством профессионально ориентированного обучения рассматривали А.Г. Мордкович [4], И.И. Баврин [5], В.А. Гусев [6] и др. Ими была заложена основа для изучения влияния математических дисциплин на профессиональную подготовку обучающихся уже по непрофильным направлениям подготовки/специальностям в различных областях знания:
– особенности построения содержания математически курсов и вопросы профессиональной направленности обучения математике студентов горных факультетов вузов как средство формирования их математической компетентности рассматривала М.С. Аммосова [7];
– методику формирования творческой самостоятельности студентов технических вузов в обучении математике с использованием системы «Mathematica» систематизировала Ф.А. Ихсанова [8];
– контекстный подход к формированию прогностической компетенции при обучении высшей математике студентов естественно-научного направления смоделировала О.М. Растопчина [9];
– методической системе мониторинга качества профессиональной математической подготовки студентов вуза посвящено диссертационное исследование Т.А. Табишева [10];
– методику реализации профессиональной направленности обучения математике студентов экологических направлений подготовки обосновала С.И. Торопова [11].
Следует отметить, что в каждом из указанных исследований приведены некоторая модель построения оценочного блока образовательной деятельности и описание изучения процесса формирования определенных знаний, умений и навыков обучающихся в пределах конкретной учебной дисциплины. Однако данные исследования не затрагивают вопрос влияния изучения математических дисциплин на формирование организационно-методических навыков и методику выделения факторов повышения успеваемости и качества профессиональной математической подготовки обучающихся по непрофильным образовательным программам, что обусловливает актуальность настоящего исследования. Предложенная в статье модель формирования организационно-методических навыков устанавливает межпредметный характер повышения успеваемости и качества подготовки обучающихся, чем выгодно отличается от аналогичных систем и моделей.
Цель исследования
Важной составной частью организации и осуществления образовательной деятельности в любой ОО ВО является создание условий для более успешного усвоения студентами изучаемых дисциплин в течение всего процесса обучения, на каждом его этапе. Для достижения лучших показателей по успеваемости студентов, в частности по непрофилирующим дисциплинам, необходимо решить целый ряд задач, а именно:
1) выявить причины, мешающие студентам учиться адекватно своим способностям;
2) выработать механизмы, устраняющие или уменьшающие негативные влияния этих причин;
3) создать условия для формирования у студентов организационно-методических навыков.
На самом деле факторов, оказывающих влияние на успеваемость обучающихся, достаточно много. Это могут быть социальные причины – неблагополучная семья, низкий материальный уровень, средства массовой информации и т.д.; физиологические особенности – заболевания, питание, гендерные аспекты и т.д.; психологические аспекты – индивидуальные личностные характеристики обучающегося, мотивация, интересы и т.д.
Условно причины, которые не позволяют студентам учиться адекватно своим способностям, можно разделить на группы – объективные и субъективные.
К объективным причинам, следуя результатам исследований И.И. Мамаева и В.П. Шибаева [12], с позиции обучающихся необходимо отнести низкое качество подготовки студентов к учебным занятиям.
К субъективным причинам, мешающим студентам учиться, прежде всего, можно отнести неумение планировать свой труд во время самостоятельной работы, нежелание своевременно восстанавливать конспекты пропущенных занятий, постоянный перенос и оттягивание выполнения и защиты заданий, лабораторных и различных работ. На лекциях многие студенты остаются пассивными слушателями, не утруждая себя пониманием материала. Они автоматически перерисовывают с доски (слайда), что-то записывают по принципу «потом разберусь», а это «потом» наступает нередко лишь во время сессии, когда уже нет времени ни разобраться, ни понять. В результате студент попадает в категорию «задолжников».
Нередко выявляются также и такие факторы, как педагогическое влияние – мы не учим студентов, но требуем от них знать и уметь; мы не учим студентов писать конспект лекций, конспектировать материалы к практическим занятиям, пользоваться библиотечными ресурсами и так далее, считая, что студенты все это знают и умеют. Огромное значение в обучении студентов дисциплинам «непрофильного» уклона, в том числе математических курсов, играет кадровый состав – научно-педагогические работники, которые реализуют данные дисциплины. Их владение словом, содержанием своего курса, способность заинтересовать обучающихся и мотивировать их к дальнейшему успешному освоению своего курса в большинстве случаев играют первостепенную роль в повышении успеваемости студентов.
Перечисленные факторы и ряд других причин приводят к тому, что перед сессией начинается «штурмовщина», которая не способствует усвоению учебного материала, а лишь вызывает у студентов ажиотаж, нервозность, депрессию, вследствие чего они физически не успевают отчитаться по всем учебным дисциплинам семестра и получают академические задолженности, в том числе и по математическим курсам.
Материал и методы исследования
Для уменьшения влияния этих негативных причин нами была разработана модель организации учебных занятий, сущность которой заключается в следующем.
На одном из первых практических занятий преподаватель излагает студентам причины, которые не позволяют им учиться адекватно своим способностям, и предлагает в каждой группе избрать ответственного по дисциплине студента (далее – ОДС). Студенты группы открытым голосованием избирают такого человека по изучаемой дисциплине. В его обязанности входит:
§ обеспечивать в течение семестра своевременное выполнение студентами группы всех установленных заданий и их защиту (представление, презентацию);
§ добиваться своевременного восстановления конспекта лекции студентами, пропустившими учебные занятия;
§ информировать студентов группы, пропустивших учебные занятия (учебное занятие), об имеющихся заданиях и (или) указаниях преподавателя;
§ организовывать коллективное решение отдельных задач, совместное рассмотрение наиболее сложных вопросов, проблемных кейсов и ситуационных задач;
§ обеспечивать подготовку студентов группы ко всем видам учебных занятий, текущим, рубежным и промежуточным аттестациям;
§ информировать преподавателя о персональной готовности группы к занятиям;
§ согласовывать с преподавателем время проведения дополнительных консультаций при возникновении трудностей в усвоении учебного материала и выполнении самостоятельных заданий [13].
Рабочим документом для ОДС является «Карта динамики успеваемости студентов группы» (далее – карта), фрагмент которой представлен в таблице. В первом столбце указывается номер студента по журналу, во втором – фамилии и инициалы. Против каждой фамилии студента по горизонтали расположены квадраты, число которых совпадает с числом занятий по данной дисциплине в семестре.
Карта динамики успеваемости студентов по дисциплине
«Математика и математические методы в биологии» 1-я группа (1-й семестр)
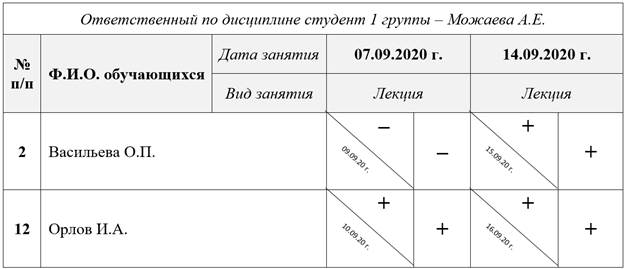
Каждый квадрат разделен условно на две части. В левом нижнем углу указывается дата сдачи задания или восстановления конспекта по пропущенной теме. В верхнем углу квадрата фиксируется оценка или отметка о защите занятия. Справа от каждого квадрата ставится «+» – присутствие на занятии, «–» – отсутствие на занятии. Если студент отсутствовал на лекции, то ответственный по дисциплине ставит перед ним задачу восстановления конспекта в течение нескольких дней, но обязательно до практического занятия по теме лекции. Дату восстановления конспекта, названную студентом, ответственный по дисциплине вносит в левый нижний угол квадрата. Если студент по каким-либо причинам не восстановил конспект или не выполнил задание, то в скобках указывается новая дата сдачи долга.
Организованная таким способом работа учит студентов планировать свою деятельность. В случаях, если обучающийся не выполняет полученное задание в срок, ответственный по дисциплине в группе студент выясняет причины невыполнения и в зависимости от их характера принимает решение о переносе сроков сдачи задания или обращается к преподавателю [14].
Повседневная работа ОДС настраивает студентов на систематическую учебу в течение всего семестра. Карта дает возможность вести целенаправленный диалог с однокурсниками, добиваясь выполнения ими всех заданий в установленный срок. Организованная описанным выше способом работа позволяет решить основную задачу: к сессии студенты оказываются учебно-методически оснащенными, т.е. имеют полный комплект конспектов лекций и не имеют ни одной задолженности по текущей отчетности.
Выполнению поставленных задач способствует также коллективная самостоятельная подготовка, которая действиями ОДС становится более управляемой. В процессе выполнения своей работы он отрабатывает методы, способы, приемы индивидуальной работы со студентами своей группы, учится принимать решения и добиваться их выполнения. Так ответственный по дисциплине студент приобретает организационно-методические навыки, умение побуждать студентов своей группы осмысливать установленные цели и выполнять поставленные задачи. В процессе взаимодействия с однокурсниками ответственный по дисциплине решает шесть профессиональных задач, таких как:
1) обмен информацией (получение и первичная обработка);
2) принятие решений (коммуникационно-управленческий аспект);
3) планирование (целеполагающий аспект, выделение задач);
4) организация (содержательный и процессуальный аспекты);
5) мотивационно-ценностные установки;
6) контроль (рейтинг, диагностика, мониторинг, обработка результатов).
Если ответственный по дисциплине студент не справляется, то он может быть переизбран в любое время, до окончания семестра. Практика исследования показала, что в большинстве случаев было достаточным, что ОДС переизбирались в начале каждого семестра.
Результаты исследования и их обсуждение
Данная модель построения образовательного процесса является одним из элементов повышения качества учебы студентов и развития ими организационно-методических навыков [15]. Анализ результатов освоения дисциплины «Математика и математические методы в биологии» и методики преподавания курса по предложенной модели организации образовательного процесса показал, что:
§ повысилась успеваемость студентов по дисциплине (средний балл группы с назначенным ответственным студентом по дисциплине составил 4,3, средний балл группы без назначенного ответственного студента по дисциплине составил 3,9);
§ способность студентов планировать свою учебную работу в течение семестра значительно улучшилась (по результатам опросов обучающихся, собеседований с ОДС, консультаций с научно-педагогическими работниками, реализующими другие учебные дисциплины (модули, курсы, разделы));
§ организационно-методические навыки студентов совершенствовались от семестра к семестру (по результатам анкетирования обучающихся, принимавших участие в апробации данной модели, консультаций с научно-педагогическими работниками);
§ значительно повысилось качество самостоятельной подготовки студентов (установлено из наблюдений по уменьшению числа студентов, обращающихся за консультацией, и по уменьшению «отрицательных» пунктов в карте динамики успеваемости студентов по дисциплине);
§ наблюдалось повышение качества общей профессиональной математической подготовки обучающихся (по отзывам научно-педагогических работников по другим учебным дисциплинам образовательной программы, которые в той или иной степени пересекаются в своей профессиональной деятельности с элементами математического знания, логическим мышлением, проектной деятельностью, самоорганизацией и т.д.);
§ отмечалось повышение качества общей профессиональной математической подготовки обучающихся (об этом свидетельствуют отзывы научно-педагогических работников по другим учебным дисциплинам образовательной программы, которые в той или иной степени пересекаются в своей профессиональной деятельности с элементами математического знания, логическим мышлением, проектной деятельностью, самоорганизацией и т.д.).
По данной дисциплине была использована балльно-рейтинговая система оценивания. Особенностью данной системы является то, что она обрабатывается в автоматическом режиме с помощью специализированной программной оболочки. В соответствии с разбивкой общего балла за определенный период времени студентам в конце фиксированного среза присуждаются определенные баллы за текущую работу в аудиторное время, коллоквиум, контрольную работу и иные виды активной (творческой, самостоятельной) учебной деятельности. В течение семестра на каждом контрольном срезе наблюдалось качественное отличие результатов успеваемости экспериментальной группы от контрольной на 0,3–0,4 пункта. Впоследствии этот показатель перешел и в результаты экзаменационной сессии, где студенты экспериментальной группы продемонстрировали более качественные ответы.
Повышение успеваемости по математическим курсам отразилось и на успеваемости по дисциплинам, использующим математические выкладки, таким как «Генетика и селекция», «Аналитическая химия», «Биофизика», «Экологическая экспертиза» и др. Студенты групп, по которым был назначен ОДС, легко могли применять математические формулы и методы исследования при решении профессиональных задач по указанным дисциплинам, что, несомненно, является частью общей математической подготовки обучающихся.
Следует отметить, что для ответственного по дисциплине студента со стороны преподавателя есть определенные преференции, поскольку каждодневная работа такого «куратора» должна быть оценена соответствующим образом. Однако практика показала, что ОДС не нуждается в дополнительных поощрениях, так как его «должность» непрерывно держит в тонусе, чтобы всегда быть впереди остальных обучающихся как в профессиональных знаниях по дисциплине, так и в организационно-управленческом, методическом ракурсах. Возложенные на него обязательства обусловливают определенный стиль его обучения и воспитания. По результатам эксперимента можно также заключить, что те студенты, которые долгое время были в статусе ответственного по дисциплине, позднее трудоустроились как в качестве преподавателей, так и в качестве административно-управленческих работников в организациях по профилю обучения и профессиональной подготовки.
Выводы
Таким образом, в процессе реализации данного эксперимента нами были опробованы различные методы и технологии повышения успеваемости студентов и формирования у них организационно-методических навыков. Если проанализировать результаты полученных данных, то можно сделать вывод об эффективности реализуемой нами методики построения образовательного процесса.
Реализация данной модели была возможна и в дистанционном формате, который ввели из-за сложившейся в стране эпидемиологической ситуации. ОДС имели возможность по выделенной образовательной организацией сети дистанционно непрерывно взаимодействовать со своими однокурсниками в онлайн-режиме видео-конференц-связи и проводить консультации, объяснения, проверки, фиксацию исполнения указаний и т.д.
В настоящее время идет подготовка нового этапа в реализации данной модели. Наряду с отслеживанием формирования организационно-методических навыков обучающихся в процессе изучения математических дисциплин будет исследован вопрос педагогического такта и мастерства преподавателя, формирующего указанные навыки и оценивающего успеваемость обучающихся.



