Умение решать текстовые задачи – это одно из главных умений, которое закладывается в начальной школе и позволяет в старших классах применять это умение в новой ситуации. Все типы задач, с которыми ученики сталкиваются в старших классах, берут свое начало в начальной школе. Практически все основные типы и виды задач на движение, на работу изучаются в начальной школе, что является базой для подготовки их к ОГЭ и ЕГЭ.
Проблема, связанная с умением решать задачи, не заканчивается в начальной школе, чаще всего она переходит от рассматриваемой проблемы к потере интереса к обучению. Целью же обучения математике учащихся младших классов является развитие постоянного интереса к изучаемой дисциплине. Интерес можно поддерживать разными способами, предлагая детям решить задачу со сказочным сюжетом, с нестандартной формулировкой, с красочными элементами в задаче, с неожиданными результатами, т.е. постоянно расширяя круг задач и увеличивая их сложность.
Мы знаем, что круг решаемых задач в начальной школе широк, для этого включены все возможности, это и наличие различных обучающих электронных ресурсов, это и возможности внеурочной деятельности, но использование такого типа задач, как на «уравнивание», минимален везде. Но мы знаем, что во многих олимпиадах, в соревнованиях, эти задачи присутствуют. Моделирование же как способ анализа задачи используют многие авторы учебников, этот способ анализа наиболее эффективен. Мы же пытаемся включить в содержание дополнительный материал, он наиболее ярко обобщает применение моделирования в начальных классах при решении задач.
Проведя аналитическую работу, мы собрали большое количество задач и методического материала для использования учителями при обучении математике младших школьников, более того, мы можем говорить о том, что данный материал может быть применен для подготовки детей к олимпиадам.
Одним из показателей обученности в начальной школе является умение анализировать, записывать краткую запись, оформлять решение и ответ к арифметической задаче. К арифметической задаче мы можем приравнять любое задание, в котором есть условие и вопрос. На начальном уровне большие затруднения вызывает анализ условия задачи, а если эта задача логическая, так это еще двойное затруднение. При прохождении педагогической практики многие студенты столкнулись с такой проблемой. Поэтому нами была разработана экспериментальная программа, связанная с решением нестандартных задач с использованием элементов моделирования при составлении краткой записи и решения задач [1].
Умение решать текстовые задачи – это одно из главных умений, которое закладывается в начальной школе. Решение текстовых задач является одним показателей интеллектуального развития младших школьников. Существенным методом для формирования понятия решением текстовой задачи является моделирование.
Элементы моделирования задачи – это подмена действий с реальными предметами действиями с их образцами: моделями, муляжами, макетами, а также с их графическими заменителями: рисунками, чертежами, схемами и т.п. Данными моделями могут быть не конкретные предметы, о которых идёт речь в задаче, а их обобщённые заменители (круги, квадраты, отрезки, точки и т.д.). Для установления отношений и зависимостей между величинами мы используем отрезки в чертеже с некоторым соблюдением масштаба. Если же взаимосвязи передаются приблизительно, без соблюдения масштаба, то работа строится с помощью схематического чертежа.
Удачное применение чертежей, таблиц, схем и рисунков приходит на выручку учащимся в осознанном выявлении невидимых связей между данными и искомыми задачи, но также повышает познавательную активную мыслительную деятельность и учит подбирать наиболее рациональные пути решения задач [2].
Использование моделирования способствует эффективному решению задач. Также моделирование как учебное действие направлено на формирование умственных операций, которые нужны для освоения правил построения и использования моделей в процессе научно-теоретического мышления.
Элементы моделирования являются также основой для воспитания познавательного интереса и самостоятельности, нравственных качеств личности и интеллектуальных задатков при решении простых и нестандартных задач. Включение нетрадиционных задач в учебную деятельность младших школьников способствует возникновению интереса к решению задач лишь тогда, когда у них появляется устойчивая потребность довести это решение до логического завершения, получить результат. Также интересы младших школьников к данным задачам объясняются интересом к яркой занимательной формулировке данных задач. Занимательность зачастую представляется в виде приключений, неожиданных событий, которые часто отвлекают от сути задач. Задачам с нетрадиционной формулировкой характерна отвлеченность, необычность изложения и хода решения, которая нам дает возможность довести любопытство ребенка до учебного интереса, что позволяет учителю использовать детскую любознательность в обучении. Удивление и интерес учеников могут быть направлены уже на весь комплекс приемов, возможных способов решения задач, на их многообразие оформления условия и решения [3].
Нами был проведен эксперимент с учениками 2 «Е» класса МБОУ «СОШ № 27» города Чебоксары. Учитывая возрастные особенности учеников, мы подобрали комплекс нестандартных задач на уравнивание. Решение таких задач вызывает затруднения у детей младшего школьного возраста. Чтобы избежать этого, мы использовали при решении таких задач прием моделирования. Подготовка проходила в несколько этапов.
Например, на первом этапе мы познакомили учащихся с решением следующего вида задач [4]: «1 чашка и 1 блюдце стоят 9 рублей. Сколько стоят 3 чашки и 3 блюдца».
При оформлении краткой записи ученикам порекомендовали использовать геометрические фигуры, такие как четырехугольник и круг, для обозначения предметов. На доске также показывается схема задачи.

На этом этапе дети учатся выделять пары предметов и находить общую стоимость посредством сложения этих пар.
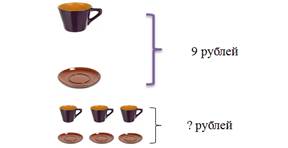
На втором этапе учащиеся уже выделяют недостающие предметы в парах и стоимость каждого предмета в одной паре, например: «Яблоко и груша вместе стоят 11 рублей. А 5 яблок и 3 груши стоят 45 рублей. Сколько стоит одно яблоко и одна груша в отдельности?»
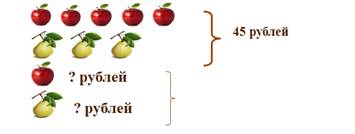
При разборе задачи учащимся необходимо задавать такие вопросы, например:
- Сколько пар фруктов мы можем выделить из 5 яблок и 3 груш?
- А сколько яблок еще остается?
- Как мы найдём, сколько стоит одно яблоко?
- А как можем найти, сколько стоит груша?
Посредством вышеизложенных вопросов дети приходят к выводу, что стоимость одного предмета, который не имеет пару, можно найти, выделив пары предметов из числа данных.
Аналогичным образом учащиеся решают следующий тип задач.
Яблоко и груша вместе стоят 11 рублей. А 5 яблок и 3 груши стоят 45 рублей. Сколько стоит одно яблоко и одна груша в отдельности?
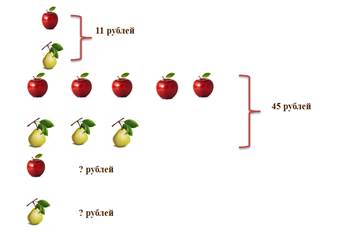
При разборе задачи учащимся необходимо задавать такие вопросы:
- Сколько пар фруктов мы можем выделить из 5 яблок и 3 груш?
- А сколько яблок еще остается?
- Как мы найдём, сколько стоит одно яблоко?
- А как можем найти, сколько стоит груша?
Также на этом этапе рассматривается следующая задача.
4 пуговицы и 3 булавки стоят 31 рубль, 2 пуговицы и 2 булавки – 18 рублей. Сколько стоит 1 пуговица и 1 булавка по отдельности?
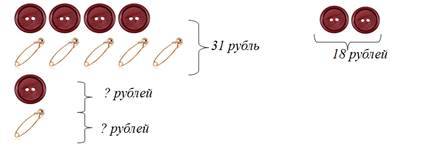
При решении задач такого вида дети в начале разбора определяют, сколько стоит одна пара предметов, затем узнают, какое количество пар предметов содержится в данной группе, после этого находят цену предмета, который не имеет пары. Также при разборе данной задачи рекомендуется задавать такие вопросы:
- Как можем узнать, сколько стоит одна пара предметов?
- Сколько пар предметов мы можем выделить из 4 пуговиц и 3 булавок?
- Сколько еще пуговиц остается?
- Как мы найдем, сколько стоит одна пуговица и сколько стоит одна булавка?
Третий этап эксперимента предполагает прочное усвоение этапов решения такого вида задач. Это способствует закреплению умения видеть пары предметов в различных группах, то есть соотнести данные предметы между собой и выделить недостающие предметы. Также на этом этапе учащиеся соотносят недостающие предметы в двух группах, определяют общее количество предметов и находят величину каждого предмета [5]. Например: «3 поросенка и 2 ягненка весят 37 кг, а 2 поросенка и 3 ягненка весят 48 кг. Сколько весит поросенок и сколько весит ягненок?»
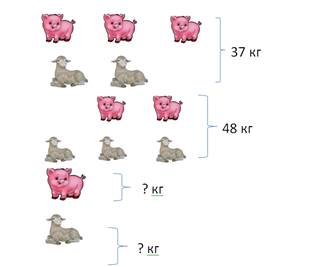
На этом этапе целесообразно подвести учеников к решению задачи следующими вопросами:
- Сколько всего пар мы можем выделить из первой группы? Сколько можем выделить из второй?
- А сколько всего пар можно выделить из двух групп? Как мы это найдем?
После того как учащиеся находят, сколько пар предметов в обеих группах, они приходят к выводу, что можно найти, сколько стоит одна пара. Затем учащиеся уже находтят стоимость одного предмета в одной группе, который не имеет пары, путем вычитания суммы стоимости выделенных пар от общей стоимости всех предметов в этой группе.
Такие виды задач формируют у учащихся творческое воображение, логическое мышление и умение составлять краткую схему задачи. Целью данного эксперимента является научить учеников начального класса решать данного рода задачи с использованием элементов моделирования.
Мы пришли к выводу, что элементы моделирования могут быть одним из эффективных средств поиска решения задачи. Для того чтобы построить модель к задаче и использовать ее при преобразовании, нужно детей научить находить в условии задачи главную цель, а также все данные величины и их зависимости, с возможностью исключения несущественных связей. Это позволит провести подробный анализ, с помощью которого можно найти решение задачи [6].
Рекомендуется использовать такие виды заданий с применением моделирования для закрепления пройденного материала:
· По данной модели составь задачу.
· Дан текст задачи. Построить ее модель. Какие разные модели можно построить для этой задачи?
· Запиши (зарисуй) этапы работы над …
· Можешь ли в другой форме представить модель (схему)?
· Попробуй создать модель (схему), которая поможет тебе понять способ решения.
· Кто понял, какая идея мысль предложена в этой модели (схеме)?
· Как показать в схеме свойства …
· Начерти (дополни) схему, соответствующую заданию.
Вопросы для проверки схемы (модели) текстовых математических задач:
· Все ли величины отражены?
· Все ли числовые данные представлены?
· Соблюдены ли отношения между величинами?
· Обозначена ли искомая величина?
· Нет ли лишнего в схеме?
Данные вопросы можно использовать при работе со всеми видами задач, изучаемыми в начальной школе.



