Роль математики в выборе старшеклассниками профессий технического и экономического профилей сложно переоценить. Традиционно считается, что математика нужна для приобретения привычки анализировать информацию, логически рассуждать и четко формулировать свои мысли. Однако такая мотивация недостаточна для современных школьников, она слишком расплывчата и, как правило, не доходит до сознания обучающегося. Необходимы более конкретные и понятные аргументы. И эти аргументы, прежде всего, должны быть тесно связаны с его будущей профессией, с которой он тоже знаком лишь поверхностно. Слова о том, что без математики сложно обойтись в век информации и информационных технологий, должны быть подкреплены четкими и простыми примерами. Обучающийся должен увидеть, что математика является тем необходимым инструментом, который можно применить при решении не только проблем в области современных информационных технологий, но и многих социально-экономических задач.
Целью нашего исследования являлось выявление возможностей использования математических задач с экономическим содержанием в профориентационной работе с обучающимися.
Материалы и методы исследования. В Лесосибирском филиале Сибирского государственного университета науки и технологий имени академика М.Ф. Решетнева неоднократно проводились мероприятия, направленные на профориентацию школьников [1]. В 2020 г. нами была проведена серия командных состязаний в рамках интеллектуального марафона «ПрофиМатика». Командные состязания проходили по информатике и экономике среди обучающихся 10–11-х классов школ города. Старшеклассникам предлагалось решить 10 задач с экономическим содержанием, относящихся к разным типам: задачи на проценты (в том числе сложные), задачи на использование функций и их производных. На решение каждой задачи отводилось от 2 до 10 мин, в зависимости от сложности вычислений. Рассмотрим некоторые из предложенных задач.
Задачи на проценты. Понятие процента широко используется в экономических задачах разного типа. Большинство таких задач решаются достаточно легко. Например, если какая-либо величина 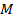 увеличивается на
увеличивается на 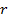 процентов, то результат такого увеличения будет:
процентов, то результат такого увеличения будет:
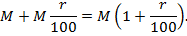
При уменьшении величины 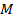 на
на 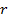 процентов:
процентов:
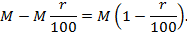
При решении задач на кредиты и вклады данный метод расчета получил название «формулы простого процента»:
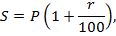
где 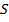 – наращенная сумма,
– наращенная сумма, 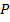 – первоначальная сумма,
– первоначальная сумма, 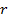 – годовая процентная ставка.
– годовая процентная ставка.
Большую сложность представляет решение задач на использование сложного процента («процент от процента») [2]. Для его вычисления используется следующая формула:
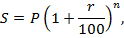
 – количество начислений за период.
– количество начислений за период.
Рассмотрим несколько примеров задач на проценты.
Задача 1. Цена некоторого товара вначале увеличилась на 10%, а затем на 10% уменьшилась. Как изменилась цена товара по сравнению с первоначальной?
Ошибочно считать, что цена в обоих случаях одинакова. После подорожания цена товара составила 110%, или 1,1 от первоначальной цены, а после удешевления – 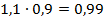 , т.е. 99% от первоначальной. Значит, после снижения цены товар стал на 1% дешевле, чем до подорожания.
, т.е. 99% от первоначальной. Значит, после снижения цены товар стал на 1% дешевле, чем до подорожания.
Многие задачи на проценты очень легко и наглядно решаются с помощью пропорций. Покажем это на примере следующей задачи.
Задача 2. Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Вера Николаевна получила 39 150 руб. Сколько рублей составила заработная плата Веры Николаевны?
Пусть  – зарплата Веры Николаевны до удержания налога, которой соответствуют 100%. Тогда зарплате 39 150 руб. соответствуют
– зарплата Веры Николаевны до удержания налога, которой соответствуют 100%. Тогда зарплате 39 150 руб. соответствуют 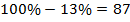 % и получаем следующую пропорцию:
% и получаем следующую пропорцию:
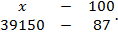
Значит, 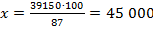 руб.
руб.
Задача 3. Прибыль предприятия в 2017 г. составила 2 млн руб. Каждый следующий год прибыль увеличивалась на 300% по сравнению с предыдущим годом. Какую прибыль предприятие будет иметь в 2020 г.?
По формуле сложного процента рассчитаем прибыль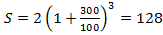 млн руб.
млн руб.
Задача 4. Банк предлагает клиентам открыть два вклада сроком на 1 год: обычный и с капитализацией. Вклад «Счастливая десятка» размещается под 10% годовых, проценты начисляются в конце срока вклада. Вклад «Счастливый месяц» размещается под 9,8% годовых, проценты по вкладу капитализируются (причисляются к сумме вклада) каждый месяц. Какой из этих вкладов выгоднее?
Определим накопленную сумму первого вклада 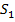 по формуле простых процентов
по формуле простых процентов
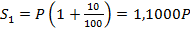 ;
;
а накопленную сумму второго вклада 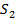 по формуле сложных процентов:
по формуле сложных процентов:
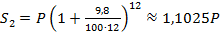 .
.
Откуда делаем вывод, что второй вклад выгоднее первого.
Задачи с использованием функций и их производных. Понятие функции – одно из основных в математике. Оно выражает зависимость одних переменных величин от других. В экономике функции используются в качестве моделей при анализе экономических процессов. Наиболее часто в экономике применяются следующие функции [3]:
– функция полезности или предпочтений, т.е. зависимости полезности (результата) некоторого действия от уровня (интенсивности) этого действия;
– производственная функция – выражает зависимость результата производства от обусловивших его факторов (функция выпуска продукции, функция издержек, функция спроса, функция предложения).
Задача 5. Продавец предусмотрел возможность получения оптовой скидки, размер которой зависит от количества покупаемого товара. Так, при покупке партии товара в количестве менее 100 штук цена будет 300 руб. за штуку; от 100 до 1000 штук – 280 руб.; более 1000 штук – 250 руб. Определить функцию стоимости произвольной партии товара от цены 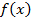 и рассчитать стоимость партии из 800 штук.
и рассчитать стоимость партии из 800 штук.
Зададим функцию стоимости партии товара в следующем виде:
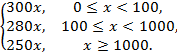
Определим стоимость партии товара из 800 штук, используя вторую формулу системы:
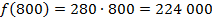 руб.
руб.
Задача 6. Функция предложения товара описывается как 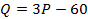 , где
, где 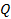 – количество, в штуках, а
– количество, в штуках, а 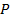 – их цена, в долл.; функция спроса имеет вид
– их цена, в долл.; функция спроса имеет вид 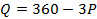 . Определить равновесную цену (Ре) и равновесный объем продаж (Qe) аналитическим и графическим способами.
. Определить равновесную цену (Ре) и равновесный объем продаж (Qe) аналитическим и графическим способами.
При решении таких задач, прежде всего, должно быть понимание экономической сущности рыночного равновесия и его параметров – равновесной цены и равновесного объема (количества).
Равновесной ценой называется такая цена, при которой объемы спроса и предложения равны. Поэтому для ее определения приравниваем правые части уравнений функций:
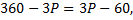
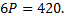
Следовательно, 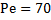 долл.
долл.
Определим равновесный объем, подставив равновесную цену в любую из заданных функций: 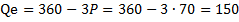 штук.
штук.
Таким образом, аналитически было определено, что при установлении рыночной цены 70 долл. количество товара, на который предъявят спрос покупатели, и количество, которое будет предложено на продажу производителями, составит 150 штук, т.е. будет наблюдаться равновесие.
Графическое решение данной задачи сводится к построению графиков функций, кривых спроса и предложения и определению координат их точки пересечения. Традиционно в экономике при построении кривых спроса и предложения независимую переменную – цену товара (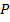 ) – откладывают по вертикальной оси координат, а значения функций спроса и предложения (
) – откладывают по вертикальной оси координат, а значения функций спроса и предложения (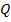 ) – по горизонтальной.
) – по горизонтальной.
Построенные по заданным функциям графики представлены на рисунке 1. Искомой точкой равновесия является точка с координатами (150; 70). Это означает, что при цене, равной 70, объемы спроса и предложения равны 150, т.е. по этой цене весь представленный товар найдет своего покупателя и все желающие купить товар по данной цене будут иметь возможность это сделать.
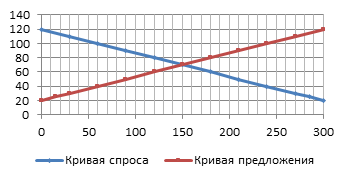
Рис. 1. Кривые спроса и предложения
Более сложными для школьников являются задачи, требующие в своем решении нахождения производной функции. Такая необходимость может возникнуть, например, в следующих случаях:
– при расчете показателей эластичности функции;
– при определении оптимальных экономических результатов (объема выпуска, цены, процента), в том числе в условиях ресурсного ограничения.
Понятие эластичности функции широко используется в исследовании чувствительности спроса к изменению определяющих его факторов. Эластичность показывает, на сколько процентов изменится функция при изменении независимой переменной на 1%. Если предполагается, что эти изменения ничтожно малы, то используют точечный способ расчета эластичности функции.
Рассмотрим пример задачи на расчет ценовой эластичности спроса.
Задача 7. Предположим, что функция спроса на товар задана следующим уравнением: 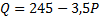 . Какова эластичность спроса по цене 10 руб.?
. Какова эластичность спроса по цене 10 руб.?
В решении задачи необходимо использовать формулу точечной эластичности спроса по цене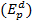 :
:
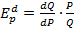 ,
,
где 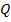 – объем спроса;
– объем спроса; 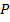 – цена.
– цена.
Степень изменения объема спроса при изменении цены находится путем вычисления первой производной функции спроса:
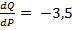 .
.
Найдем объем спроса при цене 10: 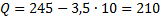 .
.
Подставим найденные значения в формулу точечной эластичности спроса:
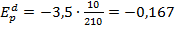 .
.
Найденное значение –0,167 говорит о том, что если цена товара изменится на незначительную величину, то величина спроса изменится в противоположном направлении, примерно на 0,167%.
Задачи на оптимальный выбор сводятся к нахождению экстремальных (минимальных или максимальных) значений некоторой функции. Точки, в которых функция принимает экстремальные значения, определяются с помощью производной [4]. Наиболее часто можно встретить задачи на определение оптимального объема производства, при котором прибыль максимальна.
Задача 8. Фирма производит 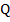 единиц продукции. Доходы считаются по формуле
единиц продукции. Доходы считаются по формуле 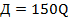 , а расходы –
, а расходы – 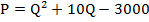 . При каком значении
. При каком значении 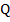 прибыль будет максимальной? Найдите эту максимальную прибыль.
прибыль будет максимальной? Найдите эту максимальную прибыль.
Для определения оптимального объема производства, при котором прибыль (П) будет максимальна, необходимо определить производную прибыли и приравнять ее к нулю.
Прибыль – это разница доходов и расходов. Поэтому функция прибыли будет иметь вид:
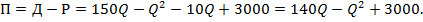
Для нахождения максимума данной функции нужно вычислить ее производную и приравнять к нулю:
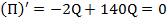 ,
,
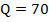 .
.
Графический способ решения предполагает определение объема через определение вершины параболы по формуле: 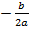 .
.
В нашем случае получаем 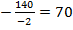 .
.
Далее определяем размер прибыли, подставляя найденное значение объема в функцию прибыли:
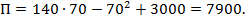
Задачи с ресурсными ограничениями представляют собой задания на нахождение максимального выпуска при ограничениях затрат по любому виду ресурса (труд, материалы, сырье и т.д.). Рассмотрим в качестве примера задачу, в которой ограничительным фактором выступают затраты на оплату труда.
Задача 9. Компания осуществляет производство изделия по одинаковой технологии на двух заводах, расположенных в разных регионах. На каждом из заводов месячный объем производства 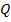 равен
равен 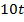 изделий, если рабочие трудятся
изделий, если рабочие трудятся 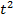 часов в месяц. Часовая оплата труда на одном заводе составляет 400 руб., а на другом – 500 руб. Компания может использовать на оплату труда в месяц не более 28 800 000 руб. Определить максимальный объем производства на двух заводах.
часов в месяц. Часовая оплата труда на одном заводе составляет 400 руб., а на другом – 500 руб. Компания может использовать на оплату труда в месяц не более 28 800 000 руб. Определить максимальный объем производства на двух заводах.
Представим рабочее время в часах за месяц на первом заводе как 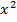 , а на втором – как
, а на втором – как  . Тогда объем производства на первом заводе равен
. Тогда объем производства на первом заводе равен 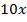 , а на втором заводе –
, а на втором заводе – 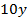 . Затраты на оплату труда (
. Затраты на оплату труда (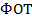 ) компании представим как сумму заработной платы рабочих на первом и втором заводах:
) компании представим как сумму заработной платы рабочих на первом и втором заводах:
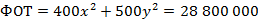 .
.
После преобразования получим:
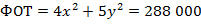 ,
,
откуда 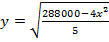 .
.
Cоставим функцию объема производства 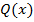 :
:
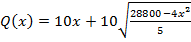 .
.
Найдем наибольшее значение данной функции, приравняв производную функции к нулю:
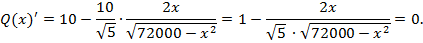
Производная функции 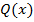 будет равна нулю, если
будет равна нулю, если 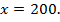 В этом случае
В этом случае 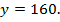 Следовательно, искомый максимальный объем производства на двух заводах составит:
Следовательно, искомый максимальный объем производства на двух заводах составит: 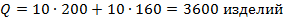 .
.
Результаты исследования и их обсуждение. Рассмотренные выше задачи были предложены для решения пяти различным командам обучающихся 10-х классов. Ни одна из команд не справилась полностью с решением всех задач. Лучшим результатом было решение девяти из десяти представленных задач, худшим – пяти из десяти задач. Наименьшую сложность у школьников вызвали задачи на простые проценты, с ними справились все команды. В то же время при решении задач на сложные проценты возникли трудности, связанные с недостаточным пониманием как процента, так и сути экономического явления, описываемого в ситуации. Основные сложности в решении задач с построением функции и вычисления ее производной заключались в неспособности применить математическую теорию к конкретной экономической ситуации.
Заключение. Игры в рамках интеллектуального марафона «ПрофиМатика» вызвали живой интерес у обучающихся, подтвердив тем самым правильность выбора формата мероприятия, и, поскольку математика обладает большим потенциалом для повышения интереса к различным профессиям, в том числе экономического профиля [5], были полезны им с точки зрения профессионального самоопределения.
Работа выполнена при поддержке Красноярского краевого фонда поддержки научной и научно-технической деятельности (конкурс по организации проведения мероприятий по профессиональной ориентации молодежи, код заявки: 2020013005781).



