Последние годы процесс информатизации образования набирает все большие обороты. Этот процесс обуславливает создание новых технологий и методических систем обучения, направленных на совершенствование интеллектуального потенциала обучаемого, на формирование умений самостоятельно приобретать знания, осуществлять учебную, исследовательскую деятельность, а также различные виды самостоятельной деятельности. Все это требует совершенствования методологии отбора содержания, средств, методов и организационных форм обучения [1]. В полной мере все указанные аспекты относятся и к математической подготовке будущих инженеров.
Цель исследования: на примере курса «Дифференциальные уравнения» для будущих инженеров в цифровой образовательной среде NOMOTEX (ЦОС NOMOTEX) показать основные принципы отбора содержания обучения, а также особенности проведения семинарских и лекционных занятий.
Материал и методы исследования
Курс «Дифференциальные уравнения» в ЦОС NOMOTEX начал разрабатываться и одновременно внедряться в процесс обучения в 2018-2019 учебном году. В течение весеннего семестра он был апробирован на факультете энергетического машиностроения МГТУ им. Н.Э. Баумана и аэрокосмическом факультете для бакалавров, обучающихся по направлению подготовки 20.03.01 «Техносферная безопасность», и специалистов, обучающихся по специальностям 16.05.01 «Специальные системы жизнеобеспечения», 14.05.01 «Ядерные реакторы и материалы».
В весеннем семестре 2019-2020 учебного года курс был внедрен в процесс дистанционного обучения.
Структура курса
В ЦОС NOMOTEX курс представлен в виде нейросетевой структуры знаний (рис. 1).
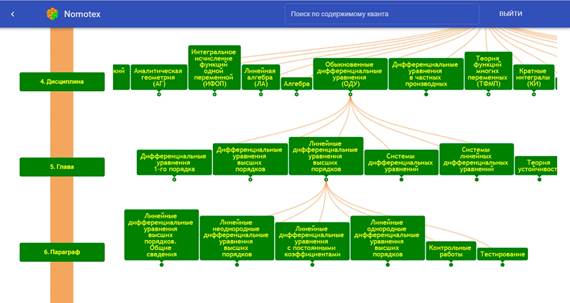
Рис. 1. Нейросетевая структура знаний (дерево)
Содержание курса традиционно разбито на главы и параграфы.
Глава 1. Дифференциальные уравнения первого порядка.
Общие сведения о дифференциальных уравнениях.
Обыкновенные дифференциальные уравнения первого порядка.
Глава 2. Дифференциальные уравнения высших порядков.
2.1. Уравнения, допускающие понижение порядка.
Глава 3. Линейные дифференциальные уравнения высших порядков.
3.1. Линейные дифференциальные уравнения высших порядков. Общие сведения.
3.2. Линейные однородные дифференциальные уравнения высших порядков.
3.3. Линейные неоднородные дифференциальные уравнения высших порядков.
3.4. Линейные дифференциальные уравнения с постоянными коэффициентами.
Глава 4. Системы дифференциальных уравнений.
4.1. Нормальные системы дифференциальных уравнений.
Глава 5. Системы линейных дифференциальных уравнений.
5.1. Системы линейных однородных дифференциальных уравнений.
5.2. Системы линейных неоднородных дифференциальных уравнений.
5.3. Системы линейных дифференциальных уравнений с постоянными коэффициентами.
Внутри каждого параграфа содержание представлено в виде так называемых квантов – единиц знаний [2-4] (рис. 2).
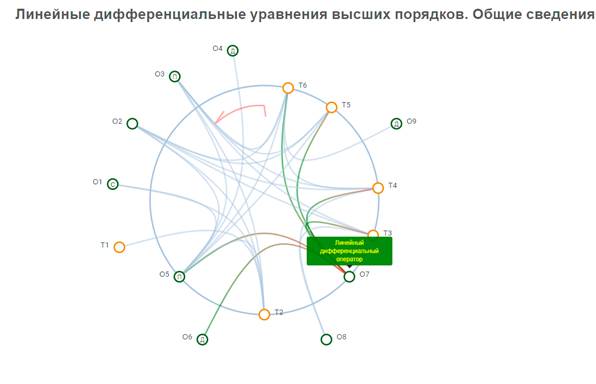
Рис. 2. Содержание параграфа
В квантах содержатся определения (О), теоремы (Т), свойства (Св), а также методы решения задач – квант «построение» (П). Все кванты текущего параграфа расположены на окружности. Вне окружности расположены кванты из других глав и курсов, связанные тем или иным образом с содержанием данного параграфа. Показаны связи между представленными квантами.
Структура и содержание кванта
Каждый квант графически представлен в виде «светофора» - трех окон зеленого, желтого и красного цвета (рис. 3).

Рис. 3. Содержание кванта
В определении математического понятия в первых двух окнах содержится совокупность условий, необходимых и достаточных для выделения классов объектов, принадлежащих этому понятию, а в красном – название понятия.
Пример 1. Квант «Фундаментальная система решений линейного однородного дифференциального уравнения» (О)
 Рассмотрим линейное однородное дифференциальное уравнение n-го порядка
Рассмотрим линейное однородное дифференциальное уравнение n-го порядка
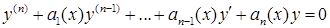 ,
,

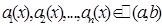 .
.
Совокупность любых n линейно независимых на интервале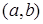 решений
решений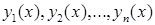 этого уравнения
этого уравнения
 называется фундаментальной системой решений (ФСР) на интервале
называется фундаментальной системой решений (ФСР) на интервале 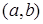 .
.
Теоремы сформулированы не в категоричной, а в условной форме. В первых двух окнах содержится условие теоремы, в третьем – ее заключение.
Пример 2. Квант «Теорема о структуре общего решения линейного однородного дифференциального уравнения n-го порядка» (Т)
 Рассмотрим линейное однородное дифференциальное уравнение n-го порядка
Рассмотрим линейное однородное дифференциальное уравнение n-го порядка
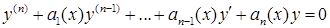 ,
,

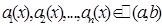 .
.
Если 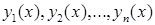 - какая-либо фундаментальная система решений этого уравнения на интервале
- какая-либо фундаментальная система решений этого уравнения на интервале 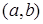 , то
, то
 общим решением этого уравнения на интервале
общим решением этого уравнения на интервале 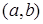 является линейная комбинация
является линейная комбинация
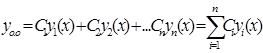 ,
,
где 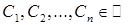 - произвольные коэффициенты.
- произвольные коэффициенты.
В отдельных окнах содержатся доказательства теорем, следствия, замечания, геометрические иллюстрации, математические примеры и задачи, подобранные к данному кванту.
Отметим удобную систему ссылок, расположенных в содержании кванта, позволяющих в всплывающих окнах видеть необходимую информацию из всей представленной базы знаний, а также возможность пошагового режима презентации изложенного в кванте материала.
Уникальность ЦОС NOMOTEX состоит в том, что она дает возможность проведения всех видов аудиторной и самостоятельной работы со студентами.
В процессе обучения математическим дисциплинам в ЦОС NOMOTEX наиболее сильные изменения претерпевает лекционное занятие. Традиционно лекция – систематическое последовательное изложение преподавателем учебного материала, как правило, теоретического характера. Основной дидактической целью лекции является необходимость дать студентам современные, целостные, взаимосвязанные знания. Это отражает отечественную традицию фундаментальности образования. Чтение лекций с использованием ЦОС NOMOTEX сопровождается показом на интерактивной доске необходимого теоретического материала, собранного в единой базе знаний и выделенного в отдельно взятую лекцию с помощью опции «реализация нейросетевых образовательных программ» [5] (рис. 4).
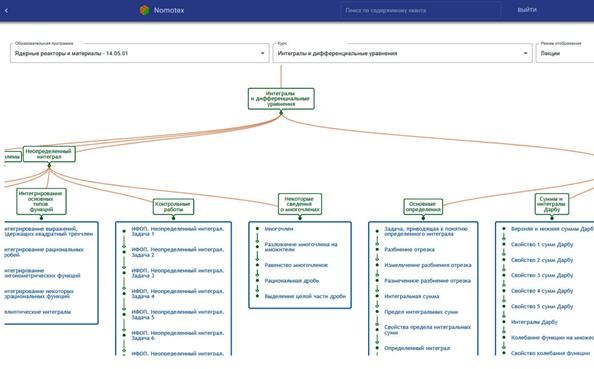
Рис. 4. План лекций по дисциплине «Интегралы и дифференциальные уравнения»
У студентов есть возможность использовать на занятиях собственные ноутбуки, планшеты, а также работать с мобильной версией ЦОС NOMOTEX и, что очень важно, продолжать начатую на лекции работу дома.
Помимо этого, у преподавателя остается возможность в ходе лекции пользоваться доской и мелом.
Семинары также проходит в специализированных аудиториях. В ЦОС NOMOTEX представлены алгоритмы решения стандартных задач. Каждый семинар снабжен большим количеством разобранных примеров и задач для самостоятельной работы (рис. 5).

Рис. 5. Пример задачи для работы на семинаре
Контрольные мероприятия также проводятся в ЦОС. Выдача билетов для контрольного мероприятия, проверка выполненных работ, рейтинг учащихся доступны преподавателю через сервис «личный кабинет» (рис. 6).
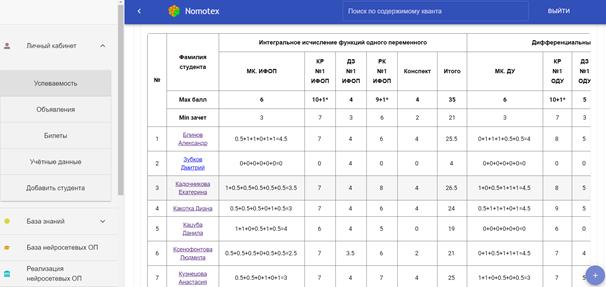
Рис. 6. Рейтинг учебной группы в личном кабинете преподавателя
Заключение
Представленный курс «Дифференциальные уравнения» полностью снабжен теоретическим материалом, составляющим содержание обучения, объемным банком заданий для семинарских занятий, самостоятельной работы, контрольных мероприятий. Существует возможность автоматизированной проверки результатов работы студентов, система интегрирована в модульно-рейтинговую систему обучения университета.
ЦОС NOMOTEX позволяет реализовывать различные курсы, формируя содержание лекций и семинарских занятий из имеющегося банка знаний.
Обучение с использованием представленной цифровой образовательной среды в течение двух лет показало эффективность, в том числе и во время полного перехода на дистанционное обучение.
В дальнейшем планируется расширить курс с целью его внедрения в процесс обучения бакалавров по направлению подготовки 02.03.01 «Математика и компьютерные науки», добавив дополнительные параграфы в имеющиеся главы, а также новую главу «Теория устойчивости». Также планируется насыщение курса, пополнение банка заданий, визуализация квантов инженерными примерами и задачами.



