В настоящее время общепринято мнение, что к математической подготовке конкурентоспособных профессионалов аграрного профиля следует подходить с позиций прикладной профильной направленности при изучении фундаментальных математических понятий. Под прикладной профильной направленностью С.П. Шмалько понимает обучение, при котором реализуется связь математики с дисциплинами профессиональной направленности на разных уровнях, когда идет непрерывный процесс овладения студентами приемами и методами освоения своей будущей профессии [1, с. 76]. Для данного обучения разработаны концепции, принципы и подходы, интегрирующие научные знания о реализации профильной направленности в курсе математики (в частности, линейно-концентрическая модель построения содержания и средств обучения профильно ориентированного курса [2, с. 4]). Анализ внедрения показал, что ожидаемый эффект от этих инновационных разработок можно увеличить, если будет решена проблема восприятия учебных математических текстов сложной понятийной структуры, изобилующих специальными терминами, второстепенной информацией. Именно такими текстами являются профильные задачи по математике, описывающие проблемные ситуации из будущей профессиональной деятельности студентов и решаемые специальными математическими средствами и методами.
При анализе процесса понимания учебной информации в профильной задаче авторы обращались к категориям философской герменевтики [3], к исследованиям «структуры понимания» применительно к процессу обучения математике в высшей школе [4], опирались на применение герменевтического подхода при создании и использовании учебных материалов в обучении математике [5-7]. В результате была предложено особое структурирование профильной задачи, соответствующее траекториям движения мысли по герменевтическому кругу [8, с. 6]: от расширения применения математического понятия к углублению понимания этого понятия. При этом построение математической модели ситуации, описанной в задаче, было достигнуто постепенно: по виткам герменевтического круга, при неоднократном возвращении к более глубокому осознанию математической теории.
Цель исследования: внедрить в обучение и экспериментально проверить эффективность организации процесса понимания профильной задачи, структурированной с применением указанного герменевтического подхода.
Материал и методы исследования. Площадкой для проведения исследования являлся Кубанский государственный аграрный университет имени И.Т. Трубилина, факультеты: «Агрономический», «Агрохимия и защита растений», «Плодоовощеводство и виноградарство». В качестве контрольной и экспериментальной групп были выбраны параллельные группы с одного потока, примерно одинаковой успеваемости. На лекции обе группы студентов были ознакомлены с профильным смыслом изучаемых математических понятий и примерами их применения в сельскохозяйственной практике. На практических занятиях в экспериментальной группе содержание профильных задач было структурировано согласно предложенной концепции. Таким образом, обучаемые входили в герменевтический круг связей и соотношений профильной задачи – от первичных представлений о математическом понятии до его приложений в окружающем мире. Контрольная группа с данным структурированием не была ознакомлена. Экспериментальная работа проведена на материале темы «Дифференциальное исчисление функции одной переменной» зимой 2019–2020 г. с использованием двух способов получения данных.
1-й способ – анкетирование, которое охватило 124 обучаемых. Оно позволило выявить их отношение к прикладной профильной направленности курса в целом и к структурированию профильной задачи в контексте герменевтического подхода в частности.
2-й способ – оценка выполнения контрольной работы. Способ позволил констатировать статистически достоверные сдвиги, характеризующие уровень освоения предложенной темы в экспериментальной группе по сравнению с контрольной.
Для сопоставления данных применялись следующие способы.
1. Визуально-аналитические способы сопоставления (диаграммы и таблицы), в которых наглядно демонстрируются различия в изучаемом признаке. Использовалась методика, описанная в [9, с. 122].
2. Расчетно-аналитические способы проверки статистических гипотез, в частности угловое преобразование Фишера. Этот многофункциональный критерий рекомендуется в педагогических исследованиях для сопоставления результатов двух небольших выборок как по качественному, так и по количественному признаку, а также по уровню и распределению производимого эффекта. Оценивает достоверность различий между процентными долями этих выборок [10, с. 2].
Статистические данные обрабатывались с помощью табличного процессора Excel.
Результаты исследования и их обсуждение. В таблице представлено распределение ответов на вопросы анкеты по указанным вариантам отдельно для экспериментальной и контрольной групп. На последние два вопроса анкеты отвечали только участники экспериментальной группы (59 человек из 124) как ознакомленные с подлежащим проверке подходом к решению задач.
Результаты анкетирования студентов
|
Вопрос анкеты |
Ответы по категориям, % экспериментальная группа / контрольная группа |
|||
|
|
«да» |
«скорее да, чем нет» |
«скорее нет, чем да» |
«нет» |
|
1. Необходимо ли при изучении математики ориентироваться на методы ее применения в будущей профессии? |
49,1 / 55,4 |
33,9 / 35,4 |
13,5 / 7,7 |
3,5 / 1,5 |
|
Итого в среднем |
86,9 |
13,1 |
||
|
2. Считаете ли, что профильные задачи повышают интерес к изучению математики у студентов агробиологических факультетов? |
40,7 / 44,6 |
27,1 / 32,3 |
25,4 / 13,8 |
6,8 / 9,3 |
|
Итого в среднем |
72,35 |
27,65 |
||
|
3. Устраивает ли вас организация профильной направленности в виде предложенных профильных задач по математике? |
69,5 / 52,3 |
22,0 / 32,3 |
6,8 / 12,3 |
1,7 / 3,1 |
|
Итого в среднем |
87,9 |
12,1 |
||
|
4. Считаете ли вы, что предложенные задачи способствуют эффективному освоению данной учебной темы? |
50,8 / 64,6 |
45,8 / 27,7 |
3,4 / 7,7 |
0 / 0 |
|
Итого в среднем |
94,4 |
5,6 |
||
|
5. Является ли легкой для восприятия (понимания) математическая задача, сформулированная в специальных терминах? |
25,4 / 12,3 |
18,6 / 10,7 |
33,9 / 40,0 |
22,1 / 36,9 |
|
Итого в среднем |
33,5 |
66,5 |
||
|
6. Предложенное структурирование позволяет лучше понимать и решать профильные задачи? |
66,1 / – |
30,5 / – |
3,4 / – |
0 / – |
|
Итого в среднем |
96,6 |
3,4 |
||
|
7. После предложенного структурирования стало легче понимать и решать обычные математические задания? |
57,6 / – |
39,0 / – |
3,4 / – |
0 / – |
|
Итого в среднем |
96,6 |
3,4 |
||
Данные таблицы показывают, что по всем вопросам анкеты, кроме пятого, имелось подавляющее большинство положительных ответов («да» и «скорее да, чем нет», что соответствует «высоко» или «высоко в целом, но отмечаю недостатки»). В среднем 86,9% респондентов считают необходимым проведение профильной ориентации обучения посредством применения математики в сфере их будущей профессиональной деятельности. Чуть меньше опрошенных отводят профильным задачам важную роль в усилении интереса к математике у обучающихся агробиологических специальностей. Снижение процента ответов в этом вопросе объясняется «синдромом тревожности», который возникает, как только приходится отходить от стандартных математических заданий в сферу составления математических моделей проблемной ситуации в агробиологической сфере. 87,9% студентов положительно рассматривают организацию профильной направленности обучения в виде предложенных профильных задач. 94,4% респондентов считают, что предложенные задачи способствуют эффективному освоению данной учебной темы. Если сравнивать отдельно показатели контрольной и экспериментальной групп, то число положительных ответов на вопросы 1–4 у них отличается не более чем на 10%.
Ответы на пятый вопрос ясно показывают, что для большинства анкетируемых обеих групп математические задачи, сформулированные в профессиональных терминах, не являются легкими для восприятия. В этом мнении доля студентов экспериментальной группы даже превысила данные контрольной группы (77% против 56%). Это объясняется тем, что в экспериментальной группе такие задачи изучены более подробно и глубоко, обучаемым знакомы их специфика и многосложность. Разработанное для решения этой проблемы структурирование в виде совокупности герменевтических связей позволило подавляющему большинству (около 96,6% студентов) лучше понимать и решать как профильные, так и обычные задачи.
Итак, анализ результатов анкетирования подтвердил выдвинутые ранее предположения о важности профильной ориентации курса в виде профильных задач, о сложности восприятия таких задач и положительной роли герменевтического структурирования для их решения.
Успешность восприятия напрямую связана с верным математическим решением профильной задачи, так как понимание приводит к верной интерпретации специальных профессиональных терминов и соотношений в математические выражения. Поэтому была проведена контрольная работа, состоящая из пяти заданий. Номера 1, 2, 3 контрольной работы представляли собой традиционные для данной темы математические задания. Профильные задачи под номерами 4, 5 подбирались достаточно простыми, например: «Задан закон накопления сухой биомассы винограда в зависимости от числа дней после распускания почек. Найти скорость накопления сухой биомассы винограда в 10 дней от распускания почек».
Представим данные, собранные на факультете «Плодоовощеводство и виноградарство». На рисунке размещена сравнительная диаграмма успешности выполнения заданий контрольной работы в экспериментальной (ПВ1901) и контрольной (ПВ1902) группах.
Из рисунка видно, что результаты экспериментальной группы превышают результаты контрольной группы. Сравниваются средние показатели по группам только для задания 3, которое содержит понятие механического смысла производной, хорошо знакомое обучаемым еще со школы. Представленные профильные задачи охватывают те же элементы математических знаний, что и в номере 3, но сформулированная в них проблемная ситуация вызвала в контрольной группе серьезные затруднения.
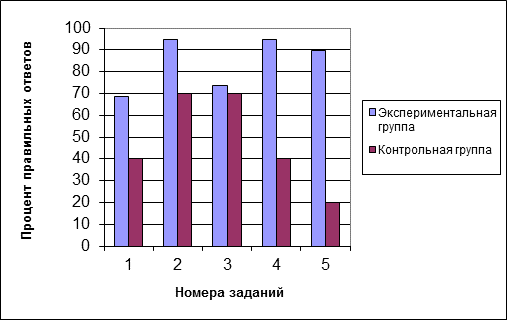
Сравнительная диаграмма успешности выполнения
контрольной работы по группам
В связи с этим выдвинем следующие статистические гипотезы.
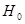: доля студентов, решивших от 4 до 5 задач, среди студентов экспериментальной группы не больше, чем среди студентов контрольной группы. 
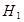: доля студентов, решивших от 4 до 5 задач контрольной работы, среди студентов экспериментальной группы больше, чем среди студентов контрольной группы.
Проверим это предположение с помощью углового преобразования Фишера для гипотез относительно доли успешности в этих группах, на уровне значимости 0,05. Число выполнивших более 4 заданий в экспериментальной группе составляет 16, в контрольной группе – 4, что составляет соответственно 80% (Р=0,8) и 20% (Р=0,2) от всех выполнивших эти задания. По формулам (1), (2) определим эмпирические значения критерия Фишера:
, 
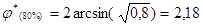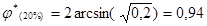. (1)
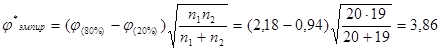. (2)
Из эталонной таблицы определяем критические значения для уровня значимости 0,05, принятого в педагогических исследованиях: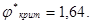 
При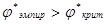 
гипотеза 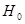отвергается и принимается гипотеза 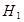. Таким образом, можно утверждать, что доля студентов экспериментальной группы, выполнивших 4 и более задания контрольной работы, выше соответствующей доли студентов контрольной группы. Отметим, что в экспериментальных и контрольных группах на других факультетах достигнуты аналогичные результаты.
Итоги выполнения контрольной работы показывают, что, несмотря на теоретическое разъяснение профильного смысла производной, студенты контрольной группы неуверенно решают профильные задачи, не умеют интерпретировать предложенную ситуацию из профильной дисциплины в математических понятиях и терминах, а также хуже освоили математическое содержание. В экспериментальной группе мы наблюдаем не только сформированность умения решать профильные задачи как следствие понимания профильного текста, но и повышение в целом математической подготовки по данной учебной теме. Это можно считать ожидаемым результатом работы студентов с герменевтическим структурированием в процессе решения профильной задачи.
Заключение. Представленные результаты подтверждают важность продолжения педагогических исследований в области реализации профессионально ориентированного обучения, включая разработку средств обучения на основе профильных задач. Выявлена необходимость дальнейшего изучения процесса понимания профильной задачи. Экспериментально подтверждена эффективность восприятия учебных математических текстов сложной структуры посредством использования при их решении герменевтического подхода.