Метод подсчета параметров широко применяется в физике, механике, математике и других областях науки и техники [1-3]. В геометрии параметризация используется прежде всего при решении задач исследовательского характера. При этом в существующей литературе очень мало примеров применения метода параметризации при решении геометрических задач [4]. Поэтому в данной статье предпринята попытка обоснования необходимости использования метода подсчета параметров при работе с геометрической задачей.
Цель статьи – систематизировать основные теоретические сведения о методе параметризации как дидактическом средстве анализа условия планиметрических задач, теоретически обосновать важность применения метода параметризации при анализе геометрической задачи и предложить методические рекомендации по его использованию.
Материал и методы исследования
Для разработки методических рекомендаций к работе над геометрической задачей были изучены теоретические вопросы обоснования принципов параметризации, проведен логико-математический анализ задачного материала, представленного в школьных учебниках и в учебниках для педагогических вузов. Также был осуществлен анализ методической литературы и публикаций, связанных с обоснованием принципов параметризации.
Результаты исследования и их обсуждение
С целью обоснования важности применения метода параметризации к анализу условия геометрической задачи и составления методических рекомендаций по его применению представляется необходимым рассмотрение основных теоретических положений указанного метода.
Поскольку в систематическом изложении основ параметрического метода, представленного в работах Н. Ф. Четверухина, Л. А. Яцкевича, Л. Н. Бескина, авторы используют разную терминологию и различные обозначения для числа параметров, то считаем возможным и целесообразным рассмотреть основные понятия и определения [5, 6].
Под параметрами в геометрии понимаются независимые величины, позволяющие выделить определенную геометрическую фигуру из множества фигур, соответствующего их определению [5, с. 15].
Если рассматривать фигуру 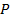 , «свободно плавающую в пространстве», то можно сказать, что при любом движении ее размеры и форма не меняются. Однако если в пространстве задать прямоугольную систему координат
, «свободно плавающую в пространстве», то можно сказать, что при любом движении ее размеры и форма не меняются. Однако если в пространстве задать прямоугольную систему координат 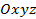 , то при движении фигуры
, то при движении фигуры 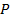 будут меняться координаты ее точек и ее положение относительно системы координат. Фигура
будут меняться координаты ее точек и ее положение относительно системы координат. Фигура 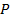 и равная ей фигура
и равная ей фигура 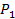 имеют одинаковые размеры и форму, но различаются своим положением в пространстве (рис. 1). Например, отрезки
имеют одинаковые размеры и форму, но различаются своим положением в пространстве (рис. 1). Например, отрезки 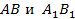 равны, но отрезки
равны, но отрезки 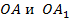 , зависящие от положения фигур в пространстве, не равны.
, зависящие от положения фигур в пространстве, не равны.
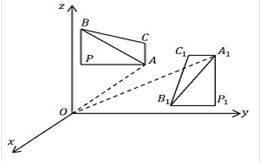
Рис. 1. Инварианты: соответствующие элементы равных фигур
Иными словами, равные фигуры имеют одинаковые размер и форму, но разное положение в пространстве. При изучении геометрических фигур чаще всего важны именно те величины, которые не меняются при движении. Обычно в геометрии такие величины называются инвариантами.
Инвариантом называется величина, определенная для данной фигуры и не меняющаяся при любых ее движениях [6, с. 27].
Предположим, что мы рассматриваем фигуру не произвольного вида, а какого-то определенного, принадлежащего к некоторому классу фигур: треугольник, окружность, параллелограмм, плоскость и т.д. Каждая из них имеет бесчисленное количество инвариантов (хотя бы отрезки, соединяющие любую пару точек), однако для однозначного определения фигуры достаточно знать лишь несколько инвариантов. Так, для задания треугольника достаточно знать длины его трех сторон, все остальные элементы треугольника при этом определяются однозначно. Вместо трех сторон для задания треугольника можно взять какие-то другие три элемента, например две стороны и угол между ними, сторону и два прилежащих к ней угла или две стороны и радиус описанной окружности. Но если мы знаем сторону треугольника 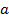 , противолежащий ей угол
, противолежащий ей угол 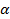 и радиус
и радиус 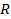 описанной около треугольника окружности, то построить однозначно такой треугольник мы не можем, так как таким набором инвариантов описывается бесконечно много не равных между собой треугольников.
описанной около треугольника окружности, то построить однозначно такой треугольник мы не можем, так как таким набором инвариантов описывается бесконечно много не равных между собой треугольников. Причина в том, что указанные величины не являются независимыми, они связаны соотношением:
Причина в том, что указанные величины не являются независимыми, они связаны соотношением: 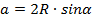 . Заметим, что такая задача при задании конкретных числовых значений этих величин либо является неопределенной (если эти величины удовлетворяют данному соотношению), либо не имеет решения, так как это соотношение не выполняется.
. Заметим, что такая задача при задании конкретных числовых значений этих величин либо является неопределенной (если эти величины удовлетворяют данному соотношению), либо не имеет решения, так как это соотношение не выполняется.
Поэтому, решая задачу об определении оптимального количества инвариантов для выделения одной фигуры из определенного класса одноименных неравных фигур, нужно быть уверенными в том, что через них могут быть выражены все остальные инварианты, присущие данной фигуре. Но при этом нужно следить и за независимостью выбранных инвариантов, чтобы они не были связаны каким-либо равенством, что приводит к возможности выразить какой-то из них через остальные.
Те независимые инварианты, которые определяют фигуру из данного класса с точностью до движения в пространстве, называются параметрами. Число параметров обозначается 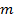 [6, с. 28].
[6, с. 28].
Н.Ф. Четверухин и Л.А. Яцкевич параметры, определяющие фигуру с точностью до движения, называют внутренними параметрами, а также ими доказано, что число внутренних параметров геометрической фигуры не зависит от выбора системы их подсчета [5, с. 18–19]. Можно сказать, что этим объясняется большое количество задач на построение треугольника или четырехугольника по разнообразным наборам определяющих элементов. В качестве примера можно рассмотреть в учебнике Л.С. Атанасяна и др. «Геометрия 7–9 кл.» следующие задачи:
1) постройте треугольник по двум сторонам и медиане, проведенной к третьей стороне;
2) постройте треугольник по стороне, высоте, проведенной к ней, и медиане, проведенной к одной из двух других сторон;
3) постройте треугольник по стороне, высоте и медиане, проведенным к этой стороне [7, с. 90–91].
Из определения понятия «внутренние параметры фигуры» следует, что, если задать необходимое и достаточное число параметров, придавая им конкретные числовые значения, то можно построить рассматриваемую фигуру либо конечное число фигур.
Укажем число внутренних параметров для некоторых фигур.
1. Точка, прямая и плоскость не имеют внутренних параметров, для любой из этих фигур 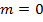 .
.
2. Отрезок характеризуется только длиной: два различных отрезка равны между собой тогда и только тогда, когда они имеют одинаковые длины. Таким образом, 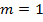 .
.
3. Треугольник. Из школьного курса геометрии известно, что в любом признаке равенства треугольников перечисляются три независимых элемента, отсюда можно сделать вывод, что для треугольника число внутренних параметров равно 3. Можно рассуждать и по-другому. Две вершины треугольника определяют сторону – отрезок, для которого 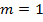 . Для построения третьей вершины достаточно знать еще два параметра, например расстояния от уже построенных двух вершин. Таким образом, для треугольника
. Для построения третьей вершины достаточно знать еще два параметра, например расстояния от уже построенных двух вершин. Таким образом, для треугольника 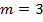 .
.
4. Плоский многоугольник с 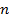 вершинами
вершинами 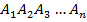 . Три вершины определяются тремя параметрами. Для построения каждой следующей из
. Три вершины определяются тремя параметрами. Для построения каждой следующей из 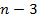 оставшихся вершин необходимо и достаточно затратить 2 параметра, например расстояния от уже построенных двух вершин. Следовательно,
оставшихся вершин необходимо и достаточно затратить 2 параметра, например расстояния от уже построенных двух вершин. Следовательно, 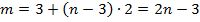 .
.
5. Окружность. Две окружности с равными радиусами равны, следовательно, 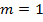 .
.
6. Пара параллельных прямых определяется одним параметром – расстоянием между ними,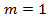 .
.
7. Пара пересекающихся прямых также определяется одним параметром – величиной угла, 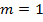 .
.
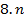 -угольная пирамида
-угольная пирамида 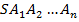 . В основании n-угольной пирамиды лежит плоский -угольник, который определяется
. В основании n-угольной пирамиды лежит плоский -угольник, который определяется 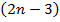 -мя параметрами. Для определения вершины
-мя параметрами. Для определения вершины 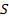 пирамиды требуется затратить еще 3 параметра, например расстояния
пирамиды требуется затратить еще 3 параметра, например расстояния 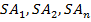 до трех вершин основания. (Можно также взять расстояние
до трех вершин основания. (Можно также взять расстояние 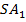 до вершины
до вершины 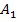 основания и углы
основания и углы 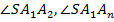 , образованные этим боковым ребром со сторонами
, образованные этим боковым ребром со сторонами 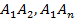 . Вместо вершины
. Вместо вершины 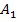 можно взять любую вершину основания.) Таким образом, n-угольная пирамида определяется
можно взять любую вершину основания.) Таким образом, n-угольная пирамида определяется 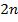 параметрами.
параметрами.
9. Тетраэдр. Тетраэдром называют многогранник, поверхность которого ограничена четырьмя треугольниками. Главная отличительная особенность тетраэдра – все его грани равноправны между собой. Число параметров, определяющих тетраэдр, можно определить как для треугольной пирамиды: 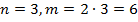 .
.
Параметры, определяющие фигуру, могут иметь размерность (длину, площадь, объем) либо быть безразмерными (угол, отношение длин отрезков). При этом один из 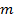 параметров, определяющих фигуру, должен иметь размерность. Остальные
параметров, определяющих фигуру, должен иметь размерность. Остальные 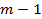 параметров могут быть безразмерными. Если в задаче даны только безразмерные параметры, то фигура не может быть определена однозначно с точностью до движения, ее можно определить только с точностью до подобия.
параметров могут быть безразмерными. Если в задаче даны только безразмерные параметры, то фигура не может быть определена однозначно с точностью до движения, ее можно определить только с точностью до подобия.
Часто в задачах вместо значений параметров указывается некоторая информация о фигуре. Поэтому важно определить, сколько параметров нам заменяет та или иная информация о ней. Так, например, чтобы задать четырехугольник, необходимо и достаточно знать пять параметров. Определим «параметрическую цену» информации о четырехугольниках, которая заключена в их определениях.
Трапеция по определению имеет одну пару параллельных сторон, следовательно, термин «трапеция» заменяет 1 безразмерный параметр. Таким образом, для задания трапеции необходимы только 4 параметра.
Прямоугольная трапеция – дополнительно известно, что одна из боковых сторон составляет с основаниями прямые углы, т.е. добавляется еще один безразмерный параметр. Термин «прямоугольная трапеция» заменяет 2 безразмерных параметра. Следовательно, для задания прямоугольной трапеции необходимы только 3 параметра.
Аналогично термин «равнобедренная трапеция» заменяет 2 безразмерных параметра (отношение боковых сторон равно 1). Для определения равнобедренной трапеции нужно задать всего 3 параметра.
Параллелограмм по определению имеет две пары параллельных сторон, т.е. термин «параллелограмм» заменяет 2 безразмерных параметра. Для определения параллелограмма необходимо и достаточно знать 3 параметра.
Аналогичными рассуждениями можно определить «параметрическую цену» следующих терминов: «прямоугольник» – три параметра, «ромб» – три параметра, «правильный четырехугольник» (т.е. «квадрат») – четыре параметра, «вписанный четырехугольник» – один параметр, «описанный четырехугольник» – один параметр.
Заметим, что информация, заключенная в терминах, дает нам только безразмерные параметры.
Число параметров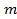 , которыми обладает фигура данного класса, характеризует изменчивость или гибкость ее формы: чем больше число
, которыми обладает фигура данного класса, характеризует изменчивость или гибкость ее формы: чем больше число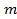 , тем более разнообразные фигуры могут получиться при изменении параметров какой-то одной из них. Например, произвольные треугольники (три параметра) более разнообразны, чем равнобедренные (два параметра), а эти более разнообразны, чем равносторонние (один параметр), которые все подобны друг другу. Наконец, все равносторонние треугольники со стороной 1 см (нуль параметров) просто все равны и могут лишь занимать разные положения в пространстве.
, тем более разнообразные фигуры могут получиться при изменении параметров какой-то одной из них. Например, произвольные треугольники (три параметра) более разнообразны, чем равнобедренные (два параметра), а эти более разнообразны, чем равносторонние (один параметр), которые все подобны друг другу. Наконец, все равносторонние треугольники со стороной 1 см (нуль параметров) просто все равны и могут лишь занимать разные положения в пространстве.
Каждый параметр может изменяться непрерывно, принимая любые действительные значения в некоторых пределах. Поэтому, если число параметров 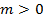 , то данный класс уже содержит бесконечное множество фигур. Чтобы подчеркнуть, «как много» фигур содержит класс фигур, соответствующих данному определению, употребляют такой оборот речи: «класс фигур с
, то данный класс уже содержит бесконечное множество фигур. Чтобы подчеркнуть, «как много» фигур содержит класс фигур, соответствующих данному определению, употребляют такой оборот речи: «класс фигур с 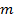 параметрами содержит
параметрами содержит 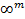 фигур». Например, множество всех не равных между собой треугольников содержит
фигур». Например, множество всех не равных между собой треугольников содержит 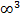 фигур, можно сказать также: «Все треугольники составляют трехпараметрическое множество». Все окружности составляют однопараметрическое множество, поэтому всех треугольников «больше», чем всех окружностей.
фигур, можно сказать также: «Все треугольники составляют трехпараметрическое множество». Все окружности составляют однопараметрическое множество, поэтому всех треугольников «больше», чем всех окружностей.
Таким образом, внутренние параметры позволяют нам указать определенную фигуру из целого класса фигур, соответствующих данному определению. При этом:
1) равные фигуры в данном классе фигур имеют одинаковые значения внутренних параметров;
2) неравные фигуры имеют неодинаковые значения хотя бы одного параметра.
Иногда в условии геометрической задачи имеется требование определенного расположения искомой фигуры относительно данных фигур. В таком случае имеют значение не только определяющие ее инварианты, но и положение этой фигуры, поскольку в этой ситуации равные друг другу, но различные фигуры по-разному расположены в пространстве, следовательно, не могут считаться за одну. В таких задачах нужно учитывать и число внутренних, и число внешних параметров фигуры.
В качестве примера рассмотрим следующие задачи [7, c. 51].
Постройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой.
Постройте окружность данного радиуса, проходящую через две данные точки.
Операция подсчета числа параметров, необходимых для выделения определенного положения фигуры из данного множества всех конгруэнтных фигур в пространстве, называется внешней параметризацией [5, с. 15]. Число параметров внешней параметризации обозначается 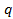 .
.
Для определения числа 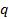 внешних параметров различных фигур подразумевается, что задана прямоугольная декартова система координат в пространстве либо на плоскости. При этом положение фигуры определяется координатами ее точек в соответствующей системе координат.
внешних параметров различных фигур подразумевается, что задана прямоугольная декартова система координат в пространстве либо на плоскости. При этом положение фигуры определяется координатами ее точек в соответствующей системе координат.
Число внешних параметров фигуры в геометрии выражает то же самое, что и число степеней свободы в механике [5, с. 15]. Из механики известно, что число степеней свободы твердого тела на плоскости равно 3, а в пространстве равно 6. Это подтверждается также и такими соображениями: формулы движения плоскости зависят от трех параметров, а формулы движения пространства – от 6 параметров.
Независимые числа, определяющие фигуру из данного класса, включая ее положение в пространстве, называются параметрами положения. Число параметров положения будем обозначать 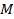 [6, с. 31].
[6, с. 31].
Число параметров положения характеризует разнообразие фигур, принадлежащих какому-либо классу. При изменении значений внутренних параметров будут меняться размеры или форма данной фигуры, при изменении положения фигуры в пространстве будут получаться фигуры, равные данной.
Заметим, что, подсчитывая число параметров положения фигуры, мы уже не можем представлять ее «свободно плавающей в пространстве». Обязательно должна быть определена (или, по крайней мере, подразумеваться) система координат.
Рассмотрим несколько примеров подсчета параметров положения и внешних параметров геометрических фигур.
1. Точка.
1) точка на прямой определяется своей координатой в выбранной системе координат на этой прямой. Следовательно, 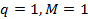 ;
;
2) точка на плоскости определяется своими координатами в выбранной системе координат на плоскости, следовательно, 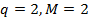 ;
;
3) положение точки в пространстве определяется тремя координатами: 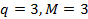 .
.
2. Прямая.
Прямая, как и точка, не имеет внутренних параметров. Обычно прямая задается двумя точками. При таком способе задания определяются и «лишние» элементы, а именно длина отрезка между этими точками и положение этого отрезка на прямой. Поэтому при подсчете числа параметров положения приходится вычитать эти два «лишних» параметра.
1) прямая на плоскости. Две точки определяются четырьмя параметрами, следовательно, 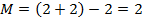 ;
;
2) прямая в пространстве. Две точки определяются шестью параметрами, следовательно, 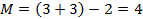 .
.
3. Плоскость может быть определена тремя точками, не лежащими на одной прямой. При таком способе задания также определены «лишние» элементы: треугольник с вершинами в этих точках (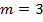 ) и положение этого треугольника на плоскости
) и положение этого треугольника на плоскости 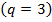 . Поэтому плоскость в пространстве определяется тремя параметрами:
. Поэтому плоскость в пространстве определяется тремя параметрами: 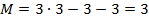 .
.
Параметрический метод дает возможность, проанализировав условие задачи, выяснить, является ли данная задача определенной, неопределенной или переопределенной. В первом случае задача имеет конечное число решений, которые, в принципе, все можно отыскать. Во втором случае задача имеет бесконечно много различных решений, которые можно будет при необходимости как-то классифицировать. Если же задача переопределена, то какие-то данные в условии либо излишни, так как определяются через другие, либо противоречат остальным, и, следовательно, задача не имеет решений.
В данной статье нас интересует применение внутренней параметризации при анализе условия геометрических задач. Рассмотрим несколько примеров.
1. В выпуклом четырехугольнике 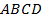 известны стороны и диагональ:
известны стороны и диагональ: 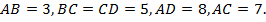
а) докажите, что вокруг этого четырехугольника можно описать окружность;
б) найдите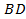 .
.
Оценим параметрическую определенность четырехугольника 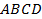 . Плоский четырехугольник определяется пятью параметрами. В данном случае даны четыре стороны и диагональ, поэтому четырехугольник
. Плоский четырехугольник определяется пятью параметрами. В данном случае даны четыре стороны и диагональ, поэтому четырехугольник 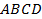 полностью определен. Это значит, что, выбрав единичный отрезок, мы можем его построить. Следовательно, все его элементы могут быть определены, в том числе и углы. Выпуклый четырехугольник является вписанным в окружность тогда и только тогда, когда сумма двух его противоположных углов равна
полностью определен. Это значит, что, выбрав единичный отрезок, мы можем его построить. Следовательно, все его элементы могут быть определены, в том числе и углы. Выпуклый четырехугольник является вписанным в окружность тогда и только тогда, когда сумма двух его противоположных углов равна 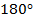 . Как известно, косинусы углов, сумма которых равна
. Как известно, косинусы углов, сумма которых равна 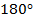 , являются противоположными числами. Поэтому, вычислив по теореме косинусов косинус угла
, являются противоположными числами. Поэтому, вычислив по теореме косинусов косинус угла  в треугольнике
в треугольнике  и косинус угла
и косинус угла 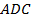 в треугольнике
в треугольнике 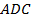 , мы можем выполнить задание а).
, мы можем выполнить задание а).
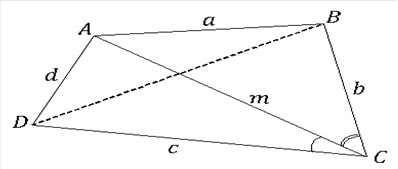
Рис. 2. Параметрическая определенность четырехугольника
Теперь ясно, что для ответа на второй вопрос нужно рассмотреть два других треугольника и, учитывая, что 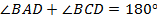 , найти
, найти 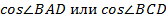 , а затем найти
, а затем найти 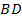 .
.
Заметим, что в этой задаче длины сторон подобраны так, что четырехугольник 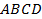 вписан в окружность. Однако все остальные элементы четырехугольника можно определить и в общем случае. Например, для вычисления длины диагонали
вписан в окружность. Однако все остальные элементы четырехугольника можно определить и в общем случае. Например, для вычисления длины диагонали 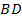 можно действовать по следующему плану: 1) найти косинус и синус угла
можно действовать по следующему плану: 1) найти косинус и синус угла 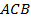 ; 2) найти косинус и синус угла
; 2) найти косинус и синус угла 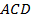 ; 3) вычислить косинус угла
; 3) вычислить косинус угла 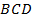 по формуле косинуса суммы двух углов; 4) вычислить
по формуле косинуса суммы двух углов; 4) вычислить 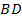 по теореме косинусов (рис. 2).
по теореме косинусов (рис. 2).
На сторонах 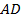 и
и 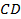 ромба
ромба 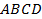 отмечены точки
отмечены точки 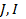 и
и 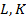 соответственно, причем так, что
соответственно, причем так, что 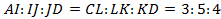 (рис. 3).
(рис. 3).
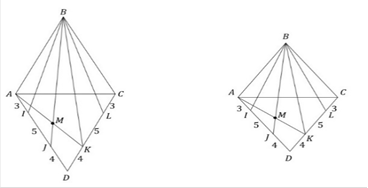
Рис. 3. Параметическая неопределенность ромба
а) Докажите, что прямые 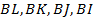 делят меньшую диагональ
делят меньшую диагональ 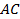 на 5 равных отрезков.
на 5 равных отрезков.
б) Найдите площадь треугольника 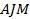 , где
, где 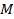 – точка пересечения прямых
– точка пересечения прямых 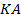 и
и 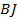 , если известно, что площадь ромба равна 72.
, если известно, что площадь ромба равна 72.
Информация «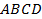 – ромб» определяет два параметра, величина площади – еще один. Недостаточно параметров, чтобы определить ромб даже с точностью до подобия. Поэтому условие задачи определяет «просто ромб», но нам неизвестны ни длина его стороны, ни величина угла. Задача может быть решена, но никакие линейные величины ромба не могут быть определены. Таким образом, в пункте а) доказывается свойство, присущее всем ромбам.
– ромб» определяет два параметра, величина площади – еще один. Недостаточно параметров, чтобы определить ромб даже с точностью до подобия. Поэтому условие задачи определяет «просто ромб», но нам неизвестны ни длина его стороны, ни величина угла. Задача может быть решена, но никакие линейные величины ромба не могут быть определены. Таким образом, в пункте а) доказывается свойство, присущее всем ромбам.
2. В треугольнике 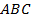 проведена биссектриса
проведена биссектриса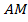 . Прямая, проходящая через вершину
. Прямая, проходящая через вершину  перпендикулярно
перпендикулярно  , пересекает сторону
, пересекает сторону  в точке
в точке  .
. 
а) Докажите, что биссектриса угла 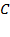 делит отрезок
делит отрезок 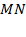 пополам.
пополам.
б) Пусть 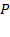 – точка пересечения биссектрис треугольника
– точка пересечения биссектрис треугольника 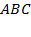 . Найдите отношение
. Найдите отношение 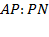 .
.
Оценим параметрическую определенность треугольника 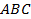 . Плоский треугольник определяется тремя параметрами. В данном случае даны три стороны, поэтому треугольник
. Плоский треугольник определяется тремя параметрами. В данном случае даны три стороны, поэтому треугольник 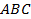 полностью определен. Это значит, что, выбрав единичный отрезок, мы можем его построить. Следовательно, все его элементы могут быть определены, в том числе и отрезки.
полностью определен. Это значит, что, выбрав единичный отрезок, мы можем его построить. Следовательно, все его элементы могут быть определены, в том числе и отрезки.
Чтобы доказать, что биссектриса угла 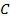 делит отрезок
делит отрезок 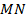 пополам, достаточно убедиться в том, что треугольник
пополам, достаточно убедиться в том, что треугольник 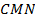 – равнобедренный.
– равнобедренный.
Для ответа на второй вопрос можно воспользоваться свойством биссектрисы угла треугольника.
3. На диагонали параллелограмма взяли точку, отличную от ее середины. Из нее на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.
а) Докажите, что четырехугольник, образованный основаниями этих перпендикуляров, является трапецией.
б) Найдите площадь полученной трапеции, если площадь параллелограмма равна 16, а один из его углов равен 60°.
Информация «параллелограмм» определяет два параметра, величина площади и одного из углов – еще два. Недостаточно параметров, чтобы определить параллелограмм даже с точностью до подобия. Поэтому условие задачи определяет «просто параллелограмм», следовательно, в пункте а) доказывается свойство, присущее всем параллелограммам. Задача может быть решена, но никакие величины параллелограмма не могут быть определены.
4. Дан выпуклый четырехугольник 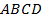 . Докажите, что отрезки
. Докажите, что отрезки 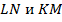 , соединяющие середины его противоположных сторон, делят друг друга пополам.
, соединяющие середины его противоположных сторон, делят друг друга пополам.
В данной задаче нам не дан ни один параметр. Поэтому мы не можем выделить этот четырехугольник из класса всех четырехугольников. Доказанное свойство будет справедливо для любого четырехугольника.
При решении геометрической задачи представляется важным понимать, какому именно множеству принадлежит фигура, в чем сходство и различие фигур, которые описываются условиями данной задачи. В учебниках геометрии для классов с углубленным изучением математики встречаются задачи исследовательского характера. Это, например задачи, в которых ставятся вопросы типа: «Как найти ту или иную величину, если известны несколько величин, определяющих данную фигуру», «Как изготовить модель той или иной фигуры» [8, 9, 10].
В качестве примера рассмотрим задачу, приведенную в учебнике А.Д. Александрова и др. «Геометрия 8–9» [10].
Как сделать трапецию, у которой: а) три стороны равны, а диагональ имеет данную длину; б) две стороны равны, а диагонали перпендикулярны; в) три стороны равны, а диагональ равна большей стороне; г) боковые стороны равны, диагонали перпендикулярны, угол при основании равен 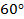 , а площадь равна 1; д) боковая сторона перпендикулярна основанию, диагональ является биссектрисой, а площадь равна 1; е) три стороны равны, угол между диагоналями равен
, а площадь равна 1; д) боковая сторона перпендикулярна основанию, диагональ является биссектрисой, а площадь равна 1; е) три стороны равны, угол между диагоналями равен 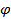 , а площадь равна 1 [10, с. 145]?
, а площадь равна 1 [10, с. 145]?
Рекомендации. При решении предложенной задачи учащиеся сами должны оценить, все ли данные величины нужны для решения задачи, можно ли определить однозначно фигуру, задаваемую условием задачи, либо решить, какие именно величины и в каком количестве необходимы.
а) Если у трапеции равны три стороны, то это могут быть две боковые стороны и одно из оснований. Следовательно, нужно построить равнобедренную трапецию, одно из оснований которой равно боковой стороне. Термин «равнобедренная трапеция» определяет два параметра, условие «одно из оснований равно боковой стороне» – один параметр. Эти три параметра – безразмерные. Длина диагонали – еще один, но уже размерный параметр. Таким образом, нам известны четыре параметра, но для определения четырехугольника необходимы 5 параметров. Следовательно, задача неопределенная, данные условия описывают однопараметрическое семейство трапеций. Для построения какой-либо трапеции, удовлетворяющей этим условиям, мы можем дополнительно задать, например, длину боковой стороны. При этом нужно учитывать, что длина диагонали должна быть меньше удвоенной боковой стороны (для построения треугольника по трем сторонам нужно, чтобы их длины удовлетворяли неравенству треугольника).
б) Три стороны равны, а диагональ равна большей стороне.
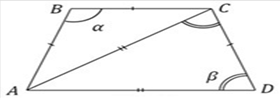
Рис. 4. Безразмерные параметры, определяющие трапецию с точностью до подобия
Как и в предыдущем случае, условие «у трапеции равны три стороны» определяет три безразмерных параметра. Предположим, что при этом диагональ равна боковой стороне. Тогда основание, диагональ и боковая сторона должны образовывать правильный треугольник, следовательно, в этом случае диагональ и боковая сторона образуют с основанием равные углы, что невозможно в равнобедренной трапеции. Значит, в условии задачи описывается равнобедренная трапеция, у которой меньшее основание равно боковой стороне, а большее основание равно диагонали. Итого израсходовано четыре параметра. Заметим, что условие задачи позволяет вычислить углы этой трапеции и зависимость между длинами оснований.
Пусть в трапеции 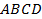 :
: 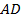 и
и 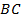 – основания,
– основания, 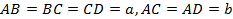 . Тогда треугольники
. Тогда треугольники 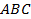 и
и 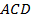 равнобедренные. Обозначив
равнобедренные. Обозначив 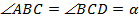 ,
, 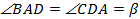 (рис. 4), получим систему двух уравнений:
(рис. 4), получим систему двух уравнений: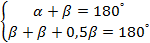 . Следовательно,
. Следовательно, 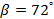 ,
, 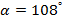 . Таким образом, условия задачи описывают однопараметрическое семейство подобных трапеций, основания которой связаны зависимостью:
. Таким образом, условия задачи описывают однопараметрическое семейство подобных трапеций, основания которой связаны зависимостью: 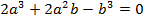 .
.
Выводы
Считаем, что представленные в статье основные теоретические сведения о методе параметризации как средстве анализа условия геометрических задач и методические рекомендации по его применению предоставят возможность каждому студенту или школьнику, интересующемуся математикой, решать задачи исследовательского характера. Также метод параметризации позволит самим составлять задачи, оценивая их условия с точки зрения возможности решения, что будет являться одним из факторов успешного решения геометрических задач.



