Производящей функцией для числовой последовательности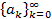 
, называется символ вида 
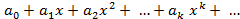, то есть формальный ряд, обычно обозначаемый одной буквой, например 
:
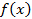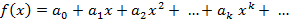(1)
Пример 1. Для постоянной последовательности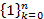 
будем иметь
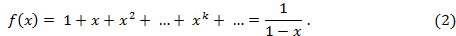
Здесь формальный ряд оказался сходящимся в области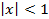 
к сумме 
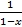. Заметим, однако, что в теории производящих функций вопросами сходимости рядов, как правило, не задаются. По этой причине их и называют формальными. Если же ряд оказывается сходящимся к сумме 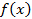, как это было в примере 1, то говорят, что 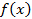есть замкнутая форма производящей функции. Понятие производящей функции вводится и для конечной последовательности чисел 
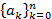. В этом случае говорят о производящем многочлене 
.
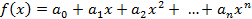Далее предполагается, что читатель знаком с начальными понятиями комбинаторики. В частности, с понятиями сочетания и сочетания с повторениями. А также формулами для подсчета их числа: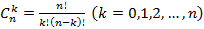 
и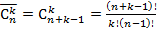 
.
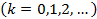Обратим внимание, что в отличие от чисел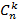 
числа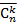 
определяются для 
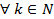. Таким образом, можно определить числовую последовательность 
.
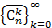Пример 2. Рассмотрим конечную последовательность чисел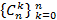 
и составим для неё производящую функцию (производящий многочлен)
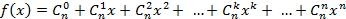. (3)
Как хорошо известно, многочлен (3) представляет собой формулу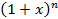 
, называемую формулой бинома Ньютона:
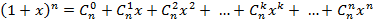. (4)
Коэффициент 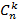равен количеству различных способов взятия 
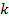букв 
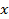из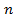
скобок
.
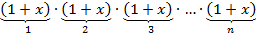Для числовой последовательности 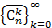также определим производящую функцию
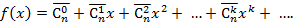
Имеет место следующая теорема.
Теорема 1. Для любого натурального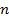 
справедлива формула
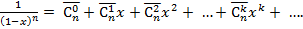(5)
Заметим, что доказательство формулы (5) в комбинаторном анализе проводится, как правило, методом математической индукции. Здесь же обратим внимание на следующее обстоятельство. Еще во времена Ньютона было известно разложение (оно изучается студентами первого курса втузов)
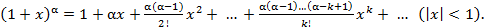(6)
Ряд справа в формуле (6) называется биномиальным. Ясно, что если рассмотреть частный случай (6), полагая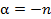 
и заменяя
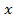на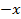 
, то получим в точности формулу (5), если же взять 
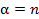, то получим формулу (4). Таким образом, теория рядов, имеющая многочисленные приложения в математическом анализе, нашла неожиданным образом приложения в разделе дискретной математики – комбинаторном анализе. Подобные следствия всегда способствуют повышению интереса к предмету обучения.
Выскажем теперь общий принцип решения задач комбинаторики с применением производящих функций [1]. При решении задач на подсчет числа сочетаний на первом шаге, исходя из анализа условий задачи, строится функция 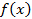, моделирующая процесс формирования сочетаний. Принцип построения 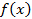берет начало от формулы бинома Ньютона, по этой причине мы уделили ей выше внимание. На втором шаге 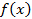разлагается по степеням 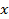(это разложение, по существу, есть первое представление производящей функции). В результате чего определяются комбинаторные числа, как коэффициенты при степенях 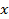. Учитывая, что алгоритм решения таких задач логически прост и понятен, дальнейшее изложение будет вестись преимущественно на языке примеров с конкретными оговорками учебно-методического характера и иметь демонстрационный характер.
Целью статьи является построение методики обучения решению задач комбинаторного анализа с применением производящих функций, а также обмен опытом преподавания этой темы во втузе.
Задачи перечислительной комбинаторики
Пусть имеется 5 шаров разных цветов: белый, синий, красный, желтый и зеленый. Обозначим это множество буквой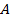 
, а шары соответственно буквами 
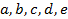. Таким образом 
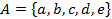(напомним, что при определении множества считается, что все его элементы различимы между собой). Далее из шаров множества мы будем конструировать сочетания, но при этом допускать, что некоторые шары в конкретных сочетаниях могут повторяться. Такие сочетания называются, как мы уже знаем, сочетаниями с повторениями. Введем в рассмотрение вектор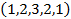 
. Будем его называть вектором спецификаций. Смысл компонент этого вектора следующий. В любое сочетание шары белого и зеленого цвета могут войти, но не более одного раза, шары синего и желтого цветов могут также повториться, но не более двух раз и, наконец, шар красного цвета может быть повторен, но не более 3 раз. Сформулируем теперь задачу.
Задача 1. Составить производящую функцию для определения числа сочетаний из данного набора шаров с повторениями, с учетом вектора спецификаций.
Так как различимых объектов пять, то функция 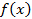, моделирующая процесс выбора, будет представлять собой произведение пяти сомножителей
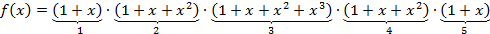(7)
Причем первый и пятый сомножители отвечают за выбор (или не выбор) белого и зеленого шаров; второй и четвертый сомножители – за выбор синих и желтых шаров, третий – за выбор красных шаров. Отметим, что если бы вектор спецификаций имел вид 
, то в скобках 2, 3 и 4 слагаемые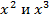 
отсутствовали и мы находились бы в условиях применения формулы бинома Ньютона. Таким образом, конструкция (7) обобщает формулу бинома Ньютона для 
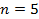. После раскрытия скобок в формуле (7) получим 144 слагаемых, каждое из которых отвечает определенной выборке (сочетанию). Например, если взять единицу из первой скобки, 
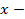из второй, 
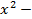из третьей, 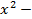из четвёртой и 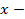из пятой, то получим 
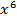. Эта степень отвечает конкретному сочетанию 
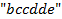. Единица же, взятая из первой скобки, говорит о том, что в данной выборке белого шара нет. Аналогично обстоит дело и с другими слагаемыми. Приводя подобные в указанной сумме, получим окончательный (говорят «распакованный») вид производящей функции
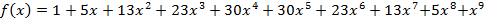. (8)
Коэффициенты в (8) при различных степенях 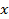определяют комбинаторные числа: числа сочетаний с повторениями с учетом введенной спецификации. Так, например, коэффициент при 
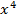равен 30. Он равен числу сочетаний с повторениями из 5 по 4. Перечислим эти сочетания: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
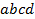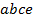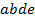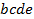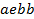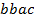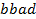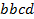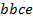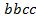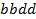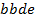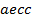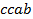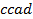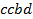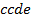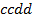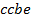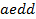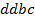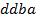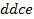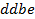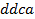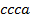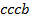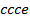. Остальные коэффициенты в формуле (8) позволяют ответить и на другие вопросы в рамках данной задачи. Заметим, что первый член в формуле (8) единица: ей отвечает пустое множество
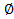, т. е. такое «сочетание», в котором элементов нет, коэффициент при 
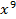также равен единице, так как из 5 шаров с учетом их максимального повторения можно составить только сочетание 
.
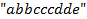Выше при составлении сочетаний мы использовали тот факт, что некоторые шары можно повторять. Конечно, можно было бы считать, что есть два синих, два желтых, три красных и по одному белому и зеленому шару (это отступление от традиционного определения понятия множества часто применяется). Используя эту трактовку, далее будем считать, что количество шаров всех цветов неограниченно. В этом случае будем говорить, что вектор спецификаций имеет вид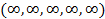 
. Тогда производящей функцией для определения всевозможных сочетаний будет
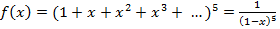. (9)
.
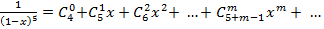Отсюда, например, находим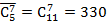 
. Ровно столько различных сочетаний по 7 шаров можно составить из 5, повторяя их цвет в конкретных выборках.
Задача 2. Требуется: 1. Составить производящую функцию 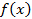для подсчета числа сочетаний различных по составу букетов из гвоздик трех цветов, причем в каждом букете должно быть белых и красных – четное число, а розовых – нечетное.
2. Найти число всевозможных по составу букетов из 15 гвоздик:
1) учитывая, что различимых объектов три, то в производящей функции 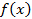будет три сомножителя;
2) в первых двух сомножителях, отвечающих белым и красным гвоздикам, будут присутствовать только четные степени ;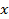
3) в третьем сомножителе, отвечающем розовым гвоздикам, – нечетные степени;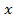
4) таким образом, производящая функция будет иметь вид
.
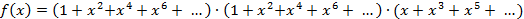5) для ответа на второй вопрос задачи представим 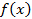следующим образом
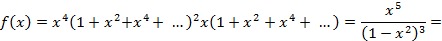
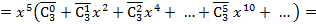
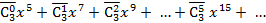
Ответ находится как коэффициент при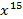 
: 
.
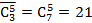Задача 3. Рассмотрим классическую задачу графа де Мере – о подбрасывании трёх игральных костей. Наблюдается величина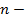 
сумма выпавших очков. Так как костей три, то производящая функция 
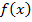для определения числа вариантов, дающих сумму в 
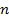очков, имеет структуру произведения трех одинаковых сомножителей
.
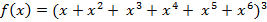Преобразуем её следующим образом
=
.
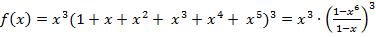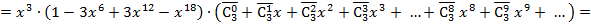
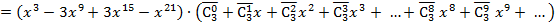Отсюда, например, можно найти число 27 – количество вариантов (сочетаний), дающих сумму в 11 очков, а также число 25 – количество вариантов, дающих сумму в 12 очков.
Замечание 2. Нет сомнений, что первоначально числа 27 и 25 были найдены непосредственным подсчетом соответствующих комбинаций. В курсе теории вероятностей студенты также перебором находили эти числа. Примененный нами метод обладает общностью. Легко видеть, что количество игральных костей три не принципиально и может быть взято любым, и простой перебор искомых вариантов становится необозримым.
Задача 4. Пусть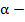 
натуральное шестизначное число из промежутка 
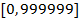. Каждое число будем записывать в виде 
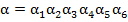. Число 
будем называть счастливым, если сумма цифр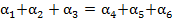 
. Зададимся вопросом: «Сколько среди миллиона чисел счастливых?»
Эта задача сложнее предыдущих, и существует несколько вариантов ее решения, но мы остановимся на одном. Для этого рассмотрим отображение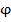 
, ставящее каждому 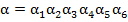число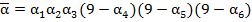 
. Справедлива
Теорема 2. Если число 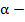счастливое, то сумма цифр числа 
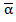равна 27. И наоборот, если для числа сумма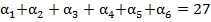 
, то число 
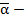счастливое.
Доказательство. Пусть выполняется равенство 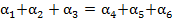, т.е. число 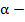счастливое. Тогда 
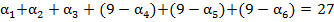. Что означает, что сумма цифр шестизначного числа 
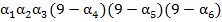равна 27. С другой стороны, пусть 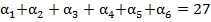. Отсюда вытекает, что 
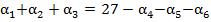. Или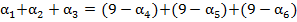 
. Следовательно, число 
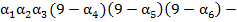счастливое.
Примеры.
1. Очевидно, что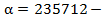 
счастливое число. Найдем по указанному правилу его образ 
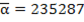. Видно, что 
.
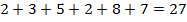2. Возьмём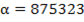 
. Для него сумма 
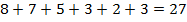. Найдем его образ 
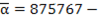это счастливое число.
Как следствие из теоремы 1 вытекает необходимая нам теорема.
Теорема 3. Количество всех счастливых чисел равно количеству чисел, сумма цифр которых равна 27.
Таким образом, чтобы ответить на поставленный вопрос, необходимо подсчитать количество чисел , для которых
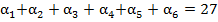. (9)
Замечание 3. Важно, что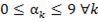 
, так как здесь идет речь не о количестве решений уравнения (9) в области 
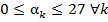, которое определяется числом 
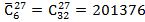, а в более узкой области .
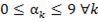Для решения уравнения (9) составим производящую функцию
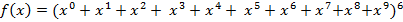
и представим ее в виде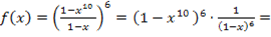 
.
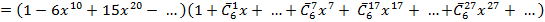Отсюда легко находится коэффициент при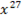 
:
.
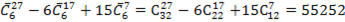Замечание 4. Рассмотренная задача имеет большую историю. Люди старшего поколения хорошо помнят, как выглядели билеты в автобусах, троллейбусах и трамваях. На них были номера из 6 цифр. В то время существовали и определенные приметы о значении этих цифр. Студенты, например, полагали, что если сумма первых цифр совпадала с суммой трех последних, то может повезти, например на экзамене, и такие билеты называли счастливыми, а иногда и съедали. Естественно, находились и такие студенты, которые задавались вопросом, насколько часто может встретиться счастливый билет. Из решения этой задачи следует, что вероятность, что счастливый билет улыбнется студенту, достаточно большая и примерно равна 0,055, или один из 18 билетов будет таким. Второй широко известный метод решения этой задачи основан на принципе включения-исключения. С ним можно познакомиться по книгам [2-4].
Заключение. Метод производящих функций – один из самых эффективных и развитых методов решения задач комбинаторного анализа. Идеи метода были заложены еще Лапласом в XVIII веке и связаны с решением некоторых вероятностных задач. В статье мы спроектировали канву одного, возможно, двух практических занятий на его использование при решении простейших задач. Важно, что принцип построения производящих функций восходит к биному Ньютона и логически связан с ним. На этом надо четко акцентировать внимание обучаемых. Методическая ценность изложенного вопроса заключается также в том, что формируемые в процессе решения задач знания интегрируют и систематизируют две математические дисциплины: теорию рядов и комбинаторику. Тем самым достигается некоторая комплексность формируемых знаний.
Учитывая, что современные рабочие программы по математике в технических вузах достаточно насыщены материалом, не исключено, что изложенные выше вопросы не найдут места в тематических планах. Тогда их можно частично вынести на самостоятельную работу, организовав при этом форму отчетности. Кроме того, думается, что рассмотренный нами материал доступен не только студентам технических вузов, а это, как правило, первокурсники, но и школьникам физико-математических классов, после некоторой его адаптации [5].