Сахарный диабет (СД) представляет собой глобальную медико-социальную проблему, значимость которой неуклонно возрастает [1]. Основополагающий принцип лечения СД и профилактики его осложнений – поддержание адекватного гликемического контроля, одной из важных характеристик которого является обеспечение невысокой вариабельности глюкозы крови [2].
В последнее время накапливается все больше данных о влиянии вариабельности гликемии (ВГ) на развитие диабетических осложнений [3, 4], однако вопрос о стандартизации методов ее оценки остается открытым [5]. На настоящий момент предложено большое количество показателей ВГ [3, 6], одним из которых является средняя амплитуда гликемических экскурсий.
Средняя амплитуда гликемических экскурсий (Mean amplitude of glycemic excursions, MAGE) – параметр ВГ, представляющий собой среднее арифметическое амплитуд колебаний гликемии, превышающих величину 1 стандартного отклонения (Standart Deviation, SD).
Впервые параметр MAGE был предложен F.J. Service и соавт. [7]. В этой же работе подробно описан графический способ расчета этого показателя, признающийся большинством исследователей «золотым стандартом» [8, 9, 10]. В последующем было разработано несколько формул для расчета MAGE, среди которых в литературе наиболее часто используется следующая:
MAGE = 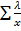 , если λ > 1 v,
, если λ > 1 v,
где λ – амплитуда отдельного колебания гликемии, х – количество колебаний, v – стандартное отклонение от среднего уровня гликемии за 24-часовой период [6]. При расчете MAGE оригинальным способом наиболее трудоемким этапом является определение значения λ с учетом целого ряда критериев [7], что приводит к большим временным затратам при вычислении и оператор-зависимости метода [10]. В связи с этим актуальной проблемой является создание компьютерных алгоритмов вычисления MAGE. В настоящее время создано несколько программ для расчета этого параметра, основанных на методе непрерывного мониторинга глюкозы (НМГ) и имеющих хорошую сопоставимость с оригинальным графическим способом расчета [8, 9].
Самостоятельный мониторинг глюкозы крови (СМГК) – альтернатива НМГ при первичном сборе информации о вариабельности гликемии. В основе СМГК лежит анализ данных самоконтроля пациентов, полученных с помощью индивидуальных глюкометров, что обусловливает доступность и невысокую стоимость метода. Учитывая указанные особенности, СМГК широко используется для анализа ВГ за длительные промежутки времени, а также в больших группах пациентов [11, 12]. При анализе актуальной литературы найдено мало публикаций о компьютерных методиках, оптимизирующих вычисление MAGE на основании данных СМГК. Нами выявлена информация только об одной программе, имеющей функцию расчета MAGE с использованием данных СМГК, – калькуляторе «EasyGV» [13]. В недавней статье авторы EasyGV опубликовали данные о точности показателей ВГ, рассчитываемых с помощью разработанной ими программы [14]. Главным недостатком EasyGV был назван расчет параметра MAGE ввиду проблем в логическом анализе колебаний гликемии, приводящих к неточности вычисления.
Все вышеуказанное привело нас к мысли о создании собственного компьютерного алгоритма расчета MAGE на основании данных СМГК, принципы работы которого базировались бы на оригинальном графическом методе.
Цель исследования: разработать точный компьютерный алгоритм вычисления средней амплитуды гликемических экскурсий на основании данных самостоятельного мониторинга глюкозы крови, оценить эффективность нового алгоритма в сравнении с существующими автоматизированными методами, выполняющими схожие задачи.
Материалы и методы исследования
Алгоритм вычисления MAGE
Нами разработан автоматизированный алгоритм, позволяющий вычислять параметр MAGE на основании данных СМГК. Платформой для его создания послужила программа Microsoft Office Excel 2010. Алгоритм представляет собой цепочку логических формул, с помощью которых поэтапно анализируются данные амплитуд колебаний гликемии, после чего проводится отбор гликемических экскурсий для окончательного расчета MAGE. Исходными данными для вычисления являются: день исследования, время измерения гликемии, уровень гликемии. Введение данных ограничено 12 измерениями за 1 сутки. Дальнейший алгоритм расчета представлен на блок-схеме (рис. 1). Стандартные критерии оценки колебаний гликемии [7] реализуются посредством следующих логических операций: включение в анализ только минимальных и максимальных точек колебаний гликемии с исключением промежуточных; совокупный анализ восходящих и нисходящих сегментов гликемических экскурсий; определение направления первой экскурсии; определение сегмента гликемической экскурсии (восходящего или нисходящего), по которому будет производиться расчет MAGE. Наиболее сложным этапом алгоритма является расчет амплитуды колебаний гликемии со сложной структурой (например, расчет восходящего сегмента экскурсии, состоящего из двух последовательных восходящих отрезков > 1SD и одного нисходящего отрезка между ними < 1 SD). Для решения этой проблемы в нашем алгоритме были применены система поиска стандартных паттернов колебаний гликемии в пределах 12 измерений гликемии в течение суток, а также многоэтапная проверка колебаний гликемии на соответствие условию, согласно которому действительная экскурсия должна превышать 1 SD.
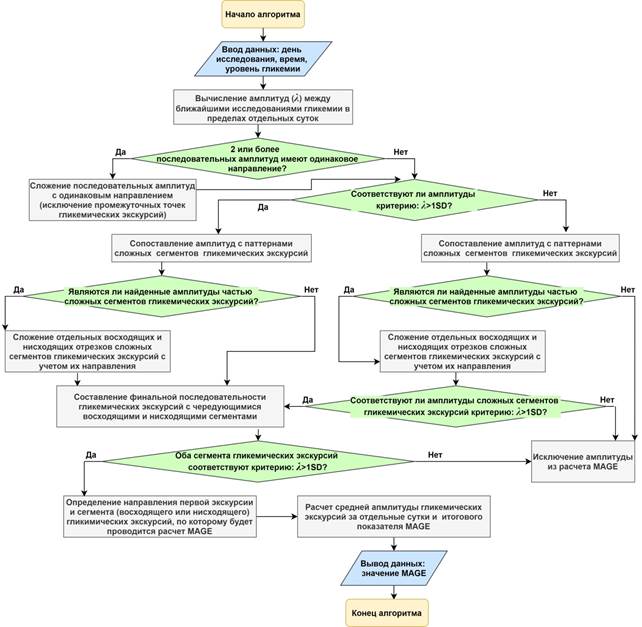
Рис. 1. Блок-схема разработанного компьютерного алгоритма расчета MAGE на основании данных самостоятельного мониторинга глюкозы крови. Условные обозначения: MAGE – средняя амплитуда гликемических экскурсий, λ – величина амплитуды одного сегмента гликемической экскурсии, SD – величина стандартного отклонения глюкозы крови за соответствующие сутки
Оценка эффективности разработанного алгоритма и его сравнение с программой EasyGV
Было выбрано 60 профилей СМГК пациентов с сахарным диабетом из анонимной базы данных результатов обследования ГУЗ «Саратовская городская клиническая больница № 9». Использовались данные самоконтроля, полученные с помощью индивидуальных глюкометров. Критериями отбора СМГК стали следующие параметры: продолжительность СМГК 4–7 дней, частота измерений гликемии 7–12 раз в сутки. Общее количество исследований гликемии, на основании которых проводился дальнейший расчет MAGE, составило 1839.
Первым этапом для каждого из профилей СМГК вручную рассчитан показатель MAGE с помощью оригинального графического метода (MAGE-0). В процессе вычисления учитывались колебания гликемии амплитудой более 1 SD, соблюдены правила расчета по методу F.J. Service и соавт. При расчете первое и последнее колебания гликемии учитывались при условии, согласно которому эти колебания являлись сегментом действительной гликемической экскурсии.
Далее на основании этих же 60 гликемических профилей произведены расчеты параметров MAGE с помощью разработанного компьютерного алгоритма (MAGE-1), а также с помощью программы EasyGV v.9.0.R2 (MAGE-2). Выполнена статистическая оценка согласованности показателей MAGE-1 и MAGE-2 с контрольным методом MAGE-0, проведен сравнительный анализ полученных результатов.
Статистический анализ
Статистическая обработка данных выполнялась с помощью программного обеспечения Microsoft Excel 2010 и IBM SPSS Statistics v.21.0. Для оценки нормальности распределения данных использовался критерий Колмогорова–Смирнова. Данные с нормальным распределением представлены как среднее ± стандартное отклонение (M ± SD). Данные, не подчиняющиеся нормальному распределению, представлены как медиана и межквартильный интервал (Me [Q1;Q3]). Согласованность компьютерных алгоритмов расчета MAGE c контрольным методом изучалась с использованием коэффициента ранговой корреляции Спирмена (r), анализа по методу Блэнда–Альтмана, линейной регрессии для выявления систематической погрешности методов. При проверке статистических гипотез значимым считался уровень p<0,05.
Результаты исследования и их обсуждение
Итоговые значения расчетов MAGE-0, MAGE-1 и MAGE-2 были сгруппированы в 3 ряда измерений параметра MAGE, каждый из которых состоял из 60 значений. Полученные результаты составили: MAGE-0 = 4,34 [3,14;5,87] ммоль/л, MAGE-1 = 4,35 [3,15;5,86] ммоль/л, MAGE-2 = 4,29 [2,88;5,93] ммоль/л. При проведении корреляционного анализа выявлены следующие взаимосвязи между компьютерными методами расчета MAGE и эталонным графическим методом: MAGE-1/MAGE-0: r=0,997, p<0,0001; MAGE-2/ MAGE-0: r=0,906, p<0,0001, построены диаграммы рассеяния (рис. 2, 3).
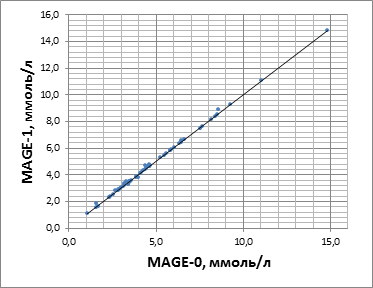
Рис. 2. Взаимосвязь значений средней амплитуды гликемических экскурсий при расчете разработанным компьютерным алгоритмом расчета (MAGE-1) и оригинальным графическим методом (MAGE-0)
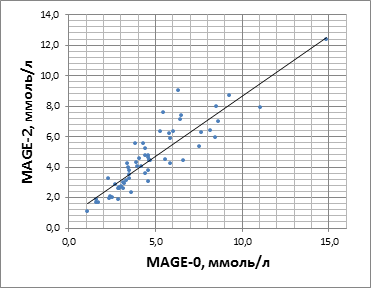
Рис. 3. Взаимосвязь значений средней амплитуды гликемических экскурсий при расчете программой EasyGV (MAGE-2) и оригинальным графическим методом (MAGE-0)
Таким образом, разработанный компьютерный алгоритм расчета MAGE в большей степени коррелировал с контрольным графическим методом по сравнению с программой EasyGV. Коэффициент корреляции Спирмена, приближавшийся к 1, указывал на почти одинаковую точность методов MAGE-1 и MAGE-0.
Для анализа по методу Блэнда–Альтмана исходно вычислены разности и средние значения между каждыми парными значениями MAGE-1 и MAGE-0, MAGE-2 и MAGE-0. Разности MAGE-1/MAGE-0 составили –0,015±0,085 ммоль/л. Разности MAGE-2/MAGE-0 составили 0,24±1,09 ммоль/л. Выполнена проверка отличия полученных разностей от нуля при помощи одновыборочного t-критерия, не выявившая статистической значимости различий (для MAGE-1/ MAGE-0: p=0,166; для MAGE-2/MAGE-0: p=0,093), что подтвердило возможность использования анализа Блэнда–Альтмана. Далее вычислены верхние и нижние границы 95%-ного доверительного интервала по формуле: среднее значение разностей ± (1,96 × стандартное отклонение разностей). Для методов MAGE-1/MAGE-0 верхняя граница 95%-ного доверительного интервала составила 0,15 ммоль/л; нижняя граница: –0,18 ммоль/л. Для методов MAGE-2/MAGE-0 верхняя граница 95%-ного доверительного интервала составила 2,38 ммоль/л; нижняя граница: –1,9 ммоль/л. На основании полученных результатов построены графики Блэнда–Альтмана (рис. 4).
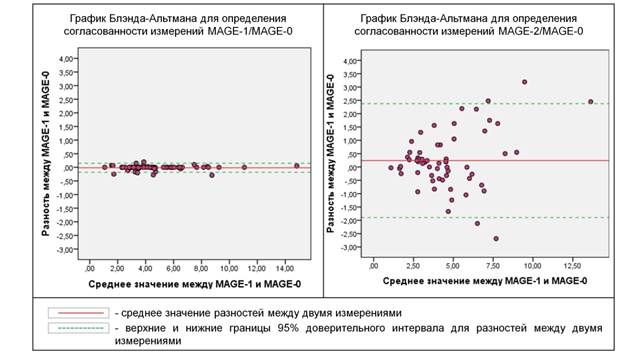
Рис. 4. Сопоставление графиков Блэнда–Альтмана для анализа согласованности компьютерных алгоритмов расчета средней амплитуды гликемических экскурсий с оригинальным графическим методом
При анализе графиков Блэнда–Альтмана выявлено, что средняя разность между значениями MAGE-1 и MAGE-0 приближена к 0, это свидетельствует о хорошей согласованности методов. При сопоставлении значений MAGE-2 и MAGE-0 средняя разность в большей степени отклонялась от 0. Однако в большей степени обращал на себя внимание тот факт, что разности между MAGE-2 и MAGE-0 имели довольно широкий 95%-ный доверительный интервал по сравнению с данными согласованности с MAGE-1/MAGE-0. На графике Блэнда–Альтмана для MAGE-2/MAGE-0 видно, что значения расчетов с помощью калькулятора EasyGV довольно часто отличались от результатов контрольного метода на 1–2 ммоль/л. Такие отличия могут оказывать существенное влияние на оценку вариабельности гликемии у пациента с сахарным диабетом. При сопоставлении MAGE-1 и MAGE-0 95%-ный доверительный интервал, напротив, оказался сравнительно небольшим.
Систематическая погрешность методов определялась с помощью линейной регрессии, в которой зависимой переменной выступала найденная разность между измерениями, а независимой – среднее значение между ними. Коэффициенты примененной регрессионной модели a и b составили для MAGE1 – MAGE0: a = –0,021 (p=0,392); b = 0,001 (p=0,799), для MAGE-2/MAGE-0: a = –0,383 (p=0,227); b = 0,134 (p=0,031). Коэффициент b для MAGE-2/MAGE-0 указал на статистически значимую систематическую погрешность результатов расчета MAGE-2 при сопоставлении с контрольным методом. Для метода MAGE-1 при аналогичном сопоставлении статистически значимой систематической погрешности не было выявлено.
Заключение
Разработанный новый алгоритм расчета MAGE на основании данных СМГК показал высокую степень согласованности с оригинальным графическим методом, предложенным F.J. Service и соавторами. На основании проведенного сравнительного исследования показано, что наш алгоритм превосходит существующую программу EasyGV по функции расчета MAGE. Мы планируем продолжить работу над совершенствованием предлагаемого автоматизированного алгоритма и разработкой полноценной компьютерной программы для оценки вариабельности гликемии на основании результатов самоконтроля у пациентов с сахарным диабетом. Такая программа даст возможность врачам-эндокринологам в амбулаторных и стационарных условиях быстро и точно оценивать степень вариабельности гликемии, основываясь на данных простого и доступного метода – самостоятельного мониторинга глюкозы крови. Кроме этого, указанный алгоритм позволит определять показания для более детального, но ресурсозатратного исследования – непрерывного мониторирования глюкозы. Таким образом, точные автоматизированные методы будут способствовать улучшению качества гликемического контроля у пациентов с сахарным диабетом. Подводя итог сказанному, следует заметить, что компьютерная оценка вариабельности гликемии является перспективным направлением в области современной диабетологии.



