В настоящее время одной из серьезнейших задач образования является снижение уровня творческой активности обучающихся как в среднем, так и в высшем звене. Переход на тестовую проверку знаний – Основной государственный экзамен в 9-м классе средней школы, Единый государственный экзамен в 11-м классе, балльно-рейтинговая система в вузе – все это в некоторой степени снижает творческую активность школьников и студентов, поскольку основная задача сводится к умению выполнить тестовое задание, а не научиться решать те или иные задачи. Другими словами, современного учащегося учат зазубриванию материала и поиску готовых решений вместо умения думать своей головой и решать задачи самостоятельно. Сам механизм образовательной системы поощряет учащихся за качественное вспоминание полученных знаний, но не за собственные идеи. Если упростить, то современная образовательная система учит зубрить, а не думать, в то время как современные блага цивилизации в виде Интернета и цифровых устройств разрушают базовые интеллектуальные способности среднестатистического учащегося, такие как концентрация внимания. В результате мы получаем человека, не умеющего качественно адаптироваться в жизни из-за неспособности решить свои собственные жизненные задачи и ожидающего готовых ответов, подобно тому, как этот процесс происходил в учебном заведении.
Ретроспективный анализ собственной деятельности показывает, что современные школьники акцентируют внимание на решении прототипов задач по шаблону. Смысл заключается в том, чтобы отработать алгоритмы и решить как можно больше прототипов заданий. В итоге получается, что, если задачи на экзамене несколько отличаются от решаемых ранее, ученики часто заходят в тупик и не знают, что делать. Это говорит о неразвитости творческого потенциала школьников. Другими словами, они теряются, когда нужно придумать идею самостоятельно. Им требуются готовые решения, которые учащиеся желают получить из уст учителя либо на каком-либо интернет-ресурсе.
Одной из главных причин такого положения является отсутствие целостной теории сознания вообще. В психологии не имеется единой методологической платформы для изучения мозговых процессов. В современной психологической науке выделяются по меньшей мере четыре парадигмы: бихевиористская, психоаналитическая, гуманистическая и системно-деятельностная, каждая из которых характеризуется своими методами и обладает специфическими особенностями. Это ведет к тому, что в процессе обучения не всегда выявляются, а тем более проявляются потенциальные возможности обучающихся, а говорить о формировании творческого мышления вообще не приходится. Вместе с тем, по мнению Е.Е. Верхотурцевой: «Развитие творческого мышления должно быть направлено не на выявление и развитие одаренных детей, а на оптимизацию мышления с целью его вывода на высший уровень – творческий» [1].
Поэтому не случайно в современной педагогической науке появляется много разнообразных подходов к изучению данного феномена. Х.Ш. Абдуллаева пишет: «Творческое мышление характеризуется максимальной свободой в преодолении пространства и времени и в оперировании ими при решении конкретных задач, оно является максимально синтетичным, максимально обобщенным по отношению к конкретным образам и сенсорным переживаниям и основано на максимальной субъективной активации, без которой оно вообще не может развертываться» [2]. По мнению А.А. Матюшкиной и М.Б. Чечельницкой, «…критерием творческого мышления выступает наличие новообразований в деятельности по решению задачи субъектом – новых мотивов, целей, смыслов» [3].
В данной статье основной целью является анализ возможностей формирования творческих способностей учащихся (как проявление творческого мышления) на основе использования методов, разработанных в Международной академии траблхакинга. Сам термин «траблхакинг» происходит от английского trouble – «проблема, неприятность» и hacking – «взлом, поиск лазеек». Это методология совершенствования систем, набор методов и средств, направленных на изобретение нестандартных путей решения задач и применение их на практике [4].
Материал и методы исследования. Суть методов траблхакинга состоит в попытке проанализировать задачу как систему, описав механизм взаимодействия подсистем с надсистемами, и уже на основе этих данных траблхакинг позволяет усовершенствовать систему целиком, решив поставленную задачу. Помимо прочего, задача раскладывается на этапы и подзадачи, а далее уже внутри подзадач анализируются взаимоотношения частей общей системы. Возникает вопрос: зачем проводить столь глубокий анализ? Дело в том, что мы ищем «точки воздействия» на элементы системы и, основываясь на них, изобретаем креативные идеи. Таким образом, создание нового может превратиться из спонтанного процесса в четко сформулированный набор шагов, которому довольно просто обучить школьников и студентов. Для проведения описанного выше процесса создания креативных идей в траблхакинге имеются два метода: алгоритм эффективного решения проблем (АЭРП) и алгоритм «Вектор». Первый состоит из тринадцати шагов, второй – из восьми [5].
АЭРП – это базовый метод траблхакинга, позволяющий путем глубокого анализа нетехнических систем изобрести нестандартные способы решения задач и применить их на практике. Алгоритм основан на системном анализе, теории рисков и инструментах Теории решения изобретательских задач (ТРИЗ). Достоинством ТРИЗ являются разработка и использование на практике алгоритмизированных методик, позволяющих сколь угодно сложную задачу разложить на простые подзадачи, решение которых оказывается настолько простым, что даже слабые учащиеся в состоянии это сделать. Другими словами, решение сложной задачи сводится к строгому следованию алгоритмам, что позволит начинать решение не с ответа на вопрос, который не всегда очевиден, а с поиска способов упрощения начальной сложной задачи, разложения ее на отдельные составляющие, что в конечном итоге приведет к ответу на поставленный вопрос. Еще одним важным аспектом при таком методологическом подходе является умение не следовать шаблонными путями, а искать нестандартные способы решения проблем.
Алгоритм «Вектор» – это упрощенный метод траблхакинга, целями которого являются изобретение эффективных способов решения задач и применение их на практике. Метод основан на запуске ассоциативного мышления через анализ Реестра изобретательских идей траблхакинга, который представляет собой программный комплекс, содержащий в себе структурированный набор идей, направляющих вектор размышлений траблхакера на повышение идеальности систем – максимальную реализацию ядра цели с минимальными затратами.
В качестве примеров того, как методы или части методов траблхакинга возможно использовать в педагогической науке, приведем алгоритмы решения задач из школьной математики, что может быть актуально и для школьников, и для студентов, и особенно для будущих учителей. Как отмечается в работе К.Н. Лунгу: «Средствами математики можно формировать и развивать большой набор способностей и качеств молодого человека, что особенно важно в наш век становления нового информационного общества» [6]. Но данные подходы можно использовать и при изучении любых предметов. Здесь необходимо обратить внимание на два аспекта:
1) умение разложить на подзадачи любую сложную проблему и выделить знания, необходимые для решения отдельных подзадач;
2) на основе более общих знаний найти более простые пути достижения цели, особенно для нестандартных частных случаев.
Результаты исследования и их обсуждение. Математика является одной из наиболее строгих логически алгоритмизированных наук, в которой ученые имеют дело с идеальными объектами, подчиняющимися строгим правилам. Тем не менее даже в этой абстрактной науке существуют возможности нестандартных способов решения задач, что способствует развитию творческого потенциала учащихся.
Рассмотрим пример решения тригонометрического уравнения: 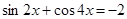 . Шаблонное решение выглядит так. Используем формулу двойного угла:
. Шаблонное решение выглядит так. Используем формулу двойного угла: 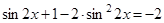 . Получим квадратное уравнение:
. Получим квадратное уравнение: 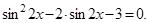 ‚ ведем новую переменную:
‚ ведем новую переменную: 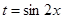 . Имеем:
. Имеем: 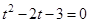 . ‚ вычислим дискриминант и корни уравнениЯ:
. ‚ вычислим дискриминант и корни уравнениЯ: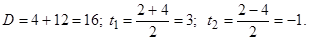 Первый корень больше 1, поэтому не является решением.
Первый корень больше 1, поэтому не является решением. 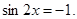
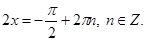 Отсюда
Отсюда 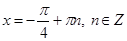 .
.
Если разложить данное решение на знания, необходимые для решения отдельных подзадач, будем иметь:
1) формулы двойного угла функций синуса и косинуса;
2) решение тригонометрических уравнений методом замены;
3) решение квадратного уравнениЯ;
4) область значений функций синуса и косинуса;
5) формулы частных случаев решениЯ тригонометрических уравнений.
Но, если вспомнить область определениЯ синуса и косинуса и учесть, что минимальное значение этих функций равно Р1, можно сразу получить систему уравнений: 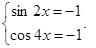
Решая каждое уравнение в отдельности и находя пересечение промежутков решения обоих уравнений, будем иметь: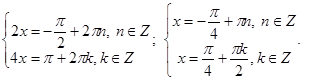
Решение системы будет совпадать с решением первого уравнения, так как решения второго уравнения полностью включают в себя решения первого: 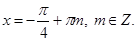
Џри таком решении знаниЯ, необходимые длЯ решениЯ отдельных подзадач, будут следующие:
1) область значений функций синуса и косинуса;
2) элементарные правила сложениЯ;
3) формулы частных случаев решениЯ тригонометрических уравнений.
При таком решении знания, необходимые для решения отдельных подзадач, будут следующие:
1) область значений функций синуса и косинуса;
2) элементарные правила сложения;
3) формулы частных случаев решения тригонометрических уравнений.
Простота и легкость второго способа решения очевидны. Говоря терминологией траблхакинга: мы усовершенствовали систему, решив задачу более эффективным образом, путем более глубокого анализа и выявления частей, на которые можно воздействовать. Здесь важно не только сокращение подзадач, но и их содержание. Элементарные правила сложения заменяют три более сложные подзадачи.
Более наглядный пример. Решить уравнение: 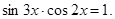 Стандартный прием. Необходимо свести уравнение к одинаковому аргументу и к одной функции. Используем формулы тройного и двойного угла:
Стандартный прием. Необходимо свести уравнение к одинаковому аргументу и к одной функции. Используем формулы тройного и двойного угла: 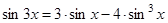 и
и 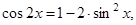 получим:
получим: 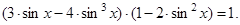 Раскрывая скобки и приводя подобные слагаемые, будем иметь:
Раскрывая скобки и приводя подобные слагаемые, будем иметь: 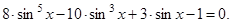 Введем новую переменную:
Введем новую переменную: 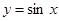 , получим уравнение пятой степени
, получим уравнение пятой степени 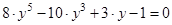 ,
,
которое не решается в общем виде. В итоге ученики заходят в тупик, начальная задача представляется неразрешимой. В данной ситуации наиболее сильные учащиеся смогут придумать способ решить это уравнение методом группировки, или методом подбора, или же через исследование функции путем вычисления производной, нахождения точек экстремума, промежутков монотонности. Это возможно сделать только потому, что при приравнивании производной к нулю получается биквадратное уравнение, которое легко решается. Однако в общем случае это не всегда возможно.
Тем не менее здесь можно выделить знания, необходимые для решения отдельных подзадач:
1) формулы двойного и тройного угла функций синуса и косинуса;
2) решение тригонометрических уравнений методом замены;
3) решение уравнения пятой степени (этот пункт может включать в себя еще три-четыре подзадачи в зависимости от выбора способа решения);
4) область значений функций синуса и косинуса;
5) формулы частных случаев решения тригонометрических уравнений.
Здесь уже на третьей подзадаче школьник сталкивается с непреодолимыми трудностями. Однако, если сообразить, что произведение синуса и косинуса равно единице только тогда, когда обе функции принимают максимальное значение, равное 1, или минимальное значение, равное –1, получаем две системы уравнений.
В первом случае: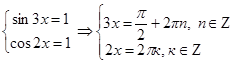 ;
; 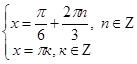 .
.
Решением данной системы является пустое множество.
Во втором случае: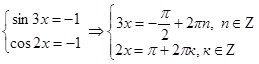
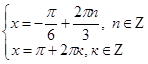 .
.
Пересечение решений даст значение 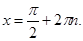 кто и будет общий ответ.
кто и будет общий ответ.
Знания, необходимые для решения отдельных подзадач, в данном случае будут следующие:
1) область значений функций синуса и косинуса;
2) элементарные правила умножения;
3) формулы частных случаев решения тригонометрических уравнений.
Здесь так же очевидны простота и легкость второго способа решения. Другими словами, решение стало более совершенным.
Приведенные примеры могут использоваться учащимися средней школы при подготовке к экзаменам, олимпиадам по математике, а умение выделить знания, необходимые для решения отдельных подзадач, особенно актуально при изучении дисциплины «Методика преподавания математики» в педагогических университетах и институтах.
Понятно, что не любую задачу можно упростить, тем более что математика как наиболее алгоритмизированная наука чаще всего использует строгие, неизменяющиеся правила. Но даже в математических задачах возможны разнообразные нестандартные ходы, что позволяет развивать творческое мышление учащихся. В других учебных дисциплинах таких возможностей еще больше. И здесь получается некая парадоксальная ситуация: чем сложнее проблема, тем больше способов ее решения. Но, чтобы увидеть эти способы, необходимо проанализировать сам механизм задачи и найти в нем составные части, которые возможно упростить и усовершенствовать. Часто для этого достаточно разложить сложную задачу на элементарные и независимо от их количества проанализировать их как общую систему, удерживая в голове стремление избавить рассматриваемую систему от минусов, упростить ее и сделать более совершенной. Нам нужна последовательность действий, где каждый шаг следует за предыдущим. Таким образом, мы получаем список этапов, в каждом из которых есть свое ядро подцели (подзадачи). Ядро подцели – это то же самое, что ядро цели, только относительно этапа. Ядро последней подцели является итоговым результатом. Этапы нужны нам, чтобы выделить из них элементы, на которые можно будет воздействовать для получения итогового результата. Стоит понимать, что мы не составляем план действий для ежедневника, а ищем точки воздействия, спрятанные в этапах. Поэтому нам достаточно самых очевидных и простых шагов. Для всего вышесказанного в траблхакинге имеется масса инструментов, применимых в широком спектре задач (например, анализ помех, проектирование идеального состояния систем и списки доступных ресурсов).
Заключение. Таким образом, использование методов траблхакинга позволяет алгоритмизировать творчество, превратить процесс создания нового в последовательность шагов, которым легко научить большую массу учащихся. И, если раньше считалось, что высокую творческую активность могут проявлять лишь талантливые люди, которые имеют эту способность от природы, то теперь методы траблхакинга позволяют сделать универсального изобретателя из любого человека. Но главная особенность методов траблхакинга состоит в широком спектре решения задач. Ученик, владеющий методами траблхакинга, может анализировать личные жизненные задачи, бизнес-задачи и даже глобальные общественные проблемы [7]. Траблхакинг – это не просто новое научное направление или профессия будущего. Миссия траблхакера – совершенствование систем, совершенствование себя, сфер своей жизни, общества, мира. Таким образом, путем внедрения методов траблхакинга в образовательную программу мы не только решим проблемы заучивания и неумения думать своей головой, но и научим человека решать свои жизненные задачи. Мы получим новое поколение открывателей, способных создавать новое, успешно адаптироваться в жизни и делать нашу страну лучше.



