Современное общество достигло такого уровня развития, что для полноценной педагогической деятельности будущим учителям необходимо использовать приемы логико-вариативного мышления, основу которого представляют логические и стохастические знания. Поэтому на математических факультетах вузов, участвующих в подготовке специалистов по направлению «Педагогическое образование», одной из изучаемых фундаментальных дисциплин является стохастика. Эта дисциплина позволяет формировать вероятностно-статистическое мышление, дающее возможность использовать приемы логического мышления в условиях четкости терминологии, конкретности понятий и неопределенности.
Цель исследования: обоснование подходов к реализации вероятностно-статистического содержания в подготовке учителя математики и соответствующей методике обучения.
Методы исследования. Обзор соответствующей научно-методической литературы, стандартов образования. Применение в ходе работы компетентностного, личностно ориентированного, системного подходов, моделирования.
Результаты исследования и их обсуждение. Совершенствование подготовки учителей – актуальная проблема системы отечественного высшего образования. Нами исследовалась ранее проблема реализации инновационных процессов в высшем образовании в аспекте экономической интеграции [1]. Для развития инновационного содержания образования одной из главных компонент становятся стохастические знания, они необходимы как для познания вероятностного характера явлений окружающего мира, так и для развития самого субъекта образовательной деятельности. Будущему учителю необходимо развивать стохастическую интуицию и овладеть методологией, использующей стохастические умозаключения, то есть приоритетное значение при обучении стохастике отводится воспитанию стохастической культуры студентов [2]. При этом целостность как структурная, так и содержательная должна стать главным принципом выстраивания стохастического курса. Излагаемый материал по этому направлению для студентов университетов и пединститутов представлен в настоящее время двумя существенно отличающимися подходами. Обозначим первый подход как прикладной. Он ближе к интуитивному пониманию предмета студентами, так как обращается к экспериментам, играм, носящим модельный характер для описания случайных событий (игральные карты, лотерея, подбрасывание наугад различных предметов – монет, игральных костей). Однако уровень развития интуиции у студентов может существенно различаться, что зачастую приводит к парадоксальным результатам и выводам при решении задач, что заставляет сомневаться в целесообразности использования данного подхода [3; 4]. Например, при случайном подбрасывании двух игральных кубиков необходимо определить вероятность выпадения цифр на каждом из кубиков, дающих в сумме: а) 9; б) 10. Для случая а) это могут быть пары чисел (3,6) и (4,5). Для случая б) также две пары чисел - (5,5), (5,5). Для определенности пусть 3 и 4 – числа, выпавшие на первой кости, а 6 и 5 – на второй кости. На интуитивном уровне для многих игроков равенство числа указанных пар чисел (способов), при которых произойдут интересующие события, означает, что вероятности выигрыша равны. Однако в такой ситуации интуиция ошибается. Берем круг радиуса R и наудачу выбираем хорду. При нахождении вероятности события «для равностороннего треугольника, вписанного в этот круг, длина хорды больше длины его стороны» получаем соответственно числа 1/2 или 1/3 или 1/4, так как интуиция отвечает на слова «случайно взятая хорда» неодинаково для различных исследователей [3; 4].
Поучителен следующий пример, приводящий студентов к ошибочным выводам при опоре на интуицию. Предлагаем студентам игру: возьмем три карточки, на одной из них изображена цифра 1 с обеих сторон, на второй – цифра 2 тоже с обеих сторон. А на третьей карточке с одной стороны изображена цифра 1, а с другой – цифра 2. Студент наугад берет карточку и у него выпадает на видимой им стороне карточки цифра 1. Ему необходимо определить шанс события: цифра 1 изображена и на другой стороне карточки. Как правило, студенты ошибочно оценивают вероятность, равной 1/2. Верный ответ 2/3, так как надо учитывать случайный выбор и карточки, и ее стороны.
Второй подход – теоретико-множественный, наиболее принят в классическом преподавании, опирается на абстрактную теорию вероятностей и аксиоматический метод. Он оправдан при решении проблем и задач, в которых математическая формализация – единственный способ решения, так как практически невозможно построить вероятностную модель. Применяется в связи с интерпретацией наиболее фундаментальных свойств пространства вероятностей [4]. Для этого аксиоматического подхода основным недостатком является потеря связи с интуицией в представлении знаний о вероятностях появления событий, причем при проведении конкретного эксперимента невозможно вычислить значения вероятностей случайных событий [4]. При решении прикладных задач усвоившие такой курс студенты, как правило, совершенно беспомощны. Поэтому при обучении студентов стохастике целесообразно использовать оба подхода. Это обусловлено тем, что стохастическая линия отражает внутреннее единство теоретической и эмпирической ступеней познания мира случайностей.
Приоритетная роль при обучении студентов, очевидно, принадлежит методике преподавания этой ветви высшей математики. Она, выбранная правильно, раскрывает особенности изучения данного предмета, способствует формированию у студентов базовых знаний, поиску рациональных способов решения прикладных задач, гарантирует специфику обучения фундамента науки [5, с. 416]. Отметим, что в современных условиях использование компьютера при обучении дает возможность расширения диапазона применяемых в учебном процессе методик, способствует улучшению способов проверки выполнения заданий, налаживанию связи со студентами, реагированию на проблемные ситуации, появляющиеся при изучении стохастики [6]. Например, у одного кубика число очков на гранях: 0, 1, 2, 4, 5, 6; у другого – 1, 1, 1, 4, 4, 4. Студент первым выбирает кубик, которым будет играть. Компьютеру достается другой кубик. Студент получает 1 очко, если на его кубике при подбрасывании на грани появится число больше, чем у второго игрока (компьютера). Очки суммируются. Возникает вопрос, какой кубик следует выбрать студенту для победы? Для ответа смоделируем бросание двух таких кубиков в MS Excel. Число бросков возьмем равное, например, 6000. Ниже (рис. 1) представлена часть листа с вычислениями и диаграммой, которая подсказывает: выбрать следует первый кубик.
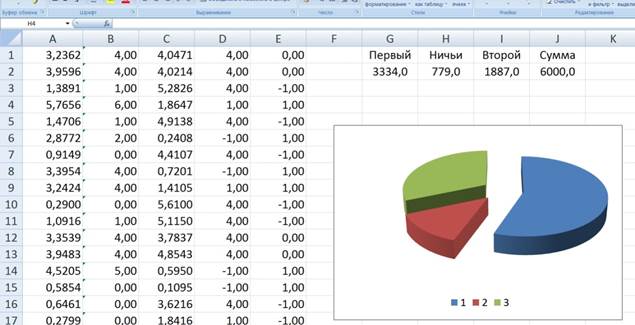
Рис. 1. Часть листа с вычислениями и диаграммой
Изучение стохастики желательно начинать с исторического обзора, остановившись на следующих разделах теории вероятностей: стимулы возникновения: первый период становления; развитие до середины XIX века; работы Петербургской школы; современный период развития [7]. Стохастические понятия преподаватель должен вводить не абстрактно, а в соответствии с тем естественным путем, который способствовал их появлению. Необходимо обучить студентов видеть в них живое содержание, а в окружающих объектах обнаруживать стохастическую структуру. Для развития системы базовых понятий и интуиции необходимо на занятиях по стохастике создавать творческую атмосферу: обсуждать, размышлять, спорить, применяя нестандартные подходы. Например, предложить студентам почувствовать следующую стохастическую неожиданность. Из 52 карт откладываем в сторону 4 короля. Каждый из четырех игроков получает 12 карт одной масти и после их перетасовки выкладывает на стол одну. Игроки с красными картами образуют команду «красных», игроки с черными картами команду «черных». Далее важно только значение карты. Если среди выложенных карт окажутся хотя бы две одинаковые карты (событие А), то побеждает команда «черных», если такое не произойдет, побеждает команда «красных». Предлагается оценить шансы обеих команд. Очевидным кажется, что шансы у команды «черных» намного больше. Чтобы проверить это интуитивное суждение, можно на первом этапе сослаться на эмпирические данные. В группах по четыре человека повторять игру и заметить, что почти в половине состязаний побеждает команда «красных». Следовательно, неожиданный факт нуждается в объяснении математическими средствами.
Поэтому студентам предлагается найти вероятность этого события и убедиться, что P (A) ≈ 0, 43. Естественно в такой ситуации они имеют дело с особым видом мотивации, состоящей в желании понять то, что для них показалось неожиданным.
Абстрактное изложение теории вероятностей позволяет ускорить процесс подведения будущих учителей к современному состоянию науки. Однако желательно при первоначальном знакомстве со стохастикой рассматривать больше примеров, способствующих развитию стохастической интуиции, которая от природы развита плохо. Например, полезно рассмотреть следующую задачу. В полицию поступило сообщение: у частного предпринимателя совершена кража денег путем взлома сейфа. Случайные прохожие заметили подозрительных личностей, которые спешно садились в автобус, следовавший из села в город. Полиция сразу же была информирована об этом. Автобус остановила автоинспекция при въезде в город, причем следователь запретил выпускать пассажиров. Шофер уведомил следователя, что в автобусе находится 40 пассажиров, он волновался в связи с задержкой рейса. Следователь сократил время обыска, предложив только наугад выбранным шести пассажирам покинуть автобус. Один из похитителей был сразу найден, так как в его кармане была обнаружена пачка денег. Он тут же выдал сообщников. Необходимо ответить, из чего исходил следователь при выборе числа досматриваемых пассажиров – риска или трезвого расчета [8]?
Кроме того, преподаватель не должен откладывать в сторону примеры практического использования методов стохастики для различных ситуаций окружающей действительности. Например, на примере страхования автотранспорта указать на связь частот и вероятностей. Для того чтобы решить: кто и сколько по справедливости должен платить, необходимо учитывать два обстоятельства: а) вероятность автомобиля попасть в аварию; б) средний ущерб окружающим от одной аварии [9].
Не вызывает сомнения, что для развития математической деятельности, успешного усвоения теории, практических умений, методов и различных приложений стохастики одной из наиболее эффективных форм является решение прикладных задач. Представим, что на заводе, производящем тракторы определенной модели, не каждый соответствует требованиям заказчика. Поэтому руководство предприятия, как правило, планирует выпустить заведомо большее количество тракторов. Допустим, что заказ получен на 90 тракторов, а запланировано 100. Студентам предлагается определить вероятность полного выполнения заказа, если вероятность производства каждого назначенного трактора по заказу, соответствующего требованиям заказчика, равна 0,9. И на основании полученной информации об этом событии пояснить: какие выводы должно сделать руководство завода?
С учетом планирования выпуска десяти тракторов сверх заказа вероятность полного его выполнения, полученная с помощью интегральной теоремы Лапласа, оказалась небольшая – 0,5. Вывод: увеличение количества тракторов нецелесообразно, нужно добиваться того, чтобы каждый трактор соответствовал требованиям заказчика.
Необходимо убедить студента, что стохастическая теория возникает из практики и в процессе своего дальнейшего развития постоянно обращается к ней. Оценка вероятностей производится в самых различных областях профессиональной деятельности, как при оценке вероятности распространения эпидемии до уровня пандемии и необходимости планирования срочной массовой вакцинации, так и при принятии решения о качестве выпускаемой продукции на основании выборочных данных. Для нефтедобывающих стран при составлении бюджета государства важна информация о цене на нефть. Предвидеть эти цены безошибочно не удается.
При изучении стохастики преподаватель должен не только изложить сведения об этой дисциплине, но и заострить внимание студентов на ее связи с другими разделами математики. Очевидно, межпредметные связи отображает система задач, которые в достаточной мере соответствуют целям изучения вероятностных моделей. Межпредметные связи в теоретическом плане заложены в самой научной области курса стохастики. Обладая собственным предметом изучения, она одновременно опирается на данные других учебных курсов («Логика», «Математический анализ», «Линейная алгебра» и др.), следовательно, является одновременно источником знаний и их потребителем. Процесс реализации стохастической линии можно представить как определенную систему, в которой одновременно происходит дифференциация и интеграция содержания обучения. Однако в действительности появляется противоречие между традиционной системой стохастической подготовки учителя и возможностью применения интегративного подхода. На лекциях преподаватель экономит время на общие рассуждения, выявление истоков дисциплины, существующие связи между задачами практики и стохастики. А это способствует тому, что многие студенты не понимают тонкости в логических построениях курса и воспринимают эту дисциплину формально [10]. В то же время реализация интегративного подхода преподавания стохастики будущим учителям позволяет достигнуть: формирования стохастической культуры; научного мировоззрения; профессионального мышления; выработки учебных, исследовательских, коммуникативных и многих других умений. Чаще всего в педагогической практике при обучении стохастике используют следующие методы: словесные, наглядные, практические, интерактивные и другие [4]. Например, при практическом методе можно провести с 30 или даже с 40 студентами игру «Жизнь или смерть». Один властелин решил казнить звездочета, который наскучил своими ложными предсказаниями. Но позволил разложить ему два черных и два белых шара по двум урнам. Палач выберет шар из одной наугад взятой урны. Звездочета казнят при появлении черного шара; в противном случае он останется жить. Каким образом звездочет должен разложить шары по урнам, чтобы о6еспечить максимальную возможность уцелеть? Убедившись, как проявила себя, «поработала» вероятность, необходимо подсказать звездочету ответ. Кроме того, студентам предлагается найти ответ на этот вопрос при различных вариантах размещения шаров по урнам; продемонстрировать один из таких вариантов решения задачи, используя компьютерные технологии. Например, взять 4 урны и размещать в них 7 белых и 7 черных шаров.
Максимальной эвристической силой при обучении стохастике являются интерактивные методы [11]. В частности, применение компетентностно-ориентированных задач, которые наиболее соответствуют формированию соответствующих компетенций при подготовке будущих учителей [12]. Например, студентам можно предложить следующую задачу. Ежесуточный расход бензина определенной марки в некоторой транспортной фирме является случайным с mx = 110 т σx = 30 т. Расход бензина в разные дни представляют взаимно независимые величины. Поставка бензина происходит один раз в месяц. Оценить шанс того, что имеющийся вначале запас в 3500 т будет достаточен на месяц (30 дней). А также найти ответ на вопрос, каким должен быть запас бензина, чтобы с вероятностью 0,95 его хватило фирме для работы. Очевидно, расход бензина за месяц есть случайная величина Y = X +X + … + X, где все слагаемые имеют одинаковый закон распределения и взаимно независимы. Можно считать, что 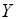 имеет приближенно нормальный закон распределения, что позволяет быстро найти ответ на первый вопрос задачи. А все промежуточные вычисления для ответа на второй вопрос студенты могут выполнить в свободно распространяемом пакете Maxima и получить m ≈ 3570, 2770.
имеет приближенно нормальный закон распределения, что позволяет быстро найти ответ на первый вопрос задачи. А все промежуточные вычисления для ответа на второй вопрос студенты могут выполнить в свободно распространяемом пакете Maxima и получить m ≈ 3570, 2770.
Необходимо подчеркнуть, что многие будущие учителя математики не обладают необходимым уровнем стохастической подготовки и вероятностным мышлением. Они теряются при решении даже не слишком сложных задач, возникающих в жизни при оценке вероятностей случайных явлений, требующих понимания специфики вероятностных умозаключений и прогностических выводов. Учитывая важность компьютерных технологий в подготовке современных педагогов, рекомендуем, помимо интеграции теоретико-множественного и прикладного подходов в обучении стохастике, использовать пакеты программ: Mathematica, MathCad, Excel, Statistica, SPSS, Stadia. Выгодно также использовать свободно реализуемые программы: Maxima, GeoGebra, R, RapidMiner, Dataplot, StatistX, Gretl и другие.



