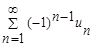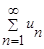Обучение математике студентов в вузе – сложный и многогранный процесс, сравнимый с огромным механизмом, наделенный свойствами многофункциональности, технологичности и мощности. Сложность и многогранность его заключаются, с одной стороны, в специфичности самой дисциплины математики как таковой (не зря еще со школы большая часть учеников испытывают трудности в изучении именно данного предмета), с другой – в методике ее преподавания, где главную роль играет профессиональная компетентность учителя/преподавателя. Многофункциональность механизма объясняется единым исполнением функций образования, воспитания и развития обучающихся. Отсюда вытекает еще одно его свойство – технологичность, поскольку в результате процесса обучения мы получаем совершенно новую, профессионально развитую личность, обладающую знаниями, умениями, навыками, необходимыми для успешного решения профессиональных задач.

Проблема повышения математической культуры в вузе, как, впрочем, и в школе, главным образом связана с несоответствием методики преподавания данной дисциплины с индивидуальными особенностями студентов, а именно с несоответствием у них типов мышления. Другими словами, человек, у которого развито наглядно-образное мышление, испытывает трудности в понимании абстрактных определений математических терминов. Многолетняя практика преподавания в вузе констатирует тот факт, что единая методика преподавания той или иной математической теории распространяется на всю академическую группу студентов, независимо от их типа мышления, и зачастую даже не изменяется со временем, в плане структуры. Отсюда и возникает проблема в восприятии информации, то есть происходит разрыв звеньев одной цепи построения логической связи между субъектом и предметом восприятия информации.

Целью настоящего исследования является: разработать различные подходы построения методологии обучения математике, соответствующие типу мышления обучающихся.

Материалы и методы исследования. Данное исследование проводилось на основании научных материалов ученых, занимающихся вопросами преподавания математики в высшей школе. Экспериментальная часть работы посвящена теме определения типа мышления с помощью психологического тестирования (в модификации Г.В. Резапкиной) [1].

По мнению В.А. Иванникова, понятие мышления рассматривается на двух платформах: 1) самонаблюдение с переживанием человеком активности сознания и переживание «я думаю»; 2) способность человека строить понятийную картину мира, то есть решать познавательные задачи. В этом случае мышление вводится как теоретический конструкт (концепт) [2, с. 285].

Цель изучения математики в вузе – повышение математической грамотности, культуры студентов, развития логического мышления, творческих способностей, умения находить пути решения в нестандартных ситуациях.

По словам Е.А Максимовой, антропологический подход к профессиональному образованию есть, по сути, определение цели и содержания образования, способов его организации, специфики взаимодействия субъектов через призму индивидуальных потребностей, интересов и запросов студентов [3, с. 65].

«Ключевыми аспектами обучения математике», – отмечает И.А. Байгушева, – являются: понятийная обеспеченность всех предметных образовательных действий, понимание всех необходимых, существенных, устойчивых и воспроизводимых причинно-следственных связей – теорем и эквивалентных им суждений, универсальный подход к решению любых задач» [4, с. 33].

Диагностика определения типа мышления у студентов проводилась на основе опрос–теста по методике в модификации Г.В. Резапкиной, включающего в себя 40 вопросов. В данном опросе приняли участие 65 студентов 1 курса очной формы обучения инженерных и биологических направлений ФГБОУ ВО «Иркутский государственный аграрный университет им. А.А. Ежевского». Результаты опроса представлены в таблице 1.

Таблица 1

Результаты опрос-теста на определение типа мышления по методике Г.В. Резапкиной

В данной версии опросника типы мышления уточнены в соответствии с имеющимися классификациями (предметно-действенное, абстрактно-символическое, словесно-логическое, наглядно-образное; творческое (или креативное)).

Приведем краткую характеристику каждого типа мышления (табл. 2).

Таблица 2

Краткая характеристика типов мышления

Из данной таблицы 1 видно, что:

1) у человека может преобладать несколько типов мышления;

2) обладая несколькими типами мышления, он может являться высоко творческой личностью;

3) у большинства респондентов наблюдается средний уровень развития по каждому типу мышления (рис. 1).

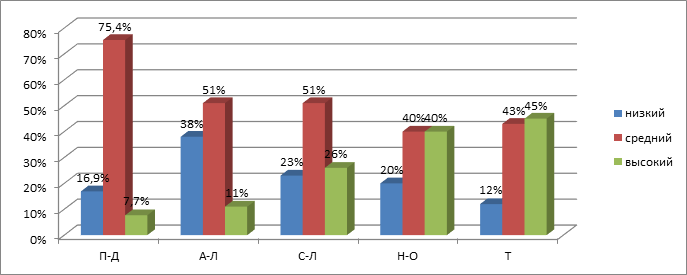
Рис. 1. Уровни развития типов мышления по 65 респондентам

На рисунках 2-4 представлены уровни развития типов мышления студентов 1 курса очной формы обучения направлений бакалавриата ИрГАУ.

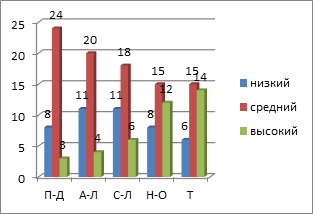
Рис. 2. Уровни развития типов мышления студентов направлений ТТ+ЭЭ+АИ (ЭФ)

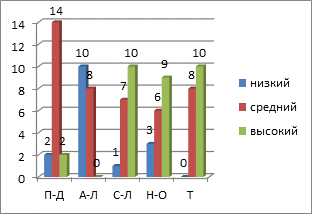
Рис. 3. Уровни развития типов мышления студентов направления ПО

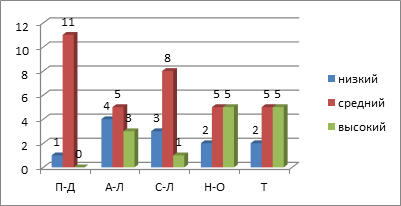
Рис. 4. Уровни развития типов мышления студентов направлений АА+А

Для эффективного освоения лекционного материала по дисциплине «Математика» студентам предлагались три «модели» подачи информации, которые классифицированы по трем видам: 1) алгоритмическая; 2) графическая; 3) абстрактная.

Итак, рассмотрим каждую модель по отдельности.

«Алгоритмическая модель» подачи информации представляет собой словесное правило выполнения того или иного действия, выраженное в последовательности следующих друг за другом шагов при выполнении определенных условий.

Существует множество определений понятия алгоритма, но автор данной работы придерживается определения алгоритма, данного В.Ф. Мелехиным [5, с. 10]: «Алгоритм – набор предписаний, однозначно определяющий содержание и последовательность выполнения действий для систематического решения задачи. Для алгоритма можно выделить семь характеризующих его параметров: совокупность возможных исходных данных, совокупность возможных результатов, совокупность возможных промежуточных результатов, правило начала процесса обработки данных, правило непосредственной обработки, правило окончания процесса, правило извлечения результата».

Как известно, в педагогической литературе один из подходов в обучении, акцентирующий внимание на познавательной активности при помощи наглядности, называется когнитивно-визуальным. Исследователи данной проблемы Вакульчик В.С., Мателенок А.П. считают, что графические схемы дают наглядное представление о системе учебного материала, являются специальным эффективным методическим средством в познавательной активности студентов [6, с. 84].

«Графическая модель» – это наглядная презентация информации, представленная в виде рисунков, графиков, чертежей, диаграмм, блок-схем и т.п. Здесь студентам дается право самостоятельно перестроить графическую модель, которая изначально была обозначена преподавателем на лекции, так, как это будет им понятно.

«Абстрактная модель» подачи информации заключается в непосредственном строгом абстрактном определении какого-либо математического понятия или теоремы, данной в учебнике.

Сравнивая эти три «модели», следует отметить их отличительные особенности: в алгоритмической модели идет постепенное развертывание математического понятия, то есть, не выполнив первый и последующие шаги, невозможно сделать заключение, дать ответ на поставленный вопрос задачи; перескакивание с одного шага на другой исключено. Сложность графической «модели» состоит в первоначальном понимании самой конструкции схемы, чертежа, рисунка и т.д. и в невозможности самостоятельно определить порядок действий. Стоит отметить, что «графическая модель» требует от студента и преподавателя творческого подхода, поскольку для графического изображения необходимо включать воображение для создания «образов», применять умения и владеть навыками конструирования и рисования.

Самой трудной для понимания из этих трех «моделей» является абстрактная, так как: 1) она является основой построения двух первых моделей; 2) на ней строится вся фундаментальная наука математика.

Для эффективного усвоения материала необходимо эти «модели» реализовывать в единой системе. Подтверждением тому является точка зрения ученых Вакульчика В.С и Мателенка А.П., которые отмечают, что в основу когнитивно-визуального подхода в обучении положен принцип формирования образовательной технологии на основе взаимосвязи и единства абстрактно-логического содержания материала и методов с наглядно-интуитивными [6, c. 84].

Одна общая черта первых двух моделей – это четкое понимание смысла промежуточных действий, выполнение которых приведет к положительному результату решения поставленной задачи.

Итак, продемонстрируем каждую «модель» на примере изучения темы «Достаточные признаки сходимости положительных числовых рядов». В качестве примера рассмотрим признак сравнения.

Для студентов с развитым словесно-логическим мышлением предлагается алгоритм исследования на сходимость положительных числовых рядов при помощи признака сравнения.

Пусть требуется исследовать на сходимость положительный числовой ряд 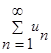, 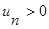(1). Составим следующий алгоритм:

1) за ряд сравнения 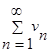, 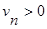(2) выбрать ряд, сходимость которого легко определить по сравнению с заданным рядом (1). Им может являться ряд с членами геометрической прогрессии; обобщенный гармонический ряд;

2) сравнить соответствующие члены ряда (1) и (2) и сделать вывод о сходимости ряда (1);

а) если ряд (2) сходится и 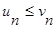, начиная с некоторого 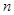, то ряд (1) также сходится;

б) если ряд (2) расходится и 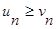, начиная с некоторого 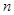, то ряд (1) также расходится;

3) если в а) и б) неравенство не выполняется, то следует выбрать другой ряд сравнения (2).

Данный алгоритм можно представить в виде блок-схемы (рис. 5), которая будет эффективна для усвоения данного признака студентами с преобладающим наглядно-образным мышлением.

Поэтому для успешного усвоения признака сравнения в теории числовых рядов необходимо знать саму теорему признака сравнения. Следует отметить, что независимо от того, какое мышление преобладает у студента, необходимо знать сами определения математических понятий, которыми легко владеют те, у кого развито абстрактно-символическое мышление.

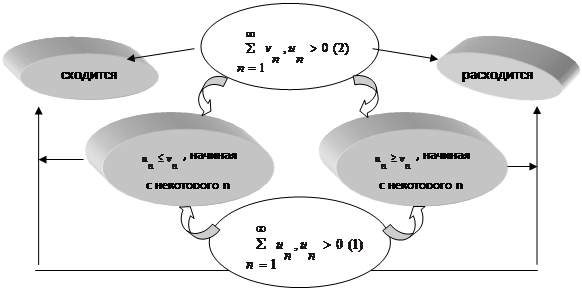
Рис. 5. Исследование на сходимость числового ряда при помощи признака сравнения

Например, при изучении темы «Знакочередующиеся ряды» студентам биологических направлений «Агрономия» и «Агрохимия и агропочвоведение», у которых преобладает словесно-логический тип мышления, целесообразно предложить следующий развернутый алгоритм исследования знакочередующихся рядов (ЗЧР) на абсолютную/условную сходимость.

Алгоритм:

1) построить ряд из абсолютных величин:

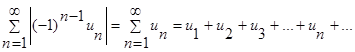(1)

2) проверить выполнимость условий признака Лейбница. Для этого:

а) сравнить члены положительного ряда (1), т.е. проверить выполнимость условия 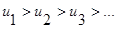, начиная с некоторого номера 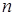(монотонное убывание членов ряда (1)). Если да, то перейти к б);

если нет, то ЗЧР расходится;

б) если предел 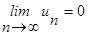, то ЗЧР сходится; если 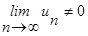, то ЗЧР расходится;

3) исследовать на сходимость ряд (1);

4) вывод:

а) если ряд (1) сходится, то ЗЧР сходится абсолютно;

б) если ряд (1) расходится, то ЗЧР сходится условно.

Большая часть респондентов, 52 человека (80%), считают именно эту модель наиболее понятной при выполнении типовых математических заданий, 10 (15,4%) из них выбрали графическую и лишь 3 человека (4,6%) – абстрактную (рис. 6). Первая модель легко воспринимается даже иностранными студентами. Однако у нее есть недостаток: трудна в применении решений нетиповых, нестандартных задач. Выбор третьей модели в малом количестве респондентами легко объясним тем, что среди 65 из них высоким уровнем такого типа мыслительной деятельности, как абстрактно-символический, обладают всего лишь 7 человек (11%) (табл. 1). Существует мнение, что людям с гуманитарным типом мышления недоступны точные науки, они слишком сложны, скучны и, как следствие, непонятны [7, с. 144]. Однако для повышения математической грамотности студентов, успешного овладения знаниями математики и дальнейшего применения их в профессиональной деятельности важны эффективные цели, задачи, методы и принципы обучения.

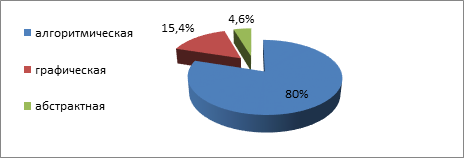
Рис. 6. Сравнение выбора «моделей» 65 респондентами

Этот же алгоритм, представленный графически в виде блок-схемы, будет полезен студентам с преобладанием наглядно-образного мышления (рис. 7).

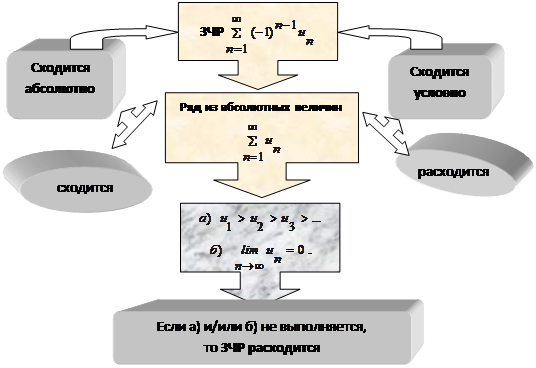
Рис. 7. Исследование ЗЧР на абсолютную/условную сходимость

Как отмечено в [8, с. 42]: «Предлагаемые схемы служат компактным описанием определенного отрезка учебного материала, помогают студенту с формированием и развитием представлений о структуре и взаимосвязях изучаемых математических объектов, требуют применения комплексных знаний и умений по изучаемой теме. В конечном итоге они дают наглядное представление о системе учебного материала, являются специальным и эффективным методическим средством, целенаправленно оказывающим усиливающее влияние на степень и уровень познавательной активности студентов».

Другое представление графической «модели» – в виде таблицы (табл. 3), которая будет полезна тому, у кого развито наглядно-образное мышление.

Таблица 3

Определение абсолютной/условной сходимости ЗЧР

Заключение. Одним из критериев оценивания профессионального мастерства преподавателя является уровень обученности студентов. Обучение математике студентов в вузе с учетом их индивидуальных психологических особенностей – сложная педагогическая задача, поскольку требует от преподавателя владения профессиональными компетенциями. Данная методология предполагает определение типов мышления у студентов уже на первом этапе изучения дисциплины «Математика». Далее необходимо перестроить весь лекционный и дидактический материал дисциплины в соответствии с тремя «моделями»: алгоритмической, графической, абстрактной. Для успешного математического обучения студентов необходимо данные модели рассматривать в единой системе, так как, во-первых, они имеют взаимную связь, во-вторых, в такой подаче они могут способствовать раскрытию творческого потенциала обучающихся, развитию критического ума, логического мышления, аналитических способностей. Практическая значимость этих «моделей» заключается в применении принципов построения данных моделей в любой другой предметной области.