При проектировании рабочих программ учебных предметов, курсов, дисциплин (модулей) в вузе предусматриваются соответствующие образовательные технологии, которые позволяют наиболее эффективным образом обеспечить достижение планируемых результатов обучения.
Как отмечает Л.С. Капкаева [1], национальный проект «Образование» нацеливает преподавателей на повышение качества образования и обновление его содержания.
Интенсификация учебного процесса и новые требования к нему вынуждают преподавателей изыскивать пути повышения качества обучения студентов в вузах. При этом можно как использовать новые формы организации и контроля аудиторной и самостоятельной работы студентов, так и совершенствовать уже имеющиеся традиционные.
Все студенты в течение всего периода обучения имеют дело с чертежами, схемами, расчетами, индивидуальными заданиями, курсовыми проектами, при выполнении которых могут сделать ошибки. Поэтому преподавателям вузов необходимо заранее продумывать стратегию проведения работы над ошибками, которая должна включать в себя изучение существующего положения дел, оценку слабых и сильных сторон обучающихся, что позволит определить порядок и систему проведения работы над ошибками, регулярно оценивать эффективность данных мероприятий и принимать корректирующие и предупреждающие меры.
Все ошибки можно разделить на типичные и однократные. Типичные ошибки – это ошибки, которые повторяются у обучающегося неоднократно или у многих обучающихся однократно. Как правило, однократные ошибки встречаются единожды и носят нетипичный характер.
Современные педагогические исследования показывают, что работать над ошибками преподавателям необходимо совместно с обучающимися. Данный процесс очень полезен и актуален, поскольку позволяет студентам учиться на своих ошибках и не допускать их впредь. Работа над ошибками позволяет им осмысливать и понимать суть проблемы, понятия, правила и т.д.
Важно отметить, что такая работа должна носить систематический и целенаправленный характер в течение всего периода обучения, что позволит обучающему не делать ошибки или учиться самостоятельно их исправлять.
Организационные мероприятия, проводимые преподавателем, есть естественный результат нахождения ошибок, поскольку причины, вызывающие их, достаточно разнообразны, но в любом случае они направлены на уменьшение рисков и создание более благоприятных условий для обучающихся.
Исследования, связанные с выявлением и предупреждением типичных ошибок по математике у обучающихся, постоянно находят отклик у педагогов.
Отечественные ученые В.А. Далингер, Л.М. Бронникова, И.В. Кисельников, И.В. Ященко и иные проводили исследования в следующих направлениях:
– изучение типичных ошибок учащихся при решении логарифмических уравнений, неравенств и их систем [2];
– изучение типичных ошибок, которые совершали обучающиеся при решении геометрических задач [3];
– изучение типичных ошибок по математике, допускаемых школьниками на Едином государственном экзамене [4, 5];
– изучение типичных ошибок в конкретных задачах по математике для профильного уровня, т.е. ошибок, которые совершали учащиеся, планирующие обучаться в технических вузах [6].
Зарубежные педагоги рассматривали ошибки, связанные с непониманием студентами математической проблемы [7], с решением геометрических задач [8], с неправильным применением алгоритмов при решении примеров [9] и т.д.
Проведенный анализ исследований показал, что процесс отыскания и исправления ошибок очень полезен как для преподавателей, так и для обучающихся.
Стоит отметить, что имеется мало исследований, посвященных изучению и устранению ошибок, которые совершают иностранные граждане, обучаясь на подготовительном отделении на неродном языке.
Цель исследования – повышение качества обучения иностранных студентов на основе анализа типичных ошибок, совершаемых ими при выполнении заданий по математике.
Материал и методы исследования
Исследование проводилось на основе применения теоретических (анализ научно-методической литературы, в частности педагогических исследований, связанных с изучением у обучающихся типичных ошибок по математике) и эмпирических (исследование работ обучающихся на предмет выявления типичных ошибок по математике, тестирование студентов и опрос преподавателей математики) методов, а также методов статистики, применяемых в педагогических исследованиях.
Исследование осуществлялось на базе Томского политехнического университета (ТПУ) с иностранными студентами подготовительного отделения. В эксперименте, который был проведен в 2018–2019 учебном году, приняли участие 62 обучающихся.
До поступления на первый курс иностранные студенты подготовительного отделения ТПУ в течение года изучают базовые дисциплины на русском языке. Основная часть изучают дисциплины технического профиля, так как планируют продолжить свое дальнейшее обучение в ТПУ или в других технических вузах России.
По программе предвузовской подготовки технического профиля в ТПУ предусмотрено изучение таких дисциплин, как русский язык как иностранный, математика, физика, химия, инженерная графика и информатика.
Иностранным студентам предстоит выучить на русском языке основные термины, понятия и символику по математике и другим дисциплинам. Обучение на подготовительном отделении помогает студенту не только освоить терминологию по дисциплинам предвузовской подготовки, но и еще раз повторить основные разделы школьных курсов различных дисциплин.
Результаты исследования и их обсуждение
Чтобы обучение иностранных студентов на подготовительном отделении было эффективно, необходимо начать с выявления проблем, которые возникают у них в процессе обучения. К таким проблемам относятся:
– низкий уровень владения русским языком для повторения изучаемого теоретического материала;
– низкий уровень школьной подготовки;
– трудности в освоении специальной терминологии [10].
Решение вышеуказанных проблем непосредственно связано с изучением и анализом типичных ошибок, которые допускают иностранные граждане при обучении на подготовительном отделении.
В нашей работе проведено исследование, направленное на выявление типичных ошибок, которые допускали студенты из Монголии, Китая, Вьетнама и Индонезии при изучении математики на русском языке. На основе анализа работ студентов нами были выделены основные четыре группы ошибок.
К первой группе типичных ошибок отнесены вычислительные ошибки (действия с обыкновенными, смешанными и десятичными дробями) и ошибки, связанные c преобразованиями алгебраических выражений и дробей (неправильное раскрытие скобок, сокращение дробей, вынесение общего множителя за скобки и т.д.).
Например, применение формулы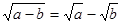 
обязательно происходит независимо от того, повторяются ли со студентами на занятии свойства радикалов или нет. Студенты проводят аналогию с формулой 
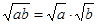, где а ≥ 0, b ≥ 0, и не понимают, почему они ошиблись. Если предложить студентам выучить свойства корней, то долговременного эффекта не получится. Необходимо, чтобы они поняли и осознали, почему совершили ошибку. В этом случае обучающемуся можно предложить вычислить 
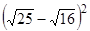по тому алгоритму, который он применил. В результате он получит 
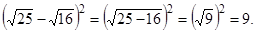Одновременно ему можно показать, что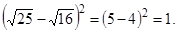 
Рассмотрим пример типичной ошибки, которую совершают студенты при сокращении алгебраических дробей. Например, в задании было предложено сократить следующую дробь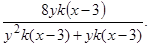 
Приведем неправильные ответы: 1)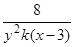 
; 2) 
.
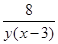Проведем анализ решений. В первом случае студенты сократили числитель дроби и второе слагаемое, стоящее в знаменатели дроби. Таким образом, они не учли, что в знаменателе дроби стоит знак «плюс», а не знак «умножить».
Приведем решение задания, которое привело ко второму ответу:
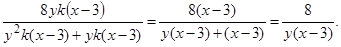
Изучив решение студента, можно увидеть, что сначала он сократил числитель и первое слагаемое, стоящее в знаменателе дроби, а потом сократил числитель и второе слагаемое, стоящее в знаменателе дроби. В этом случае преподаватель должен предложить обучающимся умножить числитель и знаменатель полученной ими дроби на выражение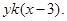 
Ко второй группе типичных ошибок отнесены ошибки решения уравнений и неравенств (ошибки, связанные с тождественными преобразованиями, с потерей корней уравнений, с нахождением области допустимых значений и т.д.).
Например, решая неравенство х2 ≤ 16, студенты часто записывают результат: х ≤ ±4. В этом случае обучающемуся можно предложить подставить вместо х значение 5 в исходное неравенство, чтобы он мог убедиться, что получится неверное неравенство: 25 ≤ 16.
Рассмотрим уравнение
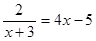. Решение данного уравнения сводится к следующему квадратному уравнению 
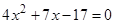, где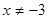
. Но часть студентов получили другое квадратное уравнение, например квадратное уравнение: 
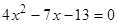. Отметим ошибки, которые сделали обучающиеся при решении уравнения: не учли область допустимых значений уравнения, не изменили знаки у слагаемых при переносе в другую часть уравнения, неправильно привели подобные слагаемые, допустили вычислительные ошибки при нахождении дискриминанта квадратного уравнения.
При решении уравнений вида
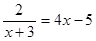преподавателям следует предложить студентам сделать проверку, подставив корни уравнения в первоначальное уравнение. Потом преподавателю необходимо последовательно объяснить студентам решение и предложить им решить несколько уравнений, используя предложенный алгоритм.
К третьей группе типичных ошибок были отнесены ошибки, связанные с основными понятиями функций (область определения функции, четные и нечетные функции, периодические функции, график функции и т.д.).
Встречаются студенты, которые не умеют строить такие простые графики функций, как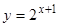 
, 
, 
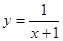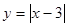и т.д. Для того чтобы построить графики функций, обучающиеся составляют таблицу из значений х и соответствующих им значений у. Отметив точки на координатной плоскости и соединив их, студенты получают прямую или ломаную линию.
Следует отметить, что часть студентов не могут выполнить задания, связанные с построением элементарных графиков функций. Поэтому преподавателям необходимо отработать с обучающимися построение таких графиков.
К четвертой группе типичных ошибок отнесены ошибки, допускаемые иностранными студентами при решении геометрических задач (непонимание смысла теорем в геометрии и незнание свойств фигур; неправильные геометрические построения по условию задачи).
Существенные пробелы в геометрической подготовке сохраняются у значительной доли иностранных студентов подготовительного отделения. Преподавателю следует обратить особое внимание на изучение основных фигур на плоскости и их элементов на русском языке, входящих в формулировки геометрических задач, на понимание условия задачи и правильное построение чертежа к нему. Конечно, часть ошибок иностранные студенты совершают при выполнении чертежей в силу того, что неверно понимают условие задачи на неродном языке. Поэтому преподавателю необходимо отрабатывать основные термины из геометрии на русском языке и сопровождать их геометрической иллюстрацией.
Для осуществления самоконтроля правильности проведенного решения задачи или примера, выполнения задания иностранным студентам предлагаются электронные курсы, представленные в среде Moodle и адаптированные для их восприятия. Любую тему по предмету обучающиеся имеют возможность повторять неоднократно, чтобы лучше понять условие и запомнить основные математические термины, а также улучшить свой результат. Если студенты неправильно выполнили задание в электронном курсе, то они получают к заданию комментарии от преподавателя, которые помогают им разобраться в сделанных ошибках.
Рассмотрим, как проводилось исследование на выявление типичных ошибок по математике у иностранных студентов подготовительного отделения ТПУ. На первом этапе исследования был проведен входной контроль по математике. Задания по данному предмету были составлены на основе базовых заданий, предлагаемых российским школьникам после окончания школы на Едином государственном экзамене. Так как иностранные студенты приехали обучаться на подготовительное отделение практически с нулевым знанием русского языка, то задания были переведены на родной язык обучающихся. Преподавателями математики был проведен анализ результатов входного контроля на предмет ошибок, которые сделали иностранные обучающиеся при выполнении заданий.
После годичного обучения на подготовительном отделении иностранные студенты прошли повторное тестирование. В задания контрольного среза (повторного тестирования) были включены задания, в которых иностранные обучающиеся допускали ошибки четырех типов.
Результаты входного и итогового контроля показали, что методика повторения школьного курса математики на русском языке с учетом типичных ошибок позволила повысить уровень знаний у иностранных студентов подготовительного отделения.
Количество обучающихся, которые допускали типичные ошибки, относящиеся к первой группе, к концу учебного года уменьшилось на 14,5%. Число студентов, которые совершили типичные ошибки, относящиеся ко второй группе, при итоговом тестировании снизилось на 16%. Количество студентов, которые сделали ошибки, относящиеся к третьей группе, уменьшилось в 2 раза.
Отметим, что число студентов, совершивших ошибки при решении геометрических задач (четвертая группа типичных ошибок), на момент входного и итогового контроля практически не изменилось. Это обусловлено тем, что геометрию изучают на русском языке в конце учебного года, причем на нее отводится незначительное количество часов, тогда как тождественными преобразованиями, вычислениями, построением графиков элементарных функций иностранные студенты занимаются в течение всего учебного года.
Заключение
Таким образом, качество обучения напрямую зависит от анализа ошибок, которые делают иностранные студенты при поступлении в высшие учебные заведения. Кроме того, систематизация работ обучающихся, в которых встречаются ошибки, требует целенаправленной и методической деятельности преподавателя. При этом необходимо объединять ошибки по группам, чтобы в дальнейшем работать над методикой их устранения. Проводя такую работу, преподаватель сможет предупредить появление ошибок у обучающихся и наметить пути их исправления. Отметим, что от того, насколько успешно иностранный студент пройдет годичный курс предвузовской подготовки, будет зависеть его дальнейшее обучение в российских вузах на неродном языке.