В связи с переходом на двухуровневую систему [1] образования значительно возросло количество часов в учебном плане, отводимых на самостоятельную работу студента. Для ее эффективной организации широко применяются дистанционные технологии. Помимо того что указанные технологии являются хорошим инструментом организации познавательной самостоятельности студента [2], существует и ряд других плюсов их применения. Рассмотрим некоторые из них.
1. Возможность обучаться в удобное время. Действительно, обучаясь дистанционно, студент имеет возможность построить свой индивидуальный график обучения, может сам определять, когда и сколько времени потратить на изучение того или иного материала.
2. Возможность готовиться в своем темпе. При традиционной форме обучения преподаватель, как правило, ориентируется на определенную группу студентов-«середняков». При дистанционном способе обучение проходит в темпе, удобном для студента. Он всегда может вернуться к изучению более сложных тем, повторно пройти лекционный материал, задать вопросы преподавателю в режиме онлайн.
3. Возможность получать знания в удобном месте. При дистанционной форме обучения студент может обучаться, не выходя из дома, что особенно актуально для людей с ограниченными возможностями здоровья, для людей с маленькими детьми. Это также актуально в период действия карантинных мер.
4. Возможность обучаться, не прерывая трудовой деятельности.
5. Доступность учебных материалов. При дистанционной форме обучения весь учебно-методический материал, как правило, выложен на курсе.
6. Возможность реализации индивидуального подхода. При традиционной форме обучения преподавателю довольно сложно уделить внимание каждому студенту, подстроиться под темп каждого из них. В случае же дистанционного обучения обучающийся имеет возможность получать ответы на свои вопросы в удобном для него режиме.
7. Удобство для преподавателя. При дистанционном обучении преподаватель имеет возможность наблюдать за процессом обучения, даже находясь в командировке.
Однако существует и ряд минусов такой формы обучения [3].
1. Необходимость наличия у учеников сильной мотивации. Так как при дистанционной форме обучения студент весь материал изучает самостоятельно, это требует от него хорошей силы воли, самодисциплины, усидчивости и ответственности.
2. Уклон в сторону теоретических знаний. Действительно, при дистанционной форме довольно сложно осуществить изучение дисциплин, требующих большого количества практических занятий.
3. Проблема контроля процесса обучения. К сожалению, в большинстве случаев при дистанционном обучении невозможно проверить, насколько честно студент относится к выполнению заданий, сам ли выполняет их.
4. Невозможность развития таких личностных качеств, как коммуникабельность, умение работать в команде, ораторские качества.
Цель исследования: показать на примере дистанционного курса «Математика и основы математической обработки информации», созданного на базе системы LMS МOODLE, один из вариантов формирования познавательной самостоятельности студента, позволяющий максимально эффективно организовать самостоятельную работу студентов и минимизировать минусы от применения дистанционных технологий. На основе статистических данных, собранных в процессе работы студентов над указанным курсом, провести оценку эффективности применения дистанционных технологий в вузе при изучении математики.
Материал и методы исследования. Покажем на примере дистанционного курса «Математика и основы математической обработки информации», созданного на базе системы LMS МOODLE, один из вариантов формирования познавательной самостоятельности студента, позволяющий максимально эффективно организовать самостоятельную работу студентов и минимизировать минусы от применения дистанционных технологий. Сначала опишем структуру курса, схему работы с ним, а затем изложим суть педагогического эксперимента, проведенного автором статьи для оценки эффективности использования дистанционных технологий при изучении математики.
Рассматриваемый курс состоит из следующих тем (разделов).
1. Основные средства представления информации в математике и их использование в педагогической деятельности.
2. Элементы теории множеств. Графы. Функции.
3. Элементы теории вероятностей.
4. Элементы математической статистики.
Каждый раздел включает в себя конспект лекций с примерами решения типовых заданий и вопросами для самопроверки. После изучения лекционного материала студент переходит к вопросам. При возникновении сложностей с ответами на них обучающийся может вернуться к изучению той части лекционного материала, которая вызвала трудности. Далее студент переходит к тестированию, результаты которого демонстрируют степень освоения им данного материала и возможность перехода к изучению нового раздела. Тестирование также можно пройти повторно, если первоначальный результат не соответствует требованиям, устанавливаемым преподавателем (преподавателю эти попытки видны из его личного кабинета). Итоговой формой контроля для каждого раздела является проверочная работа. Выполненные проверочные работы присылаются преподавателю для оценивания. На основании указанных форм контроля выставляется оценка.
После изучения всех разделов необходимо пройти итоговое тестирование, вопросы (задания) которого охватывают весь лекционный и практический материал по курсу.
Каждое лекционное и практическое занятие сопровождается методическими указаниями и списком литературы, который может быть полезен при возникновении вопросов в процессе изучения материала. Студент также может задать вопрос по курсу непосредственно преподавателю с помощью интерактивных форм общения, интегрированных в систему LMS МOODLE, а основные определения и термины, встречающиеся в процессе изучения дисциплины, обучающийся может найти в глоссарии.
Как отмечалось выше, одним из минусов дистанционного обучения является тот факт, что невозможно в полной мере оценить, насколько честно тот или иной студент подходит к выполнению заданий, нельзя проверить, самостоятельно ли он выполнял предлагаемые задания. Поэтому завершается курс итоговой проверочной работой, которая проводится в аудитории и включает в себя задания из каждой темы курса. Приведем один из вариантов этой проверочной работы [4, 5].
1. Экзамен по русскому языку сдавали 240 абитуриентов, из них 170 человек получили оценку ниже 5 баллов, 205 человек сдали этот экзамен, т.е. получили оценки 3, 4 или 5. Сколько человек получили оценки 3 и 4?
2. Из 37 студентов филологического факультета оценку «отлично» по русскому языку получили 15 студентов, по литературе – 14, по языкознанию – 18, по русскому языку и литературе – 6, по русскому языку и языкознанию – 9, по литературе языкознанию – 5, по всем трем дисциплинам – 4. Сколько студентов получили хотя бы по одной оценке «отлично»?
3. В соревнованиях по бадминтону участвуют 10 спортсменов. Соревнования проходят по олимпийской системе, при которой участник выбывает из турнира после первого же проигрыша. За какое минимальное количество часов можно провести соревнования, если в распоряжении оргкомитета 2 корта и на каждую встречу, включая разминку и отдых, отводится час?
4. На экзамен необходимо было подготовить 30 билетов. Студент подготовил только 25 из них. Он извлекает поочередно два билета. Найти вероятность того, что он сдаст экзамен, если для этого нужно ответить хотя бы на один билет, а в первый раз был вынут невыученный билет?
5. Была проведена одна и та же проверочная работа в двух группах. В первой группе из 25 студентов 8 выполнили работу на «отлично», во второй, состоящей из 30 студентов, – 6 «отличных» работ. Какова вероятность того, что выбранная наудачу работа из наудачу выбранной группы окажется «отличной»?
6. Пусть задана совокупность значений признака: 15; 20; 18; 20; 25; 11; 12; 13; 24; 23; 23; 24; 21; 22; 21; 23; 23; 22; 21; 14; 14; 22; 15; 16; 20; 20; 16; 16; 20; 17; 17; 17. Нужно составить вариационный и статистический ряды распределения, вычислить числовые характеристики.
7. Отобраны 5 студентов для участия в олимпиаде по программированию. Компьютерная программа фиксирует (табл. 1) время решения каждого задания (всего три задания). Необходимо определить, существуют ли статистически значимые различия между временем решения задач?
Таблица 1
Время решения задания
|
№ испытуемых (п/п). |
Время решения первого задания (мин) |
Время решения второго задания (мин) |
Время решения третьего задания (мин) |
|
1 |
24 |
18 |
22 |
|
2 |
16 |
14 |
15 |
|
3 |
12 |
10 |
16 |
|
4 |
5 |
4 |
12 |
|
5 |
6 |
16 |
8 |
8. Отобраны 15 студентов первого курса. Им задан вопрос: «Сколько времени вы потратили на подготовку к зачету?» Их ответы (в часах): 8, 6, 3, 1, 0, 5, 9, 2, 1, 4, 6, 10, 0, 3, 6. Необходимо найти коэффициент вариации и сделать соответствующий вывод.
Теперь опишем проведенный автором педагогический эксперимент, позволяющий оценить эффективность использования дистанционных технологий при изучении математики в образовательной деятельности вуза. Для этого в начале 1-го семестра (2019–2020 уч. год) были отобраны две группы студентов, обучающихся по направлению 44.03.05 Педагогическое образование (с двумя профилями подготовки). Профиль подготовки группы № 1 – Русский язык и литература (дистанционное обучение), группы № 2 – История и обществознание (традиционное обучение). В каждой из групп были отобраны по 5 студентов со следующими баллами по ЕГЭ по математике (базовый уровень): первая группа – 61, 62, 65, 59, 58, вторая группа – 60, 60, 64, 58, 64.
Сначала выясним, целесообразно ли проводить эксперимент среди этих студентов. Для этого вычислим выборочную среднюю:
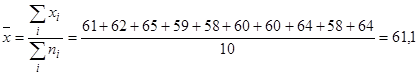 .
.
Далее найдем ошибку репрезентативности выборочной средней:
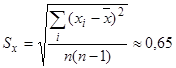 .
.
Наконец, найдем коэффициент вариации:
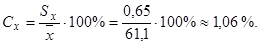
Так как коэффициент вариации меньше 5%, следовательно, в нашем случае участники групп несущественно отличаются друг от друга по количеству баллов ЕГЭ по математике, значит, исследование проводить можно.
В группе № 1 занятия проводились в дистанционном формате с использованием описанного выше курса, а в группе № 2 – в аудитории.
В конце семестра после прохождения курса была проведена проверочная работа (в аудитории) в обеих группах (примерный вариант проверочной работы представлен выше). Результаты выполнения проверочной работы (в процентах) отобранных для исследования студентов таковы:
группа № 1: 72, 83, 78, 73, 72;
группа № 2: 76, 77, 88, 83, 79.
Оценим, насколько отличается эффективность выполнения проверочной работы (а, следовательно, и результат освоения дисциплины в целом) в зависимости от формы обучения. Найдем среднее значение (в процентах) и дисперсию в каждой группе.
Группа № 1:
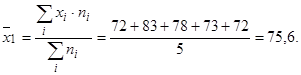
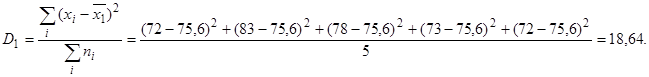
Группа № 2:
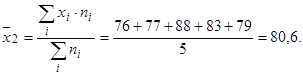
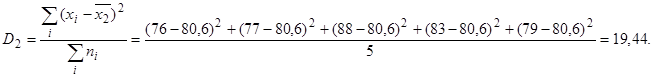
Запишем эти данные в табличной форме (табл. 2).
Таблица 2
Результаты выполнения проверочной работы
|
Группа |
Среднее значение, %. ( |
Численность группы, человек (ni) |
Дисперсия в группе (Di) |
|
№ 1 |
75,6 |
5 |
18,64 |
|
№ 2 |
80,6 |
5 |
19,44 |
Найдем среднее значение (в процентах) для всех студентов:
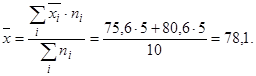
Вычислим внутригрупповую дисперсию:
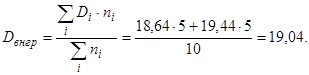
Найдем межгрупповую дисперсию:
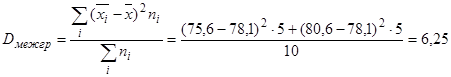 .
.
Используя два предыдущих значения, найдем общую дисперсию:
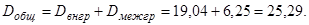
Наконец, вычислим коэффициент детерминации, который и характеризует, в какой степени успешность освоения материала зависит от выбора формы обучения:
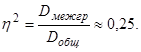
Результаты исследования. Полученный результат говорит о том, что успешность освоения материала на 25% выше в случае, если обучение проводится в традиционной форме.
Вывод. Таким образом, как показывают результаты проведенного эксперимента, при изучении математики студент лучше усваивает материал при традиционной форме обучения. Однако в случаях, когда присутствие студента в аудитории невозможно по каким-либо причинам (болезнь, семейные обстоятельства и пр.), дистанционные курсы, такие как, например, описанный здесь курс «Математика и основы математической обработки информации», позволяют организовать самостоятельную работу студентов, способствуют развитию способности к самообразованию.




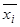 )
)