Шизофрения относится к типу психотических заболеваний, важным признаком которых является значимая потеря контактов с реальностью [1–3].
До настоящего момента были неизвестны подходы, устанавливающие связь данного заболевания с изменением параметров крови. В этой статье проведена апробация методики, позволяющей с высокой вероятностью констатировать наличие патологии у больного с установленным диагнозом наличия шизофрении на основе ИК-спектроскопического исследования крови. В сочетании с предварительно сформулированным врачом предположением о возможности заболевания шизофренией у вновь обследуемого пациента информация о наличии аналогичных признаков при обработке анализа крови может служить серьезным объективным подтверждением справедливости указанного диагноза.
В данной статье проводится обоснование методики определения статуса состояния здоровья пациента, предложенной в работе [4]. При кратком изложении подхода, изложенного в указанной работе, напомним, что в [4] биологические величины 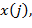
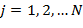 , измеряемые при обработке данных анализа с целью обнаружения заболевания у обследуемого пациента, рассматривались как сумма случайных слагаемых вида:
, измеряемые при обработке данных анализа с целью обнаружения заболевания у обследуемого пациента, рассматривались как сумма случайных слагаемых вида:
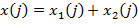 . (1)
. (1)
Здесь совокупность 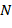 случайных величин (СВ)
случайных величин (СВ) 
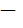 последовательность параметров, связанных с функционированием организма пациента. В правой части (1) ансамбли СВ
последовательность параметров, связанных с функционированием организма пациента. В правой части (1) ансамбли СВ 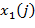 и
и 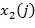 отвечают соответственно нормальной жизнедеятельности организма и влиянию заболевания (при отсутствии которого все
отвечают соответственно нормальной жизнедеятельности организма и влиянию заболевания (при отсутствии которого все 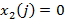 .)
.)
В [4] была выдвинута и подтверждена дальнейшими расчетами гипотеза о том, что 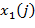 и
и 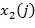 могут рассматриваться как два статистически взаимно независимых набора случайных величин. С медицинской точки зрения это объясняется тем, что нормальная жизнедеятельность организма должна быть слабо связано с «функционированием» заболевания (по крайней мере на ранних стадиях развития последнего). Поэтому в [4] был введен в рассмотрение математический оператор вида
могут рассматриваться как два статистически взаимно независимых набора случайных величин. С медицинской точки зрения это объясняется тем, что нормальная жизнедеятельность организма должна быть слабо связано с «функционированием» заболевания (по крайней мере на ранних стадиях развития последнего). Поэтому в [4] был введен в рассмотрение математический оператор вида

где 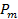 – вероятность попадания значений ансамбля СВ
– вероятность попадания значений ансамбля СВ 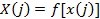 в интервал
в интервал
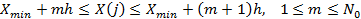 . (3)
. (3)
Здесь 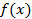 – произвольная функция, плотность вероятности которой при равномерном распределении значений аргумента обладает одной или несколькими интегрируемыми особенностями. Ее использование, как показано в [4], позволяет резко усилить (по сравнению с использованием в (3) ансамбля величин
– произвольная функция, плотность вероятности которой при равномерном распределении значений аргумента обладает одной или несколькими интегрируемыми особенностями. Ее использование, как показано в [4], позволяет резко усилить (по сравнению с использованием в (3) ансамбля величин 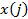 вместо
вместо 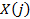 , см. (1)) эффективность применения оператора (2) по выявлению признаков группового отличия кривых вида
, см. (1)) эффективность применения оператора (2) по выявлению признаков группового отличия кривых вида 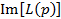 ,
,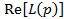 ,
, 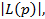
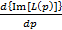 и иных для здорового организма пациента и при наличии болезни. Значение
и иных для здорового организма пациента и при наличии болезни. Значение 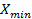 в (3) – в общем случае свое для каждого отдельного анализа. Далее, в порядке развития методики [4], будем полагать
в (3) – в общем случае свое для каждого отдельного анализа. Далее, в порядке развития методики [4], будем полагать
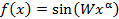 , (4)
, (4)
вследствие чего в (2) вместо 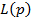 будем использовать обозначение
будем использовать обозначение 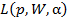 . Для всех реализаций случайной локальной последовательности значений
. Для всех реализаций случайной локальной последовательности значений 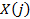 (каждая из которых отвечает одному анализу крови для одного пациента) в (3) удобно принять
(каждая из которых отвечает одному анализу крови для одного пациента) в (3) удобно принять
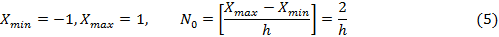
(в (5) квадратные скобки означают целую часть числа).
В (4) параметры 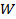 ,
, 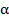 и интервал дискретизации
и интервал дискретизации 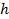 – свои для каждого отдельного заболевания, наличие которого, как показано ниже, с большой вероятностью может быть установлено при помощи оператора (2). В настоящей работе рассматриваемая методика используется с целью констатации характерных изменений свойств функционала (2), связанных с наличием шизофрении у соответствующей группы пациентов.
– свои для каждого отдельного заболевания, наличие которого, как показано ниже, с большой вероятностью может быть установлено при помощи оператора (2). В настоящей работе рассматриваемая методика используется с целью констатации характерных изменений свойств функционала (2), связанных с наличием шизофрении у соответствующей группы пациентов.
Цель исследования – выявление возникающих при шизофрении характерных изменений в свойствах статистических функционалов, вычисленных по совокупности ИК-спектроскопических параметров крови, отвечающей анализу крови для отдельно взятого пациента.
Материалы и методы исследования. Исследование проведено на базе клиник неврологии, психиатрии и наркологии ФДПО совместно с кафедрой общей химии ПИМУ. Методом инфракрасной спектроскопии сыворотки крови [5] проведен анализ у всех больных с клиническим диагнозом «шизофрения» (n=25) и здоровых добровольцев (n=32).
Исследование проведено в соответствии с Хельсинкской декларацией, принятой в июне 1964 г. (Хельсинки, Финляндия) и пересмотренной в октябре 2000 г. (Эдинбург, Шотландия), и одобрено Этическим комитетом ПИМУ. От каждого пациента получено информированное согласие.
За ИК-спектроскопические параметры принимали абсолютные и относительные значения ИК-спектров сыворотки крови в диапазоне длин волн 1200–1000 см-1.
На основе полученных ИК-спектров крови рассчитаны значения статистических функционалов для каждого отдельного пациента [4].
Результаты исследования и их обсуждение. На рисунке 1а приведены зависимости 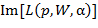 при
при 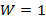 и
и 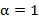 ; здесь и далее в (5) принято
; здесь и далее в (5) принято 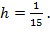 Зеленые кривые соответствуют анализам крови пациентов с нормальным состоянием здоровья, а красные и одна синяя линия отвечают аналогичным анализам для людей с установленной шизофренией. Каждая кривая соответствует одному анализу для одного человека и построена по 13 значениям отношений высот пиков полос поглощения (см-1/см-1):
Зеленые кривые соответствуют анализам крови пациентов с нормальным состоянием здоровья, а красные и одна синяя линия отвечают аналогичным анализам для людей с установленной шизофренией. Каждая кривая соответствует одному анализу для одного человека и построена по 13 значениям отношений высот пиков полос поглощения (см-1/см-1):
1 — 1165/1160, 2 — 1165/1070, 3 — 1165/1150, 4 — 1165/1140,
5 — 1040/1070, 6 — 1165/1130, 7 — 1070/1025, 8 — 1165/1050,
9 — 1165/1025, 10 — 1100/1050, 11 — 1170/1150, 12 — 1170/1160,
13 — 1125/1165.
На данном рисунке область, выделенная оранжевым прямоугольным контуром, содержит отрезки 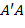 и
и 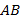 c координатами граничных точек
c координатами граничных точек 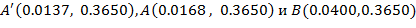 , что более подробно показано на рисунке 1б. Фиолетовый отрезок
, что более подробно показано на рисунке 1б. Фиолетовый отрезок 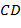 на рисунке 1а проходит между точками
на рисунке 1а проходит между точками 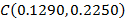 и
и 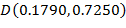 .
.
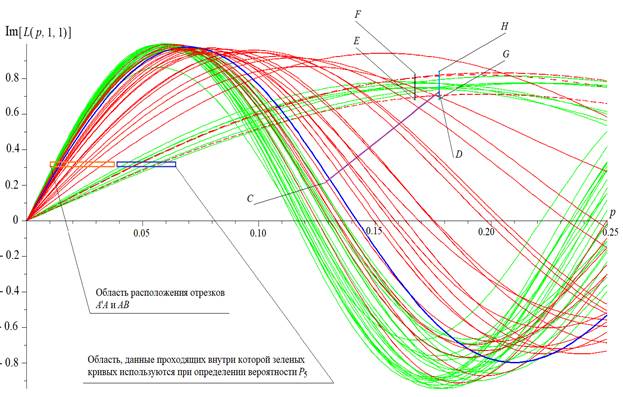
Рис. 1а. Сопоставление ансамблей зависимостей 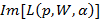 при
при 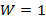 и
и 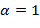 для здоровых пациентов (зеленые кривые) и при установленном диагнозе шизофрении (красные и одна синяя линии)
для здоровых пациентов (зеленые кривые) и при установленном диагнозе шизофрении (красные и одна синяя линии)
Как видно из рисунков 1а и 1б, отрезки 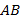 и
и  не имеют общих точек ни с одной из 32 зеленых линий, но пересекаются соответственно 17-ю и 16-ю из 25 красных кривых. С точки зрения авторов, любое такое пересечение является серьезным основанием для утверждения о наличии проблем со здоровьем у соответствующего пациента. Для получения вероятностной оценки достоверности данного вывода далее применяется неравенство Чебышева [6–8]. Пока же подчеркнем, что в обоих случаях речь идет не о случайных флуктуациях той или иной зависимости, а именно о групповом свойстве ансамблей красных и зеленых линий. (Указанное свойство, что очень важно, проявляется в области с подобной топологией обоих рассматриваемых ансамблей кривых.) Одновременно с этим указанные отрезки определяют направления прямых, вдоль которых проводится отсчет наборов случайных величин, связанных со взаимным расположением зеленых и красных кривых и использующихся при составлении оценок вероятностей на основе указанного неравенства.
не имеют общих точек ни с одной из 32 зеленых линий, но пересекаются соответственно 17-ю и 16-ю из 25 красных кривых. С точки зрения авторов, любое такое пересечение является серьезным основанием для утверждения о наличии проблем со здоровьем у соответствующего пациента. Для получения вероятностной оценки достоверности данного вывода далее применяется неравенство Чебышева [6–8]. Пока же подчеркнем, что в обоих случаях речь идет не о случайных флуктуациях той или иной зависимости, а именно о групповом свойстве ансамблей красных и зеленых линий. (Указанное свойство, что очень важно, проявляется в области с подобной топологией обоих рассматриваемых ансамблей кривых.) Одновременно с этим указанные отрезки определяют направления прямых, вдоль которых проводится отсчет наборов случайных величин, связанных со взаимным расположением зеленых и красных кривых и использующихся при составлении оценок вероятностей на основе указанного неравенства.
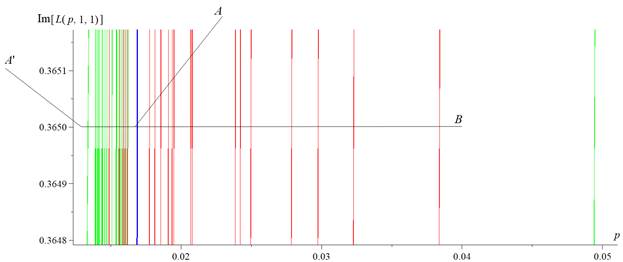
Рис. 1б. Подробный вид области, выделенной оранжевым
прямоугольным контуром на рисунке 1а
В то же время вертикальные отрезки {E(0.1686, 0.6850), F(0.1686, 0.8150)} и {G(0.1790, 0.6850), H(0.1790, 0.8330)} в верхней части рисунка 1а пресекаются как с зелеными, так и с красными кривыми. Математический смысл введения EF и GH состоит в том, что вдоль задаваемых ими направлений производится отчет параметров приведенных на рисунке 1а зависимостей; далее полученная последовательность случайных величин используется при проведении вычислений в соответствии с неравенством Чебышева.
В виде примера, поясняющего методику расчетов, рассмотрим отрезок EF. На рисунке 1в подробно показан вид участка рисунка 1а, расположенного вблизи EF. Здесь точки 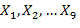 (при необходимости так же будем именовать изображенные на рисунке 1в кривые) соответствуют одному и тому же значению аргумента
(при необходимости так же будем именовать изображенные на рисунке 1в кривые) соответствуют одному и тому же значению аргумента 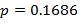 на оси абсцисс.
на оси абсцисс.
На рисунке 1в не приведены две наклонные сплошные красные кривые, которые на рисунке 1а проходят через данный участок декартовой плоскости 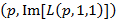 . Это связано с тем, что обе указанные линии пересекают отрезки
. Это связано с тем, что обе указанные линии пересекают отрезки 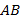 и
и 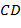 на рисунке 1а. Каждый факт такого пересечения, как будет показано далее, с большой долей уверенности может быть классифицирован как признак наличия патологии в состоянии здоровья соответствующего пациента. Кроме того, изображенная на рисунке 1в нижняя красная пунктирная линия
на рисунке 1а. Каждый факт такого пересечения, как будет показано далее, с большой долей уверенности может быть классифицирован как признак наличия патологии в состоянии здоровья соответствующего пациента. Кроме того, изображенная на рисунке 1в нижняя красная пунктирная линия 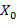 не участвует в дальнейших вычислениях, относящихся к рассматриваемому рисунку. (Для этой линии расчеты будут проведены отдельно; она приведена на рисунке 1в с целью подчеркнуть ее принадлежность к группе из трех красных кривых, которые в верхней части рисунка 1а проходят очень близко к локальному «потоку» из семи зеленых линий, подробно изображенному на рис. 1в.)
не участвует в дальнейших вычислениях, относящихся к рассматриваемому рисунку. (Для этой линии расчеты будут проведены отдельно; она приведена на рисунке 1в с целью подчеркнуть ее принадлежность к группе из трех красных кривых, которые в верхней части рисунка 1а проходят очень близко к локальному «потоку» из семи зеленых линий, подробно изображенному на рис. 1в.)
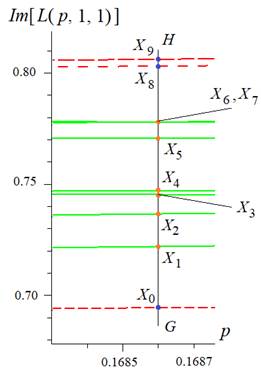
Рис. 1в. Подробный вид области вблизи отрезка EF на рисунке 1а
Целью дальнейших вычислений, связанных с рисунком 1в, является определение границы сверху для вероятности того, что две верхние линии на этом рисунке, отмеченные точками 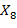 и
и 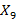 , не входят в семейство кривых
, не входят в семейство кривых 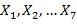 , что равносильно признаку наличия заболевания у соответствующих пациентов. (Обе кривые
, что равносильно признаку наличия заболевания у соответствующих пациентов. (Обе кривые 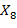 и
и 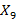 показаны красным пунктиром на рисунке 1а, где проходят выше уровня
показаны красным пунктиром на рисунке 1а, где проходят выше уровня 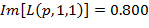 при рассматриваемых на рисунке 1в значениях горизонтальной переменной
при рассматриваемых на рисунке 1в значениях горизонтальной переменной  )
)
В соответствии с неравенством Чебышева полагаем, что для вероятности 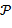 , характеризующей свойства приведенных на рисунке 1в зависимостей (математический смысл величины
, характеризующей свойства приведенных на рисунке 1в зависимостей (математический смысл величины 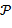 будет пояснен ниже), при
будет пояснен ниже), при 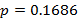 имеет место соотношение
имеет место соотношение

Здесь случайная величина 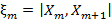 (где
(где 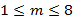 ) – расстояние между соседними точками
) – расстояние между соседними точками 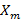 и
и 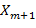 применительно к рисунку 1в. В (6) величины
применительно к рисунку 1в. В (6) величины 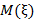 и
и 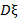 есть среднее значение и соответственно дисперсия данной СВ, определенные по первым 7 точкам
есть среднее значение и соответственно дисперсия данной СВ, определенные по первым 7 точкам 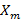 (отвечающим исключительно зеленым линиям). Им соответствуют 6 длин отрезков
(отвечающим исключительно зеленым линиям). Им соответствуют 6 длин отрезков 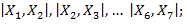 как видно из рисунка 1в,
как видно из рисунка 1в, 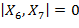 . Полагая здесь и далее величину доверительной вероятности равной
. Полагая здесь и далее величину доверительной вероятности равной 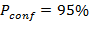 , для параметров рисунка 1в получаем оценку верхней границы доверительного интервала при расчете отвечающего зеленым кривым значения дисперсии
, для параметров рисунка 1в получаем оценку верхней границы доверительного интервала при расчете отвечающего зеленым кривым значения дисперсии 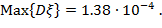
Аргумент 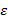 в левой половине неравенства (6) задает модуль
в левой половине неравенства (6) задает модуль
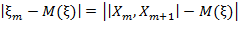 отклонения расстояния
отклонения расстояния 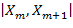 от
от 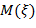 для произвольной пары последовательных кривых, изображенных на рисунке 1в. Поэтому правая часть (6) может рассматриваться как оценка сверху для вероятности
для произвольной пары последовательных кривых, изображенных на рисунке 1в. Поэтому правая часть (6) может рассматриваться как оценка сверху для вероятности 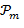 следующего события: значение
следующего события: значение 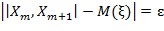 , и одновременно проходящая через точку
, и одновременно проходящая через точку 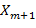 прямая относится к зеленому ансамблю линий, соответствующему нормальному состоянию здоровья обследуемого пациента. Согласно рисунку 1в для точек
прямая относится к зеленому ансамблю линий, соответствующему нормальному состоянию здоровья обследуемого пациента. Согласно рисунку 1в для точек 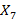 и
и 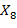 значение
значение 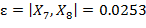 . Подставляя данную величину в (6) вместе с приведенной выше оценкой для дисперсии
. Подставляя данную величину в (6) вместе с приведенной выше оценкой для дисперсии 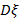 , получаем
, получаем

Согласно (6) соотношение (7) означает, что на рисунке 1в красная пунктирная линия, содержащая точку 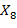 , может быть отнесена к группе кривых, соответствующих нормальному состоянию здоровья, с вероятностью не более
, может быть отнесена к группе кривых, соответствующих нормальному состоянию здоровья, с вероятностью не более 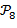 . Таким образом, минимальная вероятность патологии, которую обозначим в данном случае как
. Таким образом, минимальная вероятность патологии, которую обозначим в данном случае как 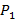 , для отвечающего данной кривой анализа крови составляет
, для отвечающего данной кривой анализа крови составляет

Очевидно, что вероятность 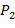 того, что красная кривая
того, что красная кривая 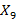 на рисунке 1в отвечает патологии, удовлетворяет неравенству
на рисунке 1в отвечает патологии, удовлетворяет неравенству 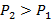 (поскольку, как видно из
(поскольку, как видно из 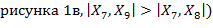 .
.
Для нижней красной пунктирной кривой на рисунке 1в вероятность патологии 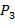 вычисляем по аналогии с
вычисляем по аналогии с 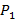 . В данном случае вертикальный отрезок GH, подобный EF, строится при
. В данном случае вертикальный отрезок GH, подобный EF, строится при 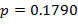 (при этом обращается в максимум входящее в (6) расстояние
(при этом обращается в максимум входящее в (6) расстояние 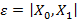 ). В итоге получаем, что минимальное значение
). В итоге получаем, что минимальное значение

Таким образом, на основе анализа рисунков 1а и 1в приходим к выводу, что в случае прохождения кривой 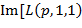 при
при 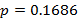 в области
в области 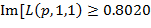 или при
или при 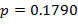 в интервале значений
в интервале значений 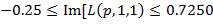 минимально возможная вероятность патологии определяется как
минимально возможная вероятность патологии определяется как 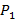 и соответственно
и соответственно 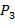 (см. (8) и (9)).
(см. (8) и (9)).
Как было отмечено выше, на рисунке 1б подробно показан участок, соответствующий области вблизи отрезка 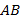 на рисунке 1а. В данном случае расчеты минимальной вероятности заболевания осуществляются (по аналогии с проведенными выше применительно к рисунку 1в) по совокупности расстояний
на рисунке 1а. В данном случае расчеты минимальной вероятности заболевания осуществляются (по аналогии с проведенными выше применительно к рисунку 1в) по совокупности расстояний 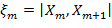 , отвечающих точкам пересечений продолжения
, отвечающих точкам пересечений продолжения 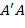 отрезка
отрезка 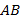 влево (см. рис. 1б), c группой «зеленых» графиков, расположенных левее точки
влево (см. рис. 1б), c группой «зеленых» графиков, расположенных левее точки 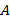 при
при 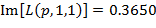 . Кроме того, учитывается точка пересечения отрезка
. Кроме того, учитывается точка пересечения отрезка 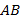 с изображенной на рисунках 1а и 1в синей линией. Последняя является наиболее близким к отрезку
с изображенной на рисунках 1а и 1в синей линией. Последняя является наиболее близким к отрезку 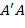 графиком (из числа расположенных вне
графиком (из числа расположенных вне 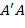 ), соответствующим установленному диагнозу рассматриваемого заболевания. Вновь применяя неравенство (6), получаем, что минимальная вероятность
), соответствующим установленному диагнозу рассматриваемого заболевания. Вновь применяя неравенство (6), получаем, что минимальная вероятность 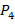 патологии для синей кривой составляет
патологии для синей кривой составляет

С математической точки зрения, правая часть (10) дает минимальную вероятность того, что синяя кривая не принадлежит к семейству «зеленых» зависимостей, расположенных левее точки 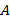 . Для всех красных линий, пересекающих отрезок
. Для всех красных линий, пересекающих отрезок 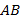 и расположенных правее синей кривой, вероятность указанной «непринадлежности» еще выше. При этом наличие внутри указанной группы зеленых кривых пяти красных линий, отвечающих установленному диагнозу рассматриваемой патологии у соответствующих пациентов, не влияет на подобный вывод, поскольку он связан с фактом значительно более разреженного прохождения красных графиков, пересекающих отрезок
и расположенных правее синей кривой, вероятность указанной «непринадлежности» еще выше. При этом наличие внутри указанной группы зеленых кривых пяти красных линий, отвечающих установленному диагнозу рассматриваемой патологии у соответствующих пациентов, не влияет на подобный вывод, поскольку он связан с фактом значительно более разреженного прохождения красных графиков, пересекающих отрезок 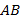 , по сравнению с зелеными кривыми, проходящими через
, по сравнению с зелеными кривыми, проходящими через 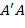 .
.
Проводя аналогичные расчеты с использованием семи зеленых линий, проходящих сквозь область, отмеченную синим прямоугольником на рисунке 1а (при проведении расчетов, как и ранее, по точкам пересечения соответствующих кривых с прямой 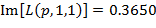 ), приходим к выводу, что в данном случае для линий, пересекающих отрезок
), приходим к выводу, что в данном случае для линий, пересекающих отрезок 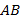 , вероятность патологии является величиной, не меньшей значения
, вероятность патологии является величиной, не меньшей значения

Результаты (10) и (11) практически совпадают.
Также проводя вычисления по аналогии, получаем, что для изображенного на рисунке 1а отрезка 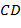 с определенными выше координатами граничных точек
с определенными выше координатами граничных точек 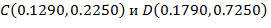 при пересечении его кривыми
при пересечении его кривыми 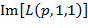 минимально возможное значение вероятности патологии составляет
минимально возможное значение вероятности патологии составляет

Вероятность (12), хотя и весьма велика, но все же меньше, чем (10) и (11). Тем не менее сам факт прохождения графика зависимости 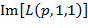 , кроме отрезка
, кроме отрезка 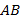 , также и через отрезок
, также и через отрезок 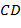 является дополнительным подтверждением правильности применяемой методики. Существенным представляется также тот факт, что для 17 «красных кривых», проходящих через отрезок
является дополнительным подтверждением правильности применяемой методики. Существенным представляется также тот факт, что для 17 «красных кривых», проходящих через отрезок 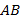 , вероятность патологии близка к значению вероятности заболевания, вычисляемой «по методу здравого смысла» в виде
, вероятность патологии близка к значению вероятности заболевания, вычисляемой «по методу здравого смысла» в виде

В (13) учтено, что сам факт прохождения зависимости 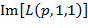 в той части интервала
в той части интервала 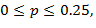 где топология всех линий взаимно подобна (см. рис. 1а), вне области 32 зеленых линий означает вероятность нормального состояния здоровья порядка
где топология всех линий взаимно подобна (см. рис. 1а), вне области 32 зеленых линий означает вероятность нормального состояния здоровья порядка 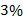 .
.
На рисунке 2а изображены оставшиеся 5 красных линий для тех приведенных на рисунке 1а зависимостей 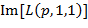 , что целиком «погружены» в массив зеленых кривых.
, что целиком «погружены» в массив зеленых кривых.
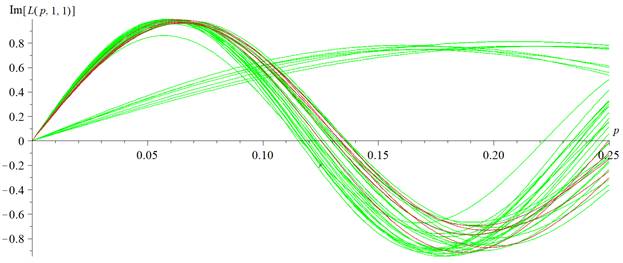
Рис. 2а. Сопоставление ансамбля зависимостей 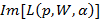 при
при 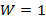 и
и 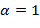 для здоровых пациентов (зеленые кривые) и пяти красных кривых, отвечающих установленному диагнозу шизофрении и целиком расположенных внутри массива зеленых линий
для здоровых пациентов (зеленые кривые) и пяти красных кривых, отвечающих установленному диагнозу шизофрении и целиком расположенных внутри массива зеленых линий
Строго говоря, для всех изображенных на этом рисунке пяти красных графиков, отвечающих установленным диагнозам о наличии шизофрении у обследуемых пациентов, на интервале 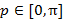 существует одна или несколько точек, в окрестности которых
существует одна или несколько точек, в окрестности которых 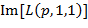 на небольшом участке оси абсцисс по абсолютной величине превышает значения модулей всех «зеленых» зависимостей. (Здесь учтено, что согласно (2) значения
на небольшом участке оси абсцисс по абсолютной величине превышает значения модулей всех «зеленых» зависимостей. (Здесь учтено, что согласно (2) значения 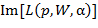 обладают периодом
обладают периодом 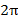 и относительно точки
и относительно точки 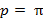 являются антисимметричными, то есть
являются антисимметричными, то есть 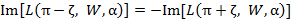 ; именно поэтому имеет смысл рассматривать только интервал
; именно поэтому имеет смысл рассматривать только интервал 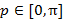 .) Но при этом координата
.) Но при этом координата 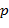 указанного превышения является своей для каждого красного графика. Это означает слабую достоверность маркера такого рода, поскольку может быть обусловлено случайными флуктуациями не только свойств крови пациента, но и, например, измерительной системы. Для повышения надежности требуется реализация некоторого критерия устойчивости используемого маркера. Такой критерий может состоять либо в повторении выхода за границу области зеленых линий хотя бы нескольких красных графиков, отвечающих разным пациентам с установленным диагнозом, либо в сохранении указанного свойства на одном и том же интервале оси абсцисс для локального множества красных кривых, отвечающего повторяющейся группе пациентов, при изменении параметров функции
указанного превышения является своей для каждого красного графика. Это означает слабую достоверность маркера такого рода, поскольку может быть обусловлено случайными флуктуациями не только свойств крови пациента, но и, например, измерительной системы. Для повышения надежности требуется реализация некоторого критерия устойчивости используемого маркера. Такой критерий может состоять либо в повторении выхода за границу области зеленых линий хотя бы нескольких красных графиков, отвечающих разным пациентам с установленным диагнозом, либо в сохранении указанного свойства на одном и том же интервале оси абсцисс для локального множества красных кривых, отвечающего повторяющейся группе пациентов, при изменении параметров функции 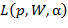 в границах достаточно существенного интервала.
в границах достаточно существенного интервала.
Следовательно, необходимо определить дополнительный признак, позволяющий выделить результаты анализов крови, отвечающих красным кривым на рисунке 2а, из совокупности анализов, соответствующих отсутствию патологии у обследуемых пациентов. С этой целью на рисунке 2б изображены, в частности, зависимости 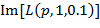 для полной совокупности 32 анализов крови, взятых у здоровых пациентов (зеленые кривые). В силу специфики применяемого математического аппарата, связанной прежде всего с малым числом данных, по которым строится каждый график, при заданных параметрах часть из них полностью совпадает, вследствие чего число зеленых кривых меньше 32. Кроме того, на этом же рисунке приведены те 5 красных графиков, отвечающих установленному ранее диагнозу «шизофрения», которые на рисунке 2а полностью проходят внутри массива зеленых кривых.
для полной совокупности 32 анализов крови, взятых у здоровых пациентов (зеленые кривые). В силу специфики применяемого математического аппарата, связанной прежде всего с малым числом данных, по которым строится каждый график, при заданных параметрах часть из них полностью совпадает, вследствие чего число зеленых кривых меньше 32. Кроме того, на этом же рисунке приведены те 5 красных графиков, отвечающих установленному ранее диагнозу «шизофрения», которые на рисунке 2а полностью проходят внутри массива зеленых кривых.
На данном рисунке три из указанных пяти красных кривых полностью совпадают с зелеными линиями, в то время как две другие, выделенные пунктиром, значительно отклоняются от «зеленого» массива. Такое отклонение имеет место на большом участке оси 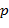 , что свидетельствует об устойчивости данного свойства зависимостей
, что свидетельствует об устойчивости данного свойства зависимостей 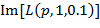 . С учетом этого для констатации высокой вероятности патологии применение неравенства Чебышева здесь не требуется. Таким образом, при прохождении графика функции
. С учетом этого для констатации высокой вероятности патологии применение неравенства Чебышева здесь не требуется. Таким образом, при прохождении графика функции 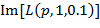 через показанный на рисунке 2б отрезок IJ с вершинами {I (1.000, 0), J(1.500,0)} можем сделать вывод о наличии патологии в организме обследуемого пациента с определенной выше «вероятностью здравого смысла»
через показанный на рисунке 2б отрезок IJ с вершинами {I (1.000, 0), J(1.500,0)} можем сделать вывод о наличии патологии в организме обследуемого пациента с определенной выше «вероятностью здравого смысла» 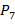 .
.
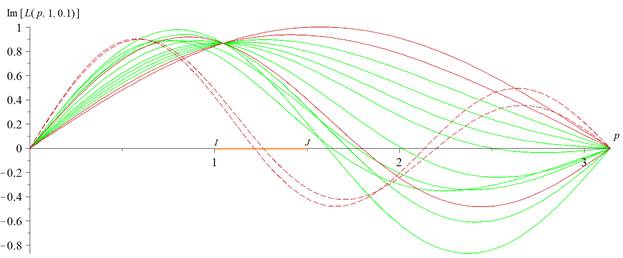
Рис. 2б Сопоставление ансамбля зависимостей 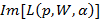 при
при 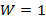 и α=0.1 для здоровых пациентов (зеленые кривые) и пяти красных кривых, которые соответствуют приведенным на рисунке 2а, отвечают установленному диагнозу шизофрении и при этом целиком расположены внутри массива зеленых линий. При заданных параметрах функционала
и α=0.1 для здоровых пациентов (зеленые кривые) и пяти красных кривых, которые соответствуют приведенным на рисунке 2а, отвечают установленному диагнозу шизофрении и при этом целиком расположены внутри массива зеленых линий. При заданных параметрах функционала 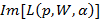 для двух «красных» зависимостей, изображенных пунктиром, удается выделить явный признак отклонения от «зеленого» ансамбля
для двух «красных» зависимостей, изображенных пунктиром, удается выделить явный признак отклонения от «зеленого» ансамбля
На рисунке 3 построены зависимости 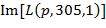 . Здесь три красные линии соответствуют тем трем кривым на рисунке 2б, которые проходят внутри зеленого массива. Как видно из данного рисунка, имеет место одновременный выход значений всей рассматриваемой группы красных линий далеко за пределы ансамбля зеленых линий.
. Здесь три красные линии соответствуют тем трем кривым на рисунке 2б, которые проходят внутри зеленого массива. Как видно из данного рисунка, имеет место одновременный выход значений всей рассматриваемой группы красных линий далеко за пределы ансамбля зеленых линий.
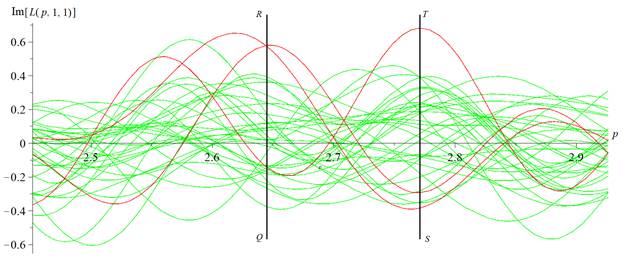
Рис. 3 Сопоставление ансамбля зависимостей 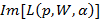 при W=305 и α=1 для здоровых пациентов (зеленые кривые) и трех красных кривых, которые отвечают установленному диагнозу шизофрении и соответствующие которым зависимости на рисунке 2а целиком расположены внутри массива зеленых линий. При заданных параметрах функционала
при W=305 и α=1 для здоровых пациентов (зеленые кривые) и трех красных кривых, которые отвечают установленному диагнозу шизофрении и соответствующие которым зависимости на рисунке 2а целиком расположены внутри массива зеленых линий. При заданных параметрах функционала 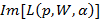 для указанных красных зависимостей удается выделить явный признак отклонения от «зеленого» ансамбля
для указанных красных зависимостей удается выделить явный признак отклонения от «зеленого» ансамбля
С целью дополнительной верификации по аналогии с расчетом для отрезка EF (рис. 1в) при 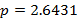 и
и 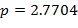 (точки отсчета берутся вдоль вертикальных черных отрезков QR и соответственно ST) согласно (6) был проведен расчет минимальной вероятности патологии для красных кривых, пересекаемых указанными вертикальными линиями. Для данных, отвечающих QR, указанная вероятность составляет 96.3%, а для ST – 96.1%, что вновь близко к вероятности
(точки отсчета берутся вдоль вертикальных черных отрезков QR и соответственно ST) согласно (6) был проведен расчет минимальной вероятности патологии для красных кривых, пересекаемых указанными вертикальными линиями. Для данных, отвечающих QR, указанная вероятность составляет 96.3%, а для ST – 96.1%, что вновь близко к вероятности 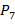 , вычисленной по принципу здравого смысла. Разумеется, недостатком методики, связанной с рисунком 3, является тот факт, что область аргумента
, вычисленной по принципу здравого смысла. Разумеется, недостатком методики, связанной с рисунком 3, является тот факт, что область аргумента 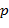 , в которой три рассматриваемые красные кривые принимают значения существенно большие, чем любая зависимость из «зеленого ансамбля», приходится на зону, где полностью отсутствует топологическое подобие линий как зеленого, так и красного ансамблей. Тем не менее сам факт группового выхода на значительном отрезке оси абсцисс (протяженность которого соизмерима с
, в которой три рассматриваемые красные кривые принимают значения существенно большие, чем любая зависимость из «зеленого ансамбля», приходится на зону, где полностью отсутствует топологическое подобие линий как зеленого, так и красного ансамблей. Тем не менее сам факт группового выхода на значительном отрезке оси абсцисс (протяженность которого соизмерима с  ) исследуемой части «красного» ансамбля из зоны зеленых линий, сопровождаемый близкой к единице вероятностью патологии, является аргументом в пользу дополнительного рассмотрения гипотезы о наличии заболевания у соответствующих пациентов.
) исследуемой части «красного» ансамбля из зоны зеленых линий, сопровождаемый близкой к единице вероятностью патологии, является аргументом в пользу дополнительного рассмотрения гипотезы о наличии заболевания у соответствующих пациентов.
Таким образом, приходим к следующему алгоритму определения высокой вероятности заболевания шизофренией по результатам анализа крови пациента.
1. Проверяется, проходит ли отвечающий исследуемому анализу крови график функции 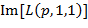 через отрезки AB и (или) CD (рис. 1а и 1б). В первом случае минимальная вероятность заболевания оценивается как
через отрезки AB и (или) CD (рис. 1а и 1б). В первом случае минимальная вероятность заболевания оценивается как 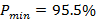 , а во втором, при условии пересечения графиком
, а во втором, при условии пересечения графиком 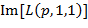 только одного отрезка CD, значение
только одного отрезка CD, значение 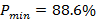 , см. (9) и (10).
, см. (9) и (10).
2. При невыполнении пункта 1 рассматриваемого алгоритма проверяется, имеет ли место прохождение кривой 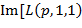 при
при 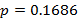 в области
в области 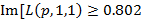 или при
или при 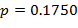 в интервале значений
в интервале значений 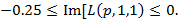 В первом случае
В первом случае 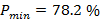 , а в втором
, а в втором 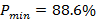 , см. (11) и (12).
, см. (11) и (12).
3. При невыполнении пунктов 1 и 2 проверяется, проходит ли график зависимости 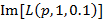 через отрезок IJ (рис. 3). Если это так, то минимальную вероятность патологии принимаем равной вероятности
через отрезок IJ (рис. 3). Если это так, то минимальную вероятность патологии принимаем равной вероятности 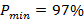 , рассчитываемой по принципу здравого смысла, см. (13).
, рассчитываемой по принципу здравого смысла, см. (13).
4. При наличии предварительно сформулированного врачом предположения о возможности заболевания шизофренией сделанный в пунктах 1–3 вывод может служить серьезным подтверждением высокой вероятности справедливости указанного диагноза.
5. При невыполнении пунктов 1, 2 и 3 проверяется, имеет ли место для каких-либо значений параметров 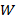 и
и 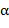 выход значений
выход значений 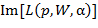 за пределы «зеленого» ансамбля аналогичных кривых, соответствующих нормальному состоянию здоровья. Если указанный выход имеет место в области, где аналогичное свойство проявляется для нескольких графиков рассматриваемых зависимостей, отвечающих установленному диагнозу исследуемого заболевания, причем определенная (по аналогии с расчетами для рисунка 3) на основании неравенства Чебышева вероятность патологии очень близка к единице, то это может рассматриваться как аргумент в пользу гипотезы о наличии рассматриваемого заболевания.
за пределы «зеленого» ансамбля аналогичных кривых, соответствующих нормальному состоянию здоровья. Если указанный выход имеет место в области, где аналогичное свойство проявляется для нескольких графиков рассматриваемых зависимостей, отвечающих установленному диагнозу исследуемого заболевания, причем определенная (по аналогии с расчетами для рисунка 3) на основании неравенства Чебышева вероятность патологии очень близка к единице, то это может рассматриваться как аргумент в пользу гипотезы о наличии рассматриваемого заболевания.
6. Поскольку при вычислении вероятностей с использованием следствия (6) из неравенства Чебышева расчет значения дисперсии 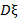 проводился при значении доверительной вероятности
проводился при значении доверительной вероятности 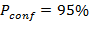 , то имеет смысл обсуждение вопроса о замене более высоких минимальных вероятностей патологии, получаемых при расчетах, на
, то имеет смысл обсуждение вопроса о замене более высоких минимальных вероятностей патологии, получаемых при расчетах, на 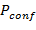 . Вместе с тем сам факт получения указанных вероятностей в диапазоне от
. Вместе с тем сам факт получения указанных вероятностей в диапазоне от 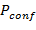 до почти 100% является дополнительным показателем обоснованности применяемой методики.
до почти 100% является дополнительным показателем обоснованности применяемой методики.
Заключение
В случае выявления согласно предлагаемой в статье методике высокой вероятности патологии при исследовании анализа крови у врача появляется возможность дополнительной аргументации ранее выдвинутой гипотезы о наличии психосоматических проблем в состоянии здоровья соответствующего пациента. Проведенные вычисления подтверждают ранее выдвинутое авторами предположение [4] о вполне фиксируемом изменении свойств статистических функционалов, связанных с данными медицинских исследований, при возникновении в работе организма даже малого случайного слагаемого, связанного с воздействием заболевания и в силу этого статистически независимого с нормальной жизнедеятельностью организма. В виде обобщения авторы полагают, что для большого числа видов заболеваний достаточно легко удастся подобрать параметры рассматриваемого математического аппарата, позволяющие разделить ансамбли зависимостей, отвечающие изучаемой патологии и соответственно нормальному состоянию здоровья.



