В настоящее время область строительства представляет собой сложную многообъектную систему, деятельность которой обеспечивается большим количеством человек, технических средств, объектов внешней среды, которые должны действовать во все время меняющихся условиях. Поскольку все перечисленные элементы должны действовать в непрерывной взаимосвязи друг с другом, то необходим аналитический поиск приемлемых условий их взаимодействия. С другой стороны, происходит постоянное усложнение производства строительных материалов и конструкций, что влечет естественное усложнение решаемых при их проектировании задач. Такое усложнение может повлечь рост ошибок при решении подобных задач. Все вышесказанное предполагает использование математических моделей и компьютера для всестороннего анализа объекта строительства. Не является исключением и область материаловедения.
Одним из важнейших инструментов в решении задач строительного материаловедения является математическое моделирование. При этом можно определить следующим образом цель математического программирования при решении данных задач: изучение и анализ свойств и составов материалов, отыскание в них задач, относящихся к оптимизационным, постановка и внедрение которых могут оправдать затраты на создание нового стройматериала в условиях, когда имеют место ограничения технико-экономического или какого-либо другого характера [1; 2].
Широта использования метода наименьших квадратов в различных сферах исследовательских задач не вызывает сомнения. Во многих случаях на практике необходимо получить аппроксимацию данных с помощью возможной зависимости и сделать верные выводы. Стандартным условием данной задачи является следующее: пусть в результате эксперимента получен ряд измерений величины X, соответствующих значениям величины Y, представленные в виде точек (xi , yi), и требуется установить эмпирическую зависимость между Y и X. Данная модель и нашла отражение в задачах строительного материаловедения.
В современном мире математическая задача наиболее интересна и значима, если есть ее компьютерная реализация. Целью нашей работы является реализация метода наименьших квадратов на языке Паскаль в среде программирования Delphi на примерах задач строительного моделирования.
Материалы и методы исследования
Постановка задачи звучит следующим образом. Необходимо установить эмпирическую зависимость 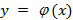 , которая сводится к проведению по данным экспериментальным точкам кривой (ломаная исключается). При этом предполагается, что данная кривая будет проходить как можно ближе к истинной функциональной зависимости y = yu (x). Метод наименьших квадратов и представляет собой согласование кривой
, которая сводится к проведению по данным экспериментальным точкам кривой (ломаная исключается). При этом предполагается, что данная кривая будет проходить как можно ближе к истинной функциональной зависимости y = yu (x). Метод наименьших квадратов и представляет собой согласование кривой 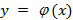 и экспериментальных точек, при котором выполняется данное условие минимизации.
и экспериментальных точек, при котором выполняется данное условие минимизации.
Сглаживание экспериментальных зависимостей по методу наименьших квадратов возможно в виде линейных, квадратичных, экспоненциальных и тригонометрических функций. Все подсчеты коэффициентов в данных экспериментальных зависимостях достаточно громоздки, для эффективности и быстроты результата нами была разработана реализация метода наименьших квадратов на языке Паскаль в среде программирования Delphi, что позволяет видеть оптимальное решение и различные виды аппроксимации [3].
В разработанной программе идет расчет коэффициентов для 4 видов функций: линейная функция; степенная функция; показательная функция и квадратичная функция.
Расчет осуществляется следующим фрагментом программы (представлены фрагменты только для линейной, степенной и показательной функций), фрагменты алгоритма представлены в таблице 1.
Таблица 1
Фрагменты программы с расчетом коэффициентов
|
Вид алгоритма |
Алгоритм |
|
Расчет коэффициентов для линейной функции |
FOR i:= 1 TO 5 do begin u[i]:= x[i]; v[i]:= y[i]; end; s1:=0;s2:=0;s3:=0;s4:=0; FOR i:= 1 TO 5 do begin s1:= s1 + u[i]; s2:= s2 + v[i]; s3:= s3 + u[i] * v[i]; s4:= s4 + u[i]*u[i]; end; d:= 5 * s4 - s1*s1; a:= (5 * s3 - s1 * s2)/d; b:= (s4 * s2 - s1 * s3)/d; |
|
Изображение линейной функции |
res.Caption:='y= '+FloatToStr(a)+'*x + '+FloatToStr(b); s[1]:=0; k:=0; while k<=10 do begin l:=a*k+b; k1:= round((k-minx)*mx+30); l1:= round((miny-l)*my+ny+30); pl1.Canvas.Pixels[k1,l1] := clRed; k:=k+0.01; end; For i:=1 to 5 do begin z:=a*x[i]+b; s[1]:=s[1] + (y[i] - z)*(y[i] - z); end; Label5.Caption:='S1='+FloatToStr(s[1]); |
|
Расчет коэффициентов для степенной функции |
pl2.Canvas.Pen.Color:=CLNavy; for i:=1 to 5 do begin pl2.Canvas.Ellipse(x1[i],y1[i],x1[i]+2,y1[i]+2); end; FOR i:= 1 TO 5 do begin u[i]:= ln(x[i]); v[i]:= ln(y[i]); end; FOR i:= 1 TO 5 do begin s1:= s1 + u[i]; s2:= s2 + v[i]; s3:= s3 + u[i] * v[i]; s4:= s4 + u[i]*u[i]; end; d:= 5 * s4 - s1*s1; a:= (5 * s3 - s1 * s2)/d; b:= (s4 * s2 - s1 * s3)/d; Label2.Caption:='y= '+FloatToStr(exp(b))+'*x^ '+FloatToStr(a); |
|
Изображение степенной функции |
k:=0.01; while k<=10 do begin l:=exp(b)*exp(a*ln(k)); k1:= round((k-minx)*mx+30); l1:= round((miny-l)*my+ny+30); pl2.Canvas.Pixels[k1,l1] := clBlack; k:=k+0.01; end; s[2]:=0; For i:=1 to 5 do begin z:=exp(b)*exp(a*ln(x[i])); s[2]:=s[2] + (y[i] - z)*(y[i] - z); end; Label6.Caption:='S2='+FloatToStr(s[2]); |
|
Расчет коэффициентов для показательной функции |
pl3.Canvas.Pen.Color:=CLNavy; for i:=1 to 5 do begin pl3.Canvas.Ellipse(x1[i],y1[i],x1[i]+2,y1[i]+2); end; s1:=0; s2:=0; s3:=0; s4:=0; FOR i:= 1 TO 5 do begin u[i]:= x[i]; v[i]:= log2(y[i])/log2(exp(1)); end; FOR i:= 1 TO 5 do begin s1:= s1 + u[i]; s2:= s2 + v[i]; s3:= s3 + u[i] * v[i]; s4:= s4 + u[i]*u[i]; end; a:=0; b:=0; d:=0; d:= 5 * s4 - s1*s1; a:= (5 * s3 - s1 * s2)/d; b:= (s4 * s2 - s1 * s3)/d; res2.Caption:='y= '+FloatToStr(exp(b))+'*e^('+FloatToStr(a)+'*x)'; |
|
Изображение показательной функции |
k:=0.01; while k<=10 do begin l:=exp(b)*exp(a*k); k1:= round((k-minx)*mx+30); l1:= round((miny-l)*my+ny+30); pl3.Canvas.Pixels[k1,l1] := clBlue; k:=k+0.01; end; s[3]:=0; For i:=1 to 5 do begin z:=exp(b)*exp(a*x[i]); s[3]:=s[3] + (y[i] - z)*(y[i] - z); end; Label7.Caption:='S3='+FloatToStr(s[3]); |
Также осуществляется выбор наилучшего приближения.
//рисуем лучший график
lk:=1;
for i:=1 to 4 do
if s[i]<s[lk] then lk:=i; res4.Caption:=FloatToStr(s[lk]);
//ВЫБОР
case lk of
1: begin
FOR i:= 1 TO 5 do begin u[i]:= x[i]; v[i]:= y[i]; end;
s1:=0;s2:=0;s3:=0;s4:=0;
FOR i:= 1 TO 5 do begin
s1:= s1 + u[i]; s2:= s2 + v[i]; s3:= s3 + u[i] * v[i]; s4:= s4 + u[i]*u[i];
end;
d:= 5 * s4 - s1*s1; a:= (5 * s3 - s1 * s2)/d; b:= (s4 * s2 - s1 * s3)/d;
//рисуем график лин/ф
k:=0;
while k<=10 do begin
l:=a*k+b; k1:= round((k-minx)*mx+50); l1:= round((miny-l)*my+ny+50);
pl.Canvas.Pixels[k1,l1] := clRed; k:=k+0.01;
end;
res5.Caption:='Линейная функция';
end;
2: begin
FOR i:= 1 TO 5 do begin u[i]:= ln(x[i]); v[i]:= ln(y[i]); end;
s1:=0;s2:=0;s3:=0;s4:=0;
FOR i:= 1 TO 5 do begin
s1:= s1 + u[i]; s2:= s2 + v[i]; s3:= s3 + u[i] * v[i]; s4:= s4 + u[i]*u[i];
end;
d:= 5 * s4 - s1*s1; a:= (5 * s3 - s1 * s2)/d; b:= (s4 * s2 - s1 * s3)/d;
и т.д.
Вид программы приведен на рисунке 1.
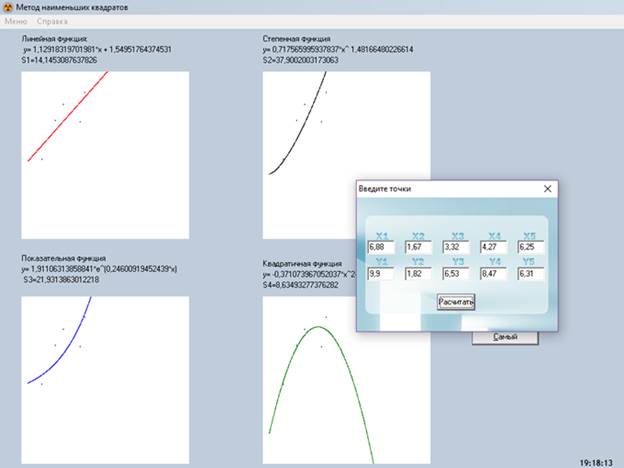
Рис. 1. Визуализация программы
Результаты исследования и их обсуждение
Данная программа была предложена студентам строительных специальностей, обучающимся в Пензенском государственном университете архитектуры и строительства. Существуют и другие программные средства, в которых может быть рассчитана аппроксимация функции методом МНК, например математические пакеты MathCAD, MathLab, но их использование требует от студентов знаний основ программирования для реализации алгоритмов. Поэтому преимущество использования разработанной нами программы несомненно.
Рассмотрим расчет параметров, необходимых в задачах строительного материаловедения [4-6].
Пример. По результатам исследований необходимо установить связи между коэффициентами пластичности (kпл) и структуры (kстр) эпоксидных композитов, представленных в таблице 1, определить параметры 4 видов функций и выбрать оптимальный результат [1] (табл. 2).
Таблица 2
|
xi |
6,88 |
1,67 |
3,32 |
4,27 |
6,25 |
|
yi |
9,9 |
1,82 |
6,53 |
8,47 |
6,31 |
Программа выдаёт следующие результаты (рис. 2).
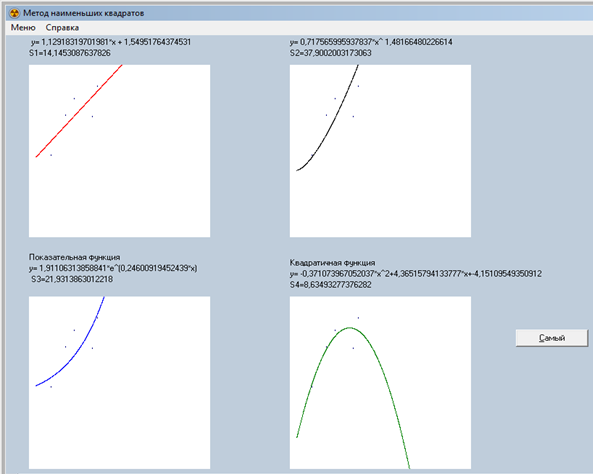
Рис. 2. Результаты решения
Наилучшим приближением является квадратичная функция (рис. 3).
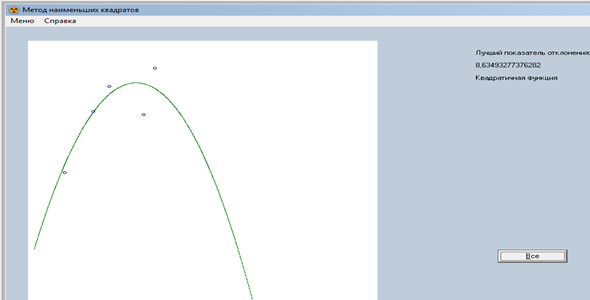
Рис. 3. Наилучший вариант аппроксимации МНК
Пример: зависимость вязкости эпоксидных композитов B от температуры t, °C, при 5%-ной концентрации машинного масла приводится в таблице 3.
Таблица 3
|
xi = ti, °C |
10 |
10,3 |
10,4 |
10,55 |
10,6 |
|
yi = Bi |
12,1 |
12,6 |
13 |
13,8 |
14,9 |
Определить параметры 4 видов зависимостей и выбрать оптимальную (рис. 4).
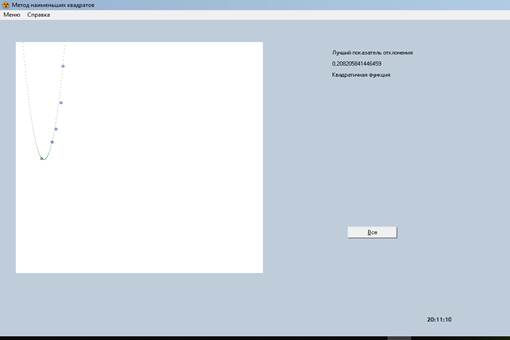
Рис. 4. Оптимальное решение
Выводы
Из демонстрационных примеров, их наглядной представленности видно, что разработанная программа является удобным и наглядным средством в решении технических задач с использованием МНК. Программа не требует от студентов знаний основ программирования, по сравнению с другими программными средствами. Может быть использована при решении задач строительного характера пользователями с любым уровнем ИКТ-компетенций.



